引力波天文系列文章将介绍引力波能观测到什么，如何观测，以及基本的数据分析方法。侧重于引力波的空间探测和分析，但核心的测量原理、仪器响应以及数据分析方法基本都是通用的。
本文介绍引力波的空间探测技术。
空间观测概述
相关项目介绍
低频引力波
主流mHZ频段
https://en.wikipedia.org/wiki/Laser_Interferometer_Space_Antenna#History
三臂、500万公里
Pathfinder 2015年12月3日发射
地月距离36-40万公里，LISA/Taiji臂长约地月距离的10倍，天琴臂长约地月距离的一半。
其它频段项目
卫星轨道简介
无拖曳卫星编队 (satellite formation)目标载荷 (测试质量)不受引力之外的其它力作用的卫星。为实现该目标，卫星会将检验质量或测试质量(proof mass)置于真空壳层内，测试质量在壳层内自由悬浮，并实时监测其与外壁的距离。任何距离的改变都代表卫星受到了非重力因素影响，相对测试质量出现了运动位移，卫星会启动微推进器做出补偿调整，恢复两者相对位置。在外壳的保护下，太阳风、光压等非重力因素的影响被屏蔽，测试质量仅在重力作用下沿测地线运动。而通过追踪测试质量，卫星本身运动也始终追随测地线。
惯性传感器+微推进系统 ，其中惯性传感系统被称为重力参考传感器GRS(Gravitational Reference Sensor)，包括测试质量+电极室+真空室及相关传感器。
无拖曳卫星需对测试质量在三个方向的平移及旋转，共计六个自由度上，对测试质量实现追踪。但对三臂的空间干涉阵而言，每颗卫星都有两个测试质量，分别用于与其余两颗卫星进行连接。显然卫星无法在所有自由度上同时对两者保持追踪，因此实际中，只会在与其它卫星连接的视线方向上保持测试质量完全自由。即对每个测试质量只在一个方向保持追踪，其余自由度全部由电容制动装置加以控制。若两个追踪方向相互正交相对易理解，追踪60°夹角的两个方向虽然不直观，但仍是可行的。
对于LISA而言，测试质量的精度可达到3 × 1 0 − 15 m / s 2 / H z 1 / 2 3\times 10^{-15}\rm m/s^2/{Hz}^{1/2} 3 × 1 0 − 1 5 m / s 2 / H z 1 / 2 1 m H z 1{\rm mHz} 1 m H z
最简单的想法是类似地面，由同一光源分光后经过不同路径反射回本地干涉，但对于卫星干涉测量：
一方面，数千至数百万公里以上的臂长，意味激光强度衰减严重，通过反射往返测量不现实。以LISA为例，取激光出射功率为1W，激光接受功率仅约250pW，有近10个量级的衰减。因此，实际中会采用单程测量，即各卫星分别用本地激光指向其它卫星，三臂往返一共六路激光测量数据。
另一方面，三个卫星各自独立控制，考虑到月球及其它行星的引力作用，卫星的臂长在不断波动(“呼吸”)，测试质量间存在相对运动。这会导致：
不同卫星间臂长不相等。以LISA为例，臂长波动在1%量级，即几万公里的相对位移。激光频率的不稳定性在1Hz、kHz、MHz量级？
卫星间往返路径不相等，除了不同卫星间
测试质量间存在相对运动，引入激光频率的多普勒偏移。
由同一光源分光经过相同长度的路径后自动干涉，无需考虑频率波动、无需测量初始相位。
考虑到
臂长不相等：时间延迟干涉技术
存在多普勒效应：外差干涉测量
空间引力波每条路径的光束与标准的参考激光对比，精确记录各自的相位，一共记录三臂往返的六路激光数据。不同路径的激光干涉是在数据(预)处理阶段离线进行。因为探测器响应记录到的是每路激光的相位延迟，并未直接提供不同路径光的干涉信息。
事实上，每路激光数据也是由三个干涉器共同完成测量。
通过轨道的合理设置，星间距离保持稳定。忽略干扰因素，三颗卫星各自沿测底线做开普勒运动，轨道平面与黄道面夹角一致，但升交点依次相错2 π 3 \frac{2\pi}{3} 3 2 π
三颗卫星的中心位于黄道面，沿地球轨道以年为周期公转，与地球保持约20°；
三颗卫星构成的平面公转过程中始终面向太阳，与黄道面保持约60°倾斜；
三颗卫星保持60°夹角/等边三角形，整体在卫星平面中绕中心以年为周期(反向)“自转”；
但实际中，会受到各种扰动
臂长存在约2%的波动(5万公里)，非等臂干涉激光自身频率噪声无法在干涉测量时直接抵消
臂长波动对应卫星视向相对速度约10m/s，激光频率偏移不再适用零差干涉，需用外差干涉
臂长波动意味不再保持等边，卫星夹角将偏离60°，偏差在1°左右，激光指向需相应进行调整
数据链路简介
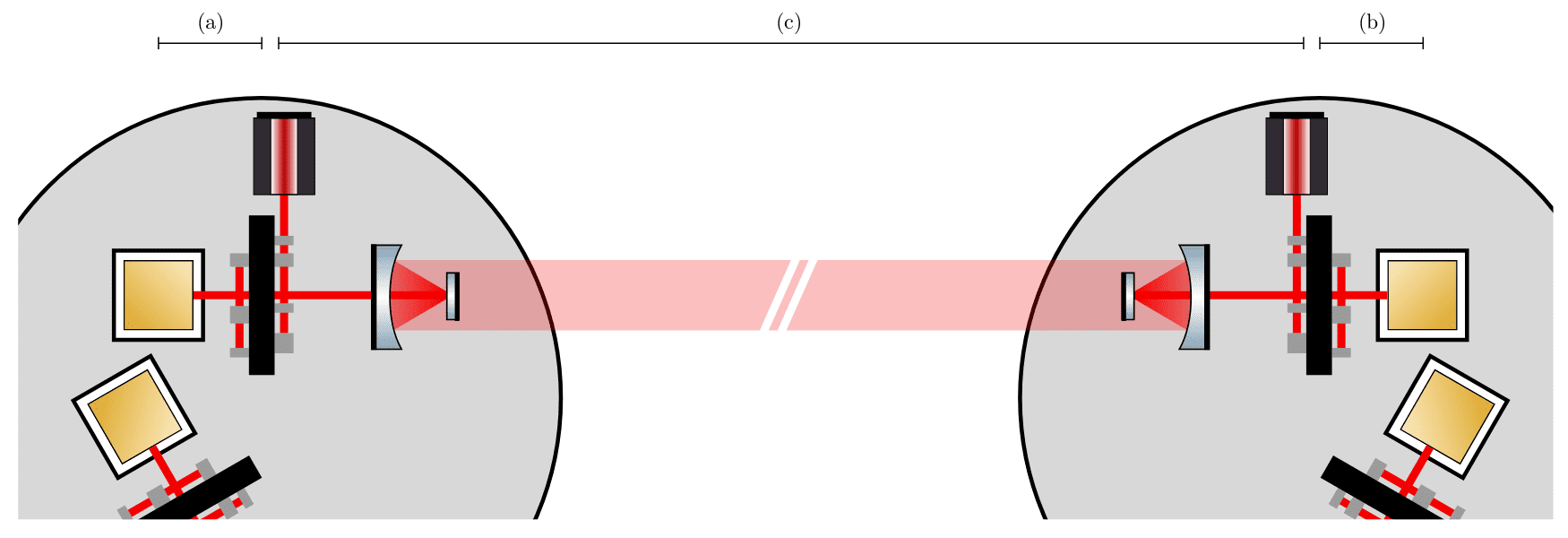
最直观的想法是激光在测试质量上反射后干涉，这也确实是上世纪LISA最初提出时的设计方案，但之后在2005年左右切换为现在的分立干涉(split interferometry)的方案，即将测试质量到测试质量的距离测量拆分为测试质量到光学平台、光学平台到光学平台、光学平台到测试质量三部分，如下图所示，注意与干涉测量中的分光(split)区分。
每颗卫星上有两个科学单元，如下图所示，每个单元的主要组件有：
1个测试质量，位于惯性传感器(重力参考传感器)内部
1个激光系统，红外1064nm Nd:YAG 稳频稳功率激光
1个望远镜，用于发射和接受激光光束，口径30cm
1个光学平台，位于望远镜与GRS之间，承载干涉光路
科学单元正式名称为可动光学子组件(Movable Optical Sub-Assembly, MOSA)，每个组件包含一个望远镜、一个光学平台(Optical Bench, OB)以及一个重力参考传感器(Gravitational Reference Sensor, GRS)，GRS内部则是自由悬浮的测试质量(Test Mass, TM)。
测试质量悬浮于电容电极室(capacitive electrode housing)，通过电容实时监测测试其位置，并通过DFACS()系统实现现卫星的无拖曳控制
重力参考传感器GRS通过激光？/真空室电容？对测试质量位置进行监测，实现卫星的无拖曳控制。每颗卫星上的两个科学单元固定在同一支架上，各自有±1°的旋转自由，用于卫星漂移时保持激光指向对齐。两个科学单元的光学平台之间由光纤连接，用于两个本地激光之间的干涉。光学平台上共有3个光电探测器，分别监测3路干涉拍频信号，经低通滤波和ADC转换后由相位计读取相位。
载荷概念设计，两个科学单元挂载在同一支架，呈60°夹角(Amaro-Seoane et al. 2017)
GRS与DFACS连接
每个科学单元(光学平台)的3个光电探测器分别用于三个干涉测量：
分立干涉光路简化示意图，主要包含科学干涉、参考干涉及测试质量干涉
科学干涉：本地激光与远程激光干涉，含GW信息
参考干涉：本地激光与相邻光学平台的激光干涉
本地干涉：本地激光经TM反射后与相邻激光干涉
其中科学干涉用于光学平台到光学平台测距，光学平台到测试质量的距离可通过对比参考干涉和本地干涉得到，两者结合最终实现测试质量到测试质量的测距。此外，为实现干涉测量需要在相邻的本地激光信号间建立关联，以构建干涉环路，这同样依赖参考干涉。作为对比，早期的两路干涉光路设计为：
主要区别在于本地干涉与科学干涉合并，远程激光会直接在测试质量上反射。这里科学干涉测量的是光学平台到测试质量的距离，仍需要参考干涉辅助实现测试质量到测试质量的距离测量。
参考干涉测量的作用：
与本地干涉测量对比抵消噪声，获取光学平台相对于测试质量的位移，即光学平台的位移噪声
通过双向参考干涉与科学干涉测量对比，实现科学数据中本地与相邻激光频率噪声的转换
前面一点也就是在全部六个激光之间的实现锁相
科学干涉，也称星间干涉(Interspacecraft Interferometer, ISI)，包含本地及远程的激光频率噪声，两个光学平台位移噪声，引力波信息以及读出噪声。参考干涉(Reference Interferometer, RFI)包含两个本地激光频率噪声、连接连个光学平台的光纤所引入的相位延迟以及读出噪声。本地干涉，也称测试质量干涉(Test-mass Interferometer, TMI)，包含两个本地激光频率噪声，光纤相位延迟、光学平台的位移噪声、测试质量的加速噪声及读出噪声。这些就是空间引力观测所涉及的主要噪声，除此之外，星间信息传递(频率同步)时信息失真对应于调制噪声，相位计读出采样时还会引入时钟噪声，这里暂不考虑。
所有其它噪声如时钟噪声或指向噪声的效应都要在TDI之后才能显现，相应的噪声抑制或修正也都建立在TDI的输出之上，而TDI本身又可能对这些噪声产生影响。
其它噪声
指向噪声
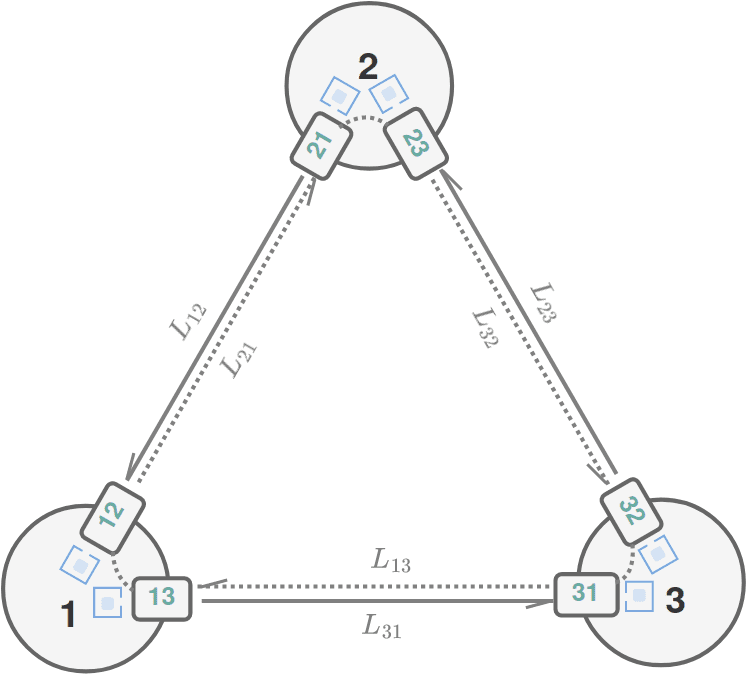
为使用数学符号表示，首先对标号做出约定：
这里采用LISA项目的最新记号规则(Hartwig et al. 2021, Bayle et al. 2021)。如上图所示，卫星沿顺时针依次记为1、2、3；卫星上的科学单元用两个下标指示，前者对应所在卫星，后者对应所指向的卫星；连接臂标号与其所指向的科学单元一致，沿其传播的激光最终会在对应科学单元上进行干涉。
以s ( t ) , ε ( t ) , τ ( t ) s(t), \varepsilon(t), \tau(t) s ( t ) , ε ( t ) , τ ( t )
s 12 ( t ) = p 21 ( t − L 12 / c ) − p 12 ( t ) − 2 π ν 21 Δ 21 ( t − L 12 / c ) − Δ 12 ( t ) c + H 12 ( t ) + N 12 s ( t ) ε 12 ( t ) = p 13 ( t ) − p 12 ( t ) − 2 × 2 π ν 13 δ 12 ( t ) − Δ 12 ( t ) c + μ 12 ( t ) + N 12 ε ( t ) τ 12 ( t ) = p 13 ( t ) − p 12 ( t ) + μ 12 ( t ) + N 12 τ ( t ) \begin{aligned}
s_{12}(t) &= p_{21}(t-L_{12}/c) - p_{12}(t) - 2\pi\nu_{21}{\small \frac{\Delta_{21}(t-L_{12}/c) - \Delta_{12}(t)}{c}} + H_{12}(t) + N_{12}^{s}(t) \\
\varepsilon_{12}(t) &= p_{13}(t) - p_{12}(t) - 2{\small~\times~} 2\pi\nu_{13}{\small \frac{\delta_{12}(t) - \Delta_{12}(t)}{c}} + \mu_{12}(t) + N_{12}^{\varepsilon}(t)\\
\tau_{12}(t) &= p_{13}(t) - p_{12}(t) + \mu_{12}(t) + N_{12}^{\tau}(t)\\
\end{aligned} s 1 2 ( t ) ε 1 2 ( t ) τ 1 2 ( t ) = p 2 1 ( t − L 1 2 / c ) − p 1 2 ( t ) − 2 π ν 2 1 c Δ 2 1 ( t − L 1 2 / c ) − Δ 1 2 ( t ) + H 1 2 ( t ) + N 1 2 s ( t ) = p 1 3 ( t ) − p 1 2 ( t ) − 2 × 2 π ν 1 3 c δ 1 2 ( t ) − Δ 1 2 ( t ) + μ 1 2 ( t ) + N 1 2 ε ( t ) = p 1 3 ( t ) − p 1 2 ( t ) + μ 1 2 ( t ) + N 1 2 τ ( t )
其中p ( t ) p(t) p ( t ) ν \nu ν Δ ( t ) \Delta(t) Δ ( t ) δ ( t ) \delta(t) δ ( t ) H ( t ) H(t) H ( t ) N ( t ) N(t) N ( t ) μ ( t ) \mu(t) μ ( t )
注意，参考干涉中的位移项δ 12 ( t ) − Δ 12 ( t ) c \frac{\delta_{12}(t) - \Delta_{12}(t)}{c} c δ 1 2 ( t ) − Δ 1 2 ( t ) p 12 p_{12} p 1 2 p 13 p_{13} p 1 3
引入沿激光臂方向的延时算符及单位矢量，上述公式可简记为：
s 12 = D 12 p 21 − p 12 − 2 π ν 21 n ^ 12 c ⋅ ( D 12 Δ 21 − Δ 12 ) + H 12 + N 12 s ε 12 = p 13 − p 12 − 2 × 2 π ν 13 n ^ 12 c ⋅ ( δ 12 − Δ 12 ) + μ 12 + N 12 ε τ 12 = p 13 − p 12 + μ 12 + N 12 τ \begin{aligned}
s_{12} &= \mathcal{D}_{12} p_{21} - p_{12} - 2\pi\nu_{21} \frac{\hat{\bm{n}}_{12}}{c} \cdot (\mathcal{D}_{12} \bm{\Delta}_{21} - \bm{\Delta}_{12}) + H_{12} + N_{12}^{s}\\
\varepsilon_{12} &= p_{13} - p_{12} - 2{\small~\times~} 2\pi\nu_{13}\frac{\hat{\bm{n}}_{12}}{c} \cdot (\bm{\delta}_{12} - \bm{\Delta}_{12}) + \mu_{12} + N_{12}^{\varepsilon}\\
\tau_{12} &= p_{13} - p_{12} + \mu_{12} + N_{12}^{\tau}
\end{aligned} s 1 2 ε 1 2 τ 1 2 = D 1 2 p 2 1 − p 1 2 − 2 π ν 2 1 c n ^ 1 2 ⋅ ( D 1 2 Δ 2 1 − Δ 1 2 ) + H 1 2 + N 1 2 s = p 1 3 − p 1 2 − 2 × 2 π ν 1 3 c n ^ 1 2 ⋅ ( δ 1 2 − Δ 1 2 ) + μ 1 2 + N 1 2 ε = p 1 3 − p 1 2 + μ 1 2 + N 1 2 τ
ϕ s c i 12 = D 12 p 21 − p 12 − 2 π ν 21 n ^ 12 c ⋅ ( D 12 Δ 21 − Δ 12 ) + H 12 + N 12 s ϕ l o c 12 = p 13 − p 12 − 2 × 2 π ν 13 n ^ 12 c ⋅ ( δ 12 − Δ 12 ) + μ 12 + N 12 ε ϕ r e f 12 = p 13 − p 12 + μ 12 + N 12 τ \begin{aligned}
\phi_{ {\rm sci}_{12} } &= \mathcal{D}_{12} p_{21} - p_{12} - 2\pi\nu_{21} \frac{\hat{\bm{n}}_{12}}{c} \cdot (\mathcal{D}_{12} \bm{\Delta}_{21} - \bm{\Delta}_{12}) + H_{12} + N_{12}^{s}\\
\phi_{ {\rm loc}_{12} } &= p_{13} - p_{12} - 2{\small~\times~} 2\pi\nu_{13}\frac{\hat{\bm{n}}_{12}}{c} \cdot (\bm{\delta}_{12} - \bm{\Delta}_{12}) + \mu_{12} + N_{12}^{\varepsilon}\\
\phi_{ {\rm ref}_{12} } &= p_{13} - p_{12} + \mu_{12} + N_{12}^{\tau}
\end{aligned} ϕ s c i 1 2 ϕ l o c 1 2 ϕ r e f 1 2 = D 1 2 p 2 1 − p 1 2 − 2 π ν 2 1 c n ^ 1 2 ⋅ ( D 1 2 Δ 2 1 − Δ 1 2 ) + H 1 2 + N 1 2 s = p 1 3 − p 1 2 − 2 × 2 π ν 1 3 c n ^ 1 2 ⋅ ( δ 1 2 − Δ 1 2 ) + μ 1 2 + N 1 2 ε = p 1 3 − p 1 2 + μ 1 2 + N 1 2 τ
s 12 = D 12 p 21 − p 12 − 2 π ν 21 n ^ 12 c ⋅ ( D 12 Δ 21 − Δ 12 ) + H 12 + ν b e a t + N 12 s ε 12 = p 13 − p 12 − 2 × 2 π ν 13 n ^ 12 c ⋅ ( δ 12 − Δ 12 ) + μ 12 + N 12 ε τ 12 = p 13 − p 12 + μ 12 + N 12 τ \begin{aligned}
s_{12} &= \mathcal{D}_{12} p_{21} - p_{12} - 2\pi\nu_{21} \frac{\hat{\bm{n}}_{12}}{c} \cdot (\mathcal{D}_{12} \bm{\Delta}_{21} - \bm{\Delta}_{12}) + H_{12} + \frac{\nu_{\rm beat}}{} + N_{12}^{s}\\
\varepsilon_{12} &= p_{13} - p_{12} - 2{\small~\times~} 2\pi\nu_{13}\frac{\hat{\bm{n}}_{12}}{c} \cdot (\bm{\delta}_{12} - \bm{\Delta}_{12}) + \mu_{12} + N_{12}^{\varepsilon}\\
\tau_{12} &= p_{13} - p_{12} + \mu_{12} + N_{12}^{\tau}\\
\end{aligned} s 1 2 ε 1 2 τ 1 2 = D 1 2 p 2 1 − p 1 2 − 2 π ν 2 1 c n ^ 1 2 ⋅ ( D 1 2 Δ 2 1 − Δ 1 2 ) + H 1 2 + ν b e a t + N 1 2 s = p 1 3 − p 1 2 − 2 × 2 π ν 1 3 c n ^ 1 2 ⋅ ( δ 1 2 − Δ 1 2 ) + μ 1 2 + N 1 2 ε = p 1 3 − p 1 2 + μ 1 2 + N 1 2 τ
在TDI分析中会通过延时操作构建虚拟等臂干涉，在这一过程通常默认每颗卫星上只有一个激光噪声源。而上述干涉测量涉及六路激光，需要消除其中三个，得到等效的分光干涉测量，每颗卫星只有一个激光。
中间变量，这是后续TDI分析的基础。
η 12 = \begin{aligned}
\eta_{12} &= \\
\end{aligned} η 1 2 =
注意，科学干涉中本地激光在W量级，而远程激光仅0.1nW量级，约10个量级的差别；参考及本地干涉中的相邻激光也只有mW量级。此外参考干涉是双向的：当前科学单元的本地激光会与经光纤过来的相邻科学单元激光干涉，相邻科学单元的激光与会经光纤过去的本地激光干涉作为参考干涉。假设光纤的相位延迟是对易的，即从左向右传播与从右向左传播的相位延迟相等，则双向参考干涉相减，光纤噪声抵消，可得到两个科学单元激光相位(频率噪声)间的关联。
TDI 技术需要高精度的绝对距离数据。结合激光相位伪码调制，LISA 的 TDI 系统需在 5x106 km 臂长下实现绝对距离测量精度 30cm-11 量级？引力波在pm量级？？？
在空间引力波探测中，两卫星之间最大速度约为 10m/s，对应相位计带宽范围约是 2MHz~25MHz，pm量级测量要求鉴相精度达到一个圆周的一百万分之一
涉及到的物理量之间的转换
E ( t ) = E 0 ( t ) e j φ ( t ) = E 0 ( t ) e j [ 2 π ν 0 t + ϕ ( t ) ] E(t) = E_0(t) e^{j\varphi(t)} = E_0(t) e^{j[2\pi\nu_0 t + \phi(t)]}
E ( t ) = E 0 ( t ) e j φ ( t ) = E 0 ( t ) e j [ 2 π ν 0 t + ϕ ( t ) ]
这里E 0 ( t ) E_0(t) E 0 ( t ) φ ( t ) \varphi(t) φ ( t ) 角 频率。ν 0 \nu_0 ν 0 ϕ ( t ) \phi(t) ϕ ( t ) φ ( t ) \varphi(t) φ ( t ) 2 π ν 0 t 2\pi\nu_0 t 2 π ν 0 t ϕ ( t ) \phi(t) ϕ ( t )
ω ( t ) = φ ˙ ( t ) , ν ( t ) = φ ˙ ( t ) 2 π = ν 0 + ϕ ˙ ( t ) 2 π ; φ ( t ) = 2 π ∫ t 0 t ν ( τ ) d τ \omega(t) = \dot{\varphi}(t), ~~~ \nu(t) = \frac{\dot{\varphi}(t)}{2\pi} = \nu_0 + \frac{\dot{\phi}(t)}{2\pi}; ~~~ \varphi(t) = 2\pi \int_{t_0}^t\nu(\tau)d\tau
ω ( t ) = φ ˙ ( t ) , ν ( t ) = 2 π φ ˙ ( t ) = ν 0 + 2 π ϕ ˙ ( t ) ; φ ( t ) = 2 π ∫ t 0 t ν ( τ ) d τ
除了相位与频率外，另两个常用的描述相位演化的物理量是计时抖动(timing jitter)x ( t ) x(t) x ( t ) y ( t ) y(t) y ( t ) ν 0 \nu_0 ν 0 ϕ ( t ) \phi(t) ϕ ( t ) φ ( t ) \varphi(t) φ ( t ) ν ( t ) \nu(t) ν ( t ) ν 0 \nu_0 ν 0
x ( t ) = ϕ ( t ) 2 π ν 0 = φ ( t ) 2 π ν 0 − t ; y ( t ) = x ˙ ( t ) = ν ( t ) − ν 0 ν 0 x(t) = \frac{\phi(t)}{2\pi\nu_0} = \frac{\varphi(t)}{2\pi\nu_0} - t; ~~~~~ y(t) = \dot{x}(t) = \frac{\nu(t)-\nu_0}{\nu_0}
x ( t ) = 2 π ν 0 ϕ ( t ) = 2 π ν 0 φ ( t ) − t ; y ( t ) = x ˙ ( t ) = ν 0 ν ( t ) − ν 0
在激光的接收端，考虑到信号的衰减及时延：
E r e c v ( t ) = E 0 r e c v ( t ) e j [ 2 π ν 0 t + ϕ r e c v ( t ) ] = ρ E e m i t ( t − L / c ) E^{\rm recv}(t) = E^{\rm recv}_0(t) e^{j[2\pi\nu_0 t + \phi^{\rm recv}(t)]} = \rho E^{\rm emit}(t - L/c)
E r e c v ( t ) = E 0 r e c v ( t ) e j [ 2 π ν 0 t + ϕ r e c v ( t ) ] = ρ E e m i t ( t − L / c )
ϕ r e c v ( t ) = ϕ ( t − L / c ) − 2 π ν 0 L / c ; E 0 r e c v ( t ) = ρ E 0 ( t ) \phi^{\rm recv}(t) = \phi(t - L/c) - 2\pi\nu_0 L/c; ~~~~~ E^{\rm recv}_0(t) = \rho E_0(t)
ϕ r e c v ( t ) = ϕ ( t − L / c ) − 2 π ν 0 L / c ; E 0 r e c v ( t ) = ρ E 0 ( t )
y r e c v ( t ) = ϕ ˙ r e c v ( t ) 2 π ν 0 = ϕ ˙ ( t − L c ) 2 π ν 0 ( 1 − L ˙ ( t ) / c ) − L ˙ ( t ) c = ϕ ˙ ( t − L c ) 2 π ν 0 − ( 1 + ϕ ˙ ( t − L c ) 2 π ν 0 ) L ˙ ( t ) c = y ( t − L / c ) − [ 1 + y ( t − L / c ) ] L ˙ ( t ) c \begin{aligned}
y^{\rm recv}(t) = ~&~ \frac{\dot{\phi}^{\rm recv}(t)}{2\pi\nu_0} = \frac{\dot{\phi}(t-\frac{L}{c})}{2\pi\nu_0}\left(1-\dot{L}(t)/c\right) - \frac{\dot{L}(t)}{c}\\
= ~&~ \frac{\dot{\phi}(t-\frac{L}{c})}{2\pi\nu_0} - \left(1 + \frac{\dot{\phi}(t-\frac{L}{c})}{2\pi\nu_0}\right)\frac{\dot{L}(t)}{c}\\
= ~&~ y(t-L/c) - \left[1 + y(t-L/c)\right]\frac{\dot{L}(t)}{c}
\end{aligned} y r e c v ( t ) = = = 2 π ν 0 ϕ ˙ r e c v ( t ) = 2 π ν 0 ϕ ˙ ( t − c L ) ( 1 − L ˙ ( t ) / c ) − c L ˙ ( t ) 2 π ν 0 ϕ ˙ ( t − c L ) − ( 1 + 2 π ν 0 ϕ ˙ ( t − c L ) ) c L ˙ ( t ) y ( t − L / c ) − [ 1 + y ( t − L / c ) ] c L ˙ ( t )
这里考虑了臂长的变化，第一项为发射端激光本身的相对频率波动，后一项为臂长变化所引入的相对频移，对应实际的多普勒效应。注意多普勒效应源于L ˙ \dot{L} L ˙ ϕ r e c v ( t ) \phi^{\rm recv}(t) ϕ r e c v ( t ) ν r e c v ( t ) \nu^{\rm recv}(t) ν r e c v ( t ) y ( t ) y(t) y ( t ) ∼ 10 m / s \sim 10 \rm m/s ∼ 1 0 m / s L ˙ / c ∼ 3 × 1 0 − 8 ≪ 1 , y ( t ) ≪ 1 \dot{L}/c \sim 3\times 10^{-8}\ll 1, ~y(t) \ll 1 L ˙ / c ∼ 3 × 1 0 − 8 ≪ 1 , y ( t ) ≪ 1
y r e c v ( t ) = y ( t − L / c ) − L ˙ ( t ) c y^{\rm recv}(t) = y(t-L/c) - \frac{\dot{L}(t)}{c}
y r e c v ( t ) = y ( t − L / c ) − c L ˙ ( t )
卫星的相对速度是10m/s，还是1m/s？L ˙ ( t ) c \frac{\dot{L}(t)}{c} c L ˙ ( t ) δ ν ∼ 1 H z , y ( t ) ∼ 1 0 − 15 ≪ L ˙ c ; δ ν ∼ 10 M H z , y ( t ) ∼ 3 × 1 0 − 8 ∼ L ˙ c \delta \nu \sim 1{\rm Hz}, y(t) \sim 10^{-15} \ll \frac{\dot{L}}{c}; \delta \nu \sim 10{\rm MHz}, y(t) \sim 3\times10^{-8} \sim \frac{\dot{L}}{c} δ ν ∼ 1 H z , y ( t ) ∼ 1 0 − 1 5 ≪ c L ˙ ; δ ν ∼ 1 0 M H z , y ( t ) ∼ 3 × 1 0 − 8 ∼ c L ˙
外差测量E 1 ( t ) e j π / 2 + E 2 ( t ) E_1(t)e^{j\pi/2} + E_2(t) E 1 ( t ) e j π / 2 + E 2 ( t ) p i / 2 pi/2 p i / 2
E 1 ( t ) + E 2 ( t ) E_1(t) + E_2(t) E 1 ( t ) + E 2 ( t )
I ∝ 1 + 2 E 1 , 0 E 2 , 0 E 1 , 0 2 + E 2 , 0 2 cos [ 2 π ( ν 1 − ν 2 ) t + ϕ 1 ( t ) − ϕ 2 ( t ) ] I \propto 1 + \frac{2 E_{1, 0}E_{2, 0}}{E^2_{1, 0} + E^2_{2, 0}} \cos[2\pi(\nu_1-\nu_2)t + \phi_1(t)-\phi_2(t)]
I ∝ 1 + E 1 , 0 2 + E 2 , 0 2 2 E 1 , 0 E 2 , 0 cos [ 2 π ( ν 1 − ν 2 ) t + ϕ 1 ( t ) − ϕ 2 ( t ) ]
ν 12 = ν 1 − ν 2 , ϕ 12 = ϕ 1 ( t ) − ϕ 2 ( t ) \nu_{12} = \nu_1 - \nu_2, ~~~ \phi_{12} = \phi_1(t) - \phi_2(t)
ν 1 2 = ν 1 − ν 2 , ϕ 1 2 = ϕ 1 ( t ) − ϕ 2 ( t )
y 12 = ϕ ˙ 12 2 π ν 0 = y 1 ( t ) − y 2 ( t ) y_{12} = \frac{\dot{\phi}_{12}}{2\pi\nu_0} = y_1(t) - y_2(t)
y 1 2 = 2 π ν 0 ϕ ˙ 1 2 = y 1 ( t ) − y 2 ( t )
引力波频率用f f f ν \nu ν
引力波信号对于天线臂长(卫星间距离)的扰动可表示为：
h ( t ) = h + S S B ξ + ( u , v , n ) + h × S S B ξ × ( u , v , n ) h(t) = h^{\rm \tiny SSB}_+ \xi_+(\bm{u}, \bm{v}, \bm{n}) + h^{\rm \tiny SSB}_× \xi_×(\bm{u}, \bm{v}, \bm{n})
h ( t ) = h + S S B ξ + ( u , v , n ) + h × S S B ξ × ( u , v , n )
其中h + S S B , h × S S B h^{\rm \tiny SSB}_+, h^{\rm \tiny SSB}_× h + S S B , h × S S B ξ + , ξ × \xi_+, \xi_× ξ + , ξ ×
t 1 ≈ t 0 + L c − 1 2 c ∫ 0 L H ( t 0 − k ⋅ x 0 ( t 0 ) c + 1 − k ⋅ n ^ c x ) d x t_1 \approx t_0 + \frac{L}{c} - \frac{1}{2c} \int_0^L H\left(t_0 - \frac{\bm{k}\cdot\bm{x}_0(t_0)}{c} + \frac{1-\bm{k}\cdot\bm{\hat{n}}}{c} x \right) d x
t 1 ≈ t 0 + c L − 2 c 1 ∫ 0 L H ( t 0 − c k ⋅ x 0 ( t 0 ) + c 1 − k ⋅ n ^ x ) d x
y G W ( t 0 ) ≈ 1 2 k ⋅ n ^ [ H ( t 0 − k ⋅ x 0 ( t 0 ) c ) − H ( t 0 − k ⋅ x 1 ( t 1 ) c + L c ) ] y^{\rm GW}(t_0) \approx \frac{1}{2\bm{k}\cdot\hat{\bm{n}}}\left[ H\left(t_0 - \frac{\bm{k}\cdot\bm{x}_0(t_0)}{c}\right) - H\left(t_0 - \frac{\bm{k}\cdot\bm{x}_1(t_1)}{c} + \frac{L}{c}\right)\right]
y G W ( t 0 ) ≈ 2 k ⋅ n ^ 1 [ H ( t 0 − c k ⋅ x 0 ( t 0 ) ) − H ( t 0 − c k ⋅ x 1 ( t 1 ) + c L ) ]
x 1 ( t 1 ) = x 0 ( t 0 ) + L n ^ \bm{x}_1(t_1) = \bm{x}_0(t_0) + L\hat{\bm{n}}
x 1 ( t 1 ) = x 0 ( t 0 ) + L n ^
y G W ( t 1 ) ≈ 1 2 k ⋅ n ^ [ H ( t 1 − L c − k ⋅ x 0 ( t 0 ) c ) − H ( t 1 − k ⋅ x 1 ( t 1 ) c ) ] y^{\rm GW}(t_1) \approx \frac{1}{2\bm{k}\cdot\hat{\bm{n}}}\left[ H\left(t_1 - \frac{L}{c} - \frac{\bm{k}\cdot\bm{x}_0(t_0)}{c}\right) - H\left(t_1 - \frac{\bm{k}\cdot\bm{x}_1(t_1)}{c}\right)\right]
y G W ( t 1 ) ≈ 2 k ⋅ n ^ 1 [ H ( t 1 − c L − c k ⋅ x 0 ( t 0 ) ) − H ( t 1 − c k ⋅ x 1 ( t 1 ) ) ]
只考虑引力波的效应，接收端与发射端的频率相对偏移量为：
ν ( t ) − ν e m i t ( t − L / c ) ν e m i t ( t − L / c ) = 1 2 [ h ( t ) − h ( t − L / c ) ] \frac{\nu(t)-\nu_{\rm emit}(t-L/c)}{\nu_{\rm emit}(t-L/c)} = \frac{1}{2} \Big[h(t)-h(t-L/c)\Big]
ν e m i t ( t − L / c ) ν ( t ) − ν e m i t ( t − L / c ) = 2 1 [ h ( t ) − h ( t − L / c ) ]
激光不稳定性10KHz量级、预稳频后在30Hz量级
数据噪声
ν ( t ) − ν ( t − L / c ) ν 0 ≈ 1 2 [ h ( t ) − h ( t − L / c ) ] \boxed{\frac{\nu(t)-\nu(t-L/c)}{\nu_0} \approx \frac{1}{2} \Big[h(t) - h(t - L/c)\Big]}
ν 0 ν ( t ) − ν ( t − L / c ) ≈ 2 1 [ h ( t ) − h ( t − L / c ) ]
由于激光波本身的频率不稳定性，这里发射端频率不再稳定为ν 0 \nu_0 ν 0 t − L / c t-L/c t − L / c ν \nu ν ν n \nu_n ν n
ν ( t ) − ν ( t − L / c ) ν 0 − ν n ( t ) − ν n ( t − L / c ) ν 0 ≈ 1 2 [ h ( t ) − h ( t − L / c ) ] \frac{\nu(t)-\nu(t-L/c)}{\nu_0} - \frac{\nu_n(t)-\nu_n(t-L/c)}{\nu_0} \approx \frac{1}{2} \Big[h(t) - h(t - L/c)\Big]
ν 0 ν ( t ) − ν ( t − L / c ) − ν 0 ν n ( t ) − ν n ( t − L / c ) ≈ 2 1 [ h ( t ) − h ( t − L / c ) ]
加速度噪声a = F T M m − ω s 2 X T M a = \frac{F_{\rm TM}}{m} - \omega_s^2X_{\rm TM} a = m F T M − ω s 2 X T M
ν ˙ ( t ) − ν ˙ ( t − L / c ) ν 0 ≈ 1 2 [ h ˙ ( t ) − h ˙ ( t − L / c ) ] + 1 ν 0 [ ν ˙ n ( t ) − ν ˙ n ( t − L / c ) ] + 1 c [ a ( t ) − a ( t − L / c ) ] \begin{aligned} \frac{\dot{\nu}(t)-\dot{\nu}(t-L/c)}{\nu_0} \approx ~ & \frac{1}{2} \Big[\dot{h}(t) - \dot{h}(t - L/c)\Big] + \frac{1}{\nu_0}\Big[\dot{\nu}_n(t)-\dot{\nu}_n(t-L/c)\Big] \\
~&~ + \frac{1}{c}\Big[a(t) - a(t-L/c)\Big]
\end{aligned} ν 0 ν ˙ ( t ) − ν ˙ ( t − L / c ) ≈ 2 1 [ h ˙ ( t ) − h ˙ ( t − L / c ) ] + ν 0 1 [ ν ˙ n ( t ) − ν ˙ n ( t − L / c ) ] + c 1 [ a ( t ) − a ( t − L / c ) ]
散粒噪声是光电感应测量时引入的？5 p m / H z 5\rm pm/\sqrt{Hz} 5 p m / H z 1 0 − 4 / H z 10^{-4}/\rm \sqrt{Hz} 1 0 − 4 / H z 2 p m / H z 2\rm pm/\sqrt{Hz} 2 p m / H z 1 0 − 21 / H z 10^{-21}/\rm \sqrt{Hz} 1 0 − 2 1 / H z 1 0 − 13 / H z 10^{-13}/\rm \sqrt{Hz} 1 0 − 1 3 / H z 1 p m / H z 1\rm pm/\sqrt{Hz} 1 p m / H z 1 0 − 13 s / H z 10^{-13}\rm s/\sqrt{Hz} 1 0 − 1 3 s / H z 1 p m / H z 1\rm pm/\sqrt{Hz} 1 p m / H z
1pm的要求是什么意思？？8 p m / H z 8\rm pm/\sqrt{Hz} 8 p m / H z 3 × 1 0 − 15 m s − 2 / H z 3\times10^{-15}\rm ms^{-2}/\sqrt{Hz} 3 × 1 0 − 1 5 m s − 2 / H z
卫星轨道分析
卫星编队的轨道分析通常使用CW参考系，即卫星编队的共动参考系：取参考点绕中心天体做圆轨道 运动，以参考点为原点，坐标轴分别沿轨道径向、切向和法向，随参考点一起运动(非惯性系)。CW参考系由Clohessy & Wiltshire提出，由于卫星偏离参考点通常远小于其轨道半径，因此可在参考点附近做小量展开分析卫星运动。
在CW参考系下，满足轨道稳定性，同时与原点(参考点)距离恒定的粒子运动轨迹为与x y xy x y ± 6 0 ∘ \pm 60^{\circ} ± 6 0 ∘ 2 π 3 \frac{2\pi}{3} 3 2 π
当然，上述CW参考系下的讨论相当于到偏心率一阶的近似，实际上卫星构型并不像上面所说的完全稳定，三颗卫星间距离存在一定波动，而根据Nayak et al. 2006的分析，当卫星平面倾斜角取π 3 + 5 8 ι \frac{\pi}{3} + \frac{5}{8}\iota 3 π + 8 5 ι ι \iota ι
轨道运动描述
取参考点在黄道面内做圆轨道运动，半径为日地平均距离R ∼ 1 A U ∼ 1.5 × 1 0 8 k m R \sim 1AU \sim 1.5\times 10^8\rm km R ∼ 1 A U ∼ 1 . 5 × 1 0 8 k m L ∼ 2.5 × 1 0 6 k m L\sim 2.5\times 10^6 \rm km L ∼ 2 . 5 × 1 0 6 k m ϵ \epsilon ϵ R = 1 A U R=1\rm AU R = 1 A U ∼ 1 0 − 6 \sim 10^{-6} ∼ 1 0 − 6 R R R
如上图所示，取轨道远心点为对应轨道最高点，利用简单几何关系，卫星相对黄道面高度为L 3 sin ϵ \frac{L}{\sqrt{3}}\sin\epsilon 3 L sin ϵ R + L 3 sin ϵ R+\frac{L}{\sqrt{3}}\sin\epsilon R + 3 L sin ϵ
tan ε = L 3 sin ϵ / ( R + L 3 cos ϵ ) , R ( 1 + e ) = ( L 3 sin ϵ ) 2 + ( R + L 3 cos ϵ ) 2 \textstyle \tan\varepsilon = \frac{L}{\sqrt{3}}\sin\epsilon \Big /(R+\frac{L}{\sqrt{3}}\cos\epsilon), ~ R(1+e) = \sqrt{\left(\frac{L}{\sqrt{3}}\sin\epsilon\right)^2 + \left(R+\frac{L}{\sqrt{3}}\cos\epsilon\right)^2}
tan ε = 3 L sin ϵ / ( R + 3 L cos ϵ ) , R ( 1 + e ) = ( 3 L sin ϵ ) 2 + ( R + 3 L cos ϵ ) 2
由此卫星轨道倾角和偏心率为：
ε = arctan ( 2 3 ι sin ϵ 1 + 2 3 ι cos ϵ ) e = 1 + 4 3 ι cos ϵ + 4 3 ι 2 − 1 \begin{aligned}
\varepsilon &= \arctan\left(\frac{\frac{2}{\sqrt{3}}\iota\sin\epsilon}{1 + \frac{2}{\sqrt{3}}\iota\cos\epsilon}\right)\\
e &= \sqrt{1 + \frac{4}{\sqrt{3}}\iota \cos\epsilon + \frac{4}{3}\iota^2} - 1
\end{aligned} ε e = arctan ( 1 + 3 2 ι cos ϵ 3 2 ι sin ϵ ) = 1 + 3 4 ι cos ϵ + 3 4 ι 2 − 1
其中ι = L 2 R ∼ 0.0083 \iota=\frac{L}{2R} \sim 0.0083 ι = 2 R L ∼ 0 . 0 0 8 3 ϵ = π 3 \epsilon=\frac{\pi}{3} ϵ = 3 π
ε = arctan ( ι 1 + ι / 3 ) e = 1 + 2 3 ι + 4 3 ι 2 − 1 \boxed{\begin{aligned}
\varepsilon &= \arctan\left(\frac{\iota}{1 + \iota/\sqrt{3}}\right)\\
e &= \sqrt{1 + \frac{2}{\sqrt{3}}\iota + \frac{4}{3}\iota^2} - 1
\end{aligned}} ε e = arctan ( 1 + ι / 3 ι ) = 1 + 3 2 ι + 3 4 ι 2 − 1
对小量ι \iota ι
ε ∼ ι ∼ 3 e \varepsilon \sim \iota \sim \sqrt{3}e
ε ∼ ι ∼ 3 e
显然臂长L L L
LISA轨道偏心率e ∼ 0.0096 e \sim 0.0096 e ∼ 0 . 0 0 9 6 ε ∼ 0.9 6 ∘ \varepsilon \sim 0.96^\circ ε ∼ 0 . 9 6 ∘ Colpi et al. 2024 )。∼ 0.0167 \sim 0.0167 ∼ 0 . 0 1 6 7 − 6 0 ∘ -60^\circ − 6 0 ∘
前面的分析限制了轨道形状R , e R, e R , e ε \varepsilon ε π 2 \frac{\pi}{2} 2 π π 2 \frac{\pi}{2} 2 π y y y − ε -\varepsilon − ε
x = R ( cos ψ − e ) y = R 1 − e 2 sin ψ \begin{aligned}
x &= R(\cos\psi - e)\\
y &= R\sqrt{1-e^2}\sin\psi
\end{aligned} x y = R ( cos ψ − e ) = R 1 − e 2 sin ψ
其中ψ \psi ψ y y y − ε -\varepsilon − ε
x = R ( cos ψ − e ) cos ε y = R 1 − e 2 sin ψ z = − R ( cos ψ − e ) sin ε \begin{aligned}
x &= R(\cos\psi - e)\cos\varepsilon\\
y &= R\sqrt{1-e^2}\sin\psi\\
z &= -R(\cos\psi - e)\sin\varepsilon\\
\end{aligned} x y z = R ( cos ψ − e ) cos ε = R 1 − e 2 sin ψ = − R ( cos ψ − e ) sin ε
为获得坐标随时间的演化，要建立偏近点角ψ \psi ψ
ψ ( t ) − e sin ψ ( t ) = ω ˉ ( t − t 0 ) + m 0 \psi(t) - e\sin\psi(t) = \bar{\omega} (t-t_0) + m_0
ψ ( t ) − e sin ψ ( t ) = ω ˉ ( t − t 0 ) + m 0
方程右侧为平近点角m ( t ) m(t) m ( t ) ω ˉ \bar{\omega} ω ˉ 2 π 1 y r \frac{2\pi}{1\rm yr} 1 y r 2 π m 0 m_0 m 0 t 0 t_0 t 0
最后，卫星实际轨道可由上述基准轨道绕z z z 2 π 3 \frac{2\pi}{3} 3 2 π 2 π 3 \frac{2\pi}{3} 3 2 π
( x k y k z k ) = ( cos λ k − sin λ k 0 sin λ k cos λ k 0 0 0 1 ) ( R ( cos ψ k − e ) cos ε R 1 − e 2 sin ψ k − R ( cos ψ k − e ) sin ε ) λ k = λ 0 + 2 π 3 ( k − 1 ) , k = 1 , 2 , 3 ψ k − e sin ψ k = ω ˉ ( t − t 0 ) + m 0 − 2 π 3 ( k − 1 ) \boxed{\begin{aligned}
\begin{pmatrix}
x_k\\
y_k\\
z_k
\end{pmatrix}
&= \begin{pmatrix}
\cos\lambda_k & -\sin\lambda_k & 0\\
\sin\lambda_k & \cos\lambda_k & 0\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
R(\cos\psi_k - e)\cos\varepsilon\\
R\sqrt{1-e^2}\sin\psi_k\\
-R(\cos\psi_k - e)\sin\varepsilon\\
\end{pmatrix}\\
\lambda_k &= \lambda_0 + \frac{2\pi}{3}(k-1), ~~~~ k = 1,2,3 \\
\psi_k &- e\sin\psi_k = \bar{\omega}(t-t_0) + m_0 - \frac{2\pi}{3}(k-1)
\end{aligned}} ⎝ ⎛ x k y k z k ⎠ ⎞ λ k ψ k = ⎝ ⎛ cos λ k sin λ k 0 − sin λ k cos λ k 0 0 0 1 ⎠ ⎞ ⎝ ⎛ R ( cos ψ k − e ) cos ε R 1 − e 2 sin ψ k − R ( cos ψ k − e ) sin ε ⎠ ⎞ = λ 0 + 3 2 π ( k − 1 ) , k = 1 , 2 , 3 − e sin ψ k = ω ˉ ( t − t 0 ) + m 0 − 3 2 π ( k − 1 )
其中λ 0 \lambda_0 λ 0 m 0 m_0 m 0 t 0 t_0 t 0
这里轨道形式上与Cornish & Rubbo 2003/Rubbo et al. 2004附录的公式不同，但两者等价。这里是从偏近点角出发推导，而相关文章是从真近点角出发推导。具体的，在轨道平面内由开普勒半径r r r γ \gamma γ y y y z z z 3 e \sqrt{3}e 3 e
x = r cos γ y = r sin γ R y ( ε ) → x = r cos γ cos ε y = r sin γ z = − r cos γ sin ε R z ( β ) → \begin{matrix}
x = r\cos\gamma\\
y = r\sin\gamma
\end{matrix}
~ ~ ~ \underrightarrow{\mathcal{R}_y(\varepsilon)} ~ ~ ~
\begin{matrix}
x = r\cos\gamma \cos\varepsilon~~\\
y = r\sin\gamma~~~~~~~~~~\\
z = -r\cos\gamma \sin\varepsilon
\end{matrix}
~ ~ ~ \underrightarrow{\mathcal{R}_z(\beta)} x = r cos γ y = r sin γ R y ( ε ) x = r cos γ cos ε y = r sin γ z = − r cos γ sin ε R z ( β )
这里开普勒半径r = R ( 1 − e 2 ) 1 + e cos γ r=\frac{R(1-e^2)}{1+e\cos\gamma} r = 1 + e c o s γ R ( 1 − e 2 ) γ \gamma γ β \beta β λ k \lambda_k λ k λ \lambda λ λ 0 \lambda_0 λ 0 α − β \alpha-\beta α − β κ \kappa κ m 0 + λ 0 m_0 + \lambda_0 m 0 + λ 0
关于参考系
计时通常采用太阳质心坐标时TCB，英文Barycentric Coordinate Time，缩写TCB来自法语Temps-coordonnée barycentrique。TCB属于质心天球参考系BCRS定义的一部分，但黄道坐标系也可以用。
轨道近似及臂长变化
x = R ( cos ψ − e ) cos ε y = R 1 − e 2 sin ψ z = − R ( cos ψ − e ) sin ε \begin{aligned}
x &= R(\cos\psi - e)\cos\varepsilon\\
y &= R\sqrt{1-e^2}\sin\psi\\
z &= -R(\cos\psi - e)\sin\varepsilon\\
\end{aligned} x y z = R ( cos ψ − e ) cos ε = R 1 − e 2 sin ψ = − R ( cos ψ − e ) sin ε
这里对上述基准轨道进行近似，轨道倾角和偏心率都展开到ι \iota ι ε = 3 e \varepsilon=\sqrt{3}e ε = 3 e ψ \psi ψ
ψ ( t ) − e sin ψ ( t ) = m ( t ) \psi(t) - e\sin\psi(t) = m(t)
ψ ( t ) − e sin ψ ( t ) = m ( t )
考虑到偏心率e e e
ψ 0 = m , ψ 1 = m + e sin ψ 0 , ψ 2 = m + e sin ψ 1 , . . . \psi_0 = m, ~~~ \psi_1 = m + e \sin \psi_0, ~~~ \psi_2 = m + e \sin \psi_1, ...
ψ 0 = m , ψ 1 = m + e sin ψ 0 , ψ 2 = m + e sin ψ 1 , . . .
到偏心率的二阶有：
ψ ≈ ψ 2 = m + e sin [ m + e sin ( m ) ] = m + e sin ( m ) cos [ e sin ( m ) ] + e cos ( m ) sin [ e sin ( m ) ] ≈ m + e sin ( m ) + e 2 cos ( m ) sin ( m ) \begin{aligned}
\psi &\approx \psi_2 = m + e \sin [m + e \sin (m)]\\
&= m + e \sin (m) \cos[e \sin (m)] + e \cos (m) \sin[e \sin (m)]\\
&\approx m + e \sin (m) + e^2 \cos (m)\sin (m)\\
\end{aligned} ψ ≈ ψ 2 = m + e sin [ m + e sin ( m ) ] = m + e sin ( m ) cos [ e sin ( m ) ] + e cos ( m ) sin [ e sin ( m ) ] ≈ m + e sin ( m ) + e 2 cos ( m ) sin ( m )
由此，轨道方程中所有项都可展开到偏心率二阶：
sin ψ ≈ sin ( m ) + e sin ( m ) cos ( m ) + e 2 sin ( m ) [ cos 2 ( m ) − 1 2 sin 2 ( m ) ] cos ψ ≈ cos ( m ) − e sin 2 ( m ) − 3 2 e 2 cos ( m ) sin 2 ( m ) cos ε ≈ 1 − 1 2 ε 2 ≈ 1 − 3 2 e 2 sin ε ≈ ε ≈ 3 e 1 − e 2 ≈ 1 − 1 2 e 2 \begin{aligned}
\sin\psi &\approx \sin (m) + e \sin(m)\cos(m) + e^2 \sin(m)[\cos^2 (m) - \frac{1}{2}\sin^2 (m)]\\
\cos\psi &\approx \cos (m) - e \sin^2 (m) - \frac{3}{2}e^2 \cos(m)\sin^2 (m)\\
\cos\varepsilon &\approx 1 - \frac{1}{2}\varepsilon^2 \approx 1 - \frac{3}{2}e^2\\
\sin\varepsilon &\approx \varepsilon \approx \sqrt{3}e\\
\sqrt{1-e^2} &\approx 1-\frac{1}{2}e^2
\end{aligned} sin ψ cos ψ cos ε sin ε 1 − e 2 ≈ sin ( m ) + e sin ( m ) cos ( m ) + e 2 sin ( m ) [ cos 2 ( m ) − 2 1 sin 2 ( m ) ] ≈ cos ( m ) − e sin 2 ( m ) − 2 3 e 2 cos ( m ) sin 2 ( m ) ≈ 1 − 2 1 ε 2 ≈ 1 − 2 3 e 2 ≈ ε ≈ 3 e ≈ 1 − 2 1 e 2
带入轨道方程，保留到偏心率二阶项有：
x = R cos ( m ) − 1 2 R e [ 3 − cos ( 2 m ) ] + 1 8 R e 2 [ 3 cos ( 3 m ) − 10 cos ( m ) − 5 cos ( m ) ] y = R sin ( m ) + 1 2 R e sin ( 2 m ) + 1 8 R e 2 [ 3 sin ( 3 m ) − 10 sin ( m ) + 5 sin ( m ) ] z = − 3 R e cos ( m ) + 3 R e 2 [ sin 2 ( m ) + 1 ] \small\begin{aligned}
x &= R\cos (m) - \frac{1}{2}Re [3- \cos(2m)] + \frac{1}{8}Re^2 [3\cos(3m) -10\cos(m) - 5\cos(m) ]\\
y &= R\sin (m) + \frac{1}{2}Re \sin(2m) + \frac{1}{8}Re^2 [3\sin(3m) - 10\sin(m) + 5\sin(m)]\\
z &= -\sqrt{3} R e \cos(m) + \sqrt{3} R e^2 [\sin^2(m) + 1]\\
\end{aligned} x y z = R cos ( m ) − 2 1 R e [ 3 − cos ( 2 m ) ] + 8 1 R e 2 [ 3 cos ( 3 m ) − 1 0 cos ( m ) − 5 cos ( m ) ] = R sin ( m ) + 2 1 R e sin ( 2 m ) + 8 1 R e 2 [ 3 sin ( 3 m ) − 1 0 sin ( m ) + 5 sin ( m ) ] = − 3 R e cos ( m ) + 3 R e 2 [ sin 2 ( m ) + 1 ]
考虑到m m m α − β \alpha-\beta α − β z z z β \beta β
近似到偏心1一阶，参考点轨道为黄道面内圆轨道，卫星臂长恒定为2 3 R e 2\sqrt{3}Re 2 3 R e 3 3 2 R e 2 ∼ 3 8 L 2 R \frac{3\sqrt{3}}{2}Re^2\sim\frac{\sqrt{3}}{8}\frac{L^2}{R} 2 3 3 R e 2 ∼ 8 3 R L 2
探测响应调制
运动导致干涉臂指向(及臂长)变化会影响探测响应。对于地基观测，恒星级双黑洞观测时标t ∼ 10 s t\sim 10s t ∼ 1 0 s
投影部分，
臂长变化
L 12 ( t ) = L { 1 + e 32 [ 15 sin ( α − λ + π 6 ) − cos ( 3 α − 3 λ ) ] } L 13 ( t ) = L { 1 + e 32 [ − 15 sin ( α − λ − π 6 ) − cos ( 3 α − 3 λ ) ] } L 23 ( t ) = L { 1 − e 32 [ 15 cos ( α − λ ) − cos ( 3 α − 3 λ ) ] } \begin{aligned}
L_{12}(t) &= L\left\{ 1 + \frac{e}{32}\left[15\sin(\alpha-\lambda+\frac{\pi}{6}) - \cos(3\alpha-3\lambda)\right] \right\}\\
L_{13}(t) &= L\left\{ 1 + \frac{e}{32}\left[-15\sin(\alpha-\lambda-\frac{\pi}{6}) - \cos(3\alpha-3\lambda)\right] \right\}\\
L_{23}(t) &= L\left\{ 1 - \frac{e}{32}\Big[15\cos(\alpha-\lambda) - \cos(3\alpha-3\lambda) \Big] \right\}
\end{aligned} L 1 2 ( t ) L 1 3 ( t ) L 2 3 ( t ) = L { 1 + 3 2 e [ 1 5 sin ( α − λ + 6 π ) − cos ( 3 α − 3 λ ) ] } = L { 1 + 3 2 e [ − 1 5 sin ( α − λ − 6 π ) − cos ( 3 α − 3 λ ) ] } = L { 1 − 3 2 e [ 1 5 cos ( α − λ ) − cos ( 3 α − 3 λ ) ] }
L 12 ( t ) = L { 1 + e 32 [ 15 sin ( m + π 6 ) − cos ( 3 m ) ] } L 13 ( t ) = L { 1 + e 32 [ − 15 sin ( m − π 6 ) − cos ( 3 m ) ] } L 23 ( t ) = L { 1 − e 32 [ 15 cos ( m ) − cos ( 3 m ) ] } m ( t ) = ω ˉ ( t − t 0 ) + m 0 \begin{aligned}
L_{12}(t) &= L\left\{ 1 + \frac{e}{32}\left[15\sin(m +\frac{\pi}{6}) - \cos(3m)\right] \right\}\\
L_{13}(t) &= L\left\{ 1 + \frac{e}{32}\left[-15\sin(m -\frac{\pi}{6}) - \cos(3m)\right] \right\}\\
L_{23}(t) &= L\left\{ 1 - \frac{e}{32}\Big[15\cos(m) - \cos(3m) \Big] \right\}\\
m(t) &= \bar{\omega}(t-t_0) + m_0
\end{aligned} L 1 2 ( t ) L 1 3 ( t ) L 2 3 ( t ) m ( t ) = L { 1 + 3 2 e [ 1 5 sin ( m + 6 π ) − cos ( 3 m ) ] } = L { 1 + 3 2 e [ − 1 5 sin ( m − 6 π ) − cos ( 3 m ) ] } = L { 1 − 3 2 e [ 1 5 cos ( m ) − cos ( 3 m ) ] } = ω ˉ ( t − t 0 ) + m 0
探测响应
D P ( t ) = ( x ^ 12 a x ^ 12 b − x ^ 13 a x ^ 13 b ) e a b P \begin{aligned}
D^P(t) = \left(\hat{x}^a_{12}\hat{x}^b_{12} - \hat{x}^a_{13}\hat{x}^b_{13}\right)e^P_{ab}
\end{aligned} D P ( t ) = ( x ^ 1 2 a x ^ 1 2 b − x ^ 1 3 a x ^ 1 3 b ) e a b P
sin Υ ← 3 2 , Υ ς \sin\Upsilon \leftarrow \frac{\sqrt{3}}{2}, \Upsilon\varsigma sin Υ ← 2 3 , Υ ς
D + ( t ) = sin Υ 32 { − 36 sin 2 θ sin ( 2 α − 2 λ ) + ( 3 + cos 2 θ ) × [ cos 2 φ ( 9 sin 2 λ − sin ( 4 α − 2 λ ) ) + sin 2 φ ( cos ( 4 α − 2 λ ) − 9 cos 2 λ ) ] − 4 3 sin 2 θ [ sin ( 3 α − 2 λ − φ ) − 3 sin ( α − 2 λ + φ ) ] } D × ( t ) = sin Υ 8 { cos θ [ 9 cos ( 2 λ − 2 φ ) − cos ( 4 α − 2 λ − 2 φ ) ] − 2 3 sin θ [ cos ( 3 α − 2 λ − φ ) + 3 cos ( α − 2 λ + φ ) ] } \begin{aligned}
\small D^+(t) = \frac{\sin\Upsilon}{32} \bigg\{& \small -36\sin^2\theta ~ \sin(2\alpha -2\lambda) + (3+\cos2\theta) \times \\
&\small \Big[ \cos2\varphi \Big(9\sin2\lambda - \sin(4\alpha-2\lambda) \Big) + \sin2\varphi \Big(\cos(4\alpha -2\lambda) - 9 \cos2\lambda\Big)\Big]\\
&\small - 4\sqrt{3} \sin2\theta\Big[\sin(3\alpha -2\lambda-\varphi) - 3\sin(\alpha - 2\lambda + \varphi)\Big] \bigg\} \\
\small D^\times(t) = \frac{\sin\Upsilon}{8} \bigg\{ & \small \cos\theta ~ \Big[9\cos(2\lambda-2\varphi) - \cos(4\alpha-2\lambda-2\varphi)\Big]\\
&\small - 2\sqrt{3}\sin\theta ~ \Big[\cos(3\alpha - 2\lambda-\varphi) + 3\cos(\alpha -2\lambda + \varphi)\Big]\bigg\}
\end{aligned} D + ( t ) = 3 2 sin Υ { D × ( t ) = 8 sin Υ { − 3 6 sin 2 θ sin ( 2 α − 2 λ ) + ( 3 + cos 2 θ ) × [ cos 2 φ ( 9 sin 2 λ − sin ( 4 α − 2 λ ) ) + sin 2 φ ( cos ( 4 α − 2 λ ) − 9 cos 2 λ ) ] − 4 3 sin 2 θ [ sin ( 3 α − 2 λ − φ ) − 3 sin ( α − 2 λ + φ ) ] } cos θ [ 9 cos ( 2 λ − 2 φ ) − cos ( 4 α − 2 λ − 2 φ ) ] − 2 3 sin θ [ cos ( 3 α − 2 λ − φ ) + 3 cos ( α − 2 λ + φ ) ] }
D + ( t ) = 3 64 { − 36 sin 2 θ sin ( 2 α − 2 λ ) + ( 3 + cos 2 θ ) × [ cos 2 φ ( 9 sin 2 λ − sin ( 4 α − 2 λ ) ) + sin 2 φ ( cos ( 4 α − 2 λ ) − 9 cos 2 λ ) ] − 4 3 sin 2 θ [ sin ( 3 α − 2 λ − φ ) − 3 sin ( α − 2 λ + φ ) ] } D × ( t ) = 1 16 { 3 cos θ [ 9 cos ( 2 λ − 2 φ ) − cos ( 4 α − 2 λ − 2 φ ) ] − 6 sin θ [ cos ( 3 α − 2 λ − φ ) + 3 cos ( α − 2 λ + φ ) ] } \begin{aligned}
\small D^+(t) = \frac{\sqrt{3}}{64} \bigg\{& \small -36\sin^2\theta ~ \sin(2\alpha -2\lambda) + (3+\cos2\theta) \times \\
&\small \Big[ \cos2\varphi \Big(9\sin2\lambda - \sin(4\alpha-2\lambda) \Big) + \sin2\varphi \Big(\cos(4\alpha -2\lambda) - 9 \cos2\lambda\Big)\Big]\\
&\small - 4\sqrt{3} \sin2\theta\Big[\sin(3\alpha -2\lambda-\varphi) - 3\sin(\alpha - 2\lambda + \varphi)\Big] \bigg\} \\
\small D^\times(t) = \frac{1}{16} \bigg\{ & \small \sqrt{3}\cos\theta ~ \Big[9\cos(2\lambda-2\varphi) - \cos(4\alpha-2\lambda-2\varphi)\Big]\\
&\small - 6\sin\theta ~ \Big[\cos(3\alpha - 2\lambda-\varphi) + 3\cos(\alpha -2\lambda + \varphi)\Big]\bigg\}
\end{aligned} D + ( t ) = 6 4 3 { D × ( t ) = 1 6 1 { − 3 6 sin 2 θ sin ( 2 α − 2 λ ) + ( 3 + cos 2 θ ) × [ cos 2 φ ( 9 sin 2 λ − sin ( 4 α − 2 λ ) ) + sin 2 φ ( cos ( 4 α − 2 λ ) − 9 cos 2 λ ) ] − 4 3 sin 2 θ [ sin ( 3 α − 2 λ − φ ) − 3 sin ( α − 2 λ + φ ) ] } 3 cos θ [ 9 cos ( 2 λ − 2 φ ) − cos ( 4 α − 2 λ − 2 φ ) ] − 6 sin θ [ cos ( 3 α − 2 λ − φ ) + 3 cos ( α − 2 λ + φ ) ] }
其中 α = 2 π f m t + κ \alpha=2 \pi f_m t + \kappa α = 2 π f m t + κ θ , ϕ \theta, \phi θ , ϕ κ , λ \kappa, \lambda κ , λ
\begin{aligned}
\end{aligned}
坐标变换
考虑到探测器轨道运动，在黄道参考系对系统进行描述更为方便。前面推导的系统转移函数为矢量(张量)形式，不依赖具体参考系。因此形式上，转移函数保持不变，只是此时x ^ , y ^ \hat{x}, \hat{y} x ^ , y ^
虽然转移函数形式上保持不变，张量缩并、矢量点乘结果也都与坐标系选择无关，但实际计算时要将上述表达式展开为具体的方位角表示，是依赖坐标选择的，需要在不同坐标系的角度之间进行转换。
θ S , ψ S , θ L , ψ L \theta_S, \psi_S, \theta_L, \psi_L
θ S , ψ S , θ L , ψ L
波源的方位、波源轨道角动量
利用黄道坐标系(太阳系质心SSB参考系)建立引力波源与探测器的关系。
λ , β \lambda, \beta
λ , β
经度、维度
信号调制
h d e t ( t ) = h S S B ( t − k ^ ⋅ r ⃗ d e t c ) = h S S B ( t ) e − i ω k ^ ⋅ r ⃗ d e t c \bm{h}_{\rm det}(t) = \bm{h}_{\rm \tiny SSB}\left(t - \hat{k}\cdot\frac{\vec{r}_{\rm det}}{c}\right) = \bm{h}_{\rm \tiny SSB}(t) e^{- i\omega\hat{k}\cdot\frac{\vec{r}_{\rm det}}{c}}
h d e t ( t ) = h S S B ( t − k ^ ⋅ c r d e t ) = h S S B ( t ) e − i ω k ^ ⋅ c r d e t
注意，虽然考虑到探测器运动，x ^ \hat{x} x ^ r ⃗ d e t \vec{r}_{\rm det} r d e t r ⃗ d e t \vec{r}_{\rm det} r d e t x ^ \hat{x} x ^
1 2 x ^ i ( t − L c ) x ^ j ( t − L c ) e i j P e − i ω [ 1 + k ^ ⋅ x ^ ( t − L c ) ] L 2 c s i n c { ω [ 1 + k ^ ⋅ x ^ ( t − L c ) ] L 2 c } e − i ω k ^ ⋅ r ⃗ 2 ( t − L c ) − L x ^ ( t − L c ) c + 1 2 x ^ i ( t − 2 L c ) x ^ j ( t − 2 L c ) e i j P e − i ω [ 3 + k ^ ⋅ x ^ ( t − 2 L c ) ] L 2 c s i n c { ω [ 1 − k ^ ⋅ x ^ ( t − L 2 c ) ] L c } e − i ω k ^ ⋅ r ⃗ 1 ( t − 2 L c ) c \begin{aligned}
&\small \frac{1}{2}\hat{x}^i(t-{\textstyle \frac{L}{c}}) \hat{x}^j(t-{\textstyle \frac{L}{c}}) e_{ij}^P e^{-i\omega [1 + \hat{k}\cdot\hat{x}(t-\frac{L}{c})]\frac{L}{2c}} ~ {\rm sinc}\left\{\omega [1 + \hat{k}\cdot\hat{x}(t-{\textstyle \frac{L}{c}})] {\textstyle \frac{L}{2c}}\right\} e^{-i\omega \hat{k} \cdot \frac{\vec{r}_2(t-\frac{L}{c}) - L\hat{x}(t-\frac{L}{c})}{c}}\\
&\small + \frac{1}{2}\hat{x}^i(t-{\textstyle \frac{2L}{c}}) \hat{x}^j(t-{\textstyle \frac{2L}{c}}) e_{ij}^P e^{-i\omega [3+\hat{k} \cdot \hat{x}(t-\frac{2L}{c})] \frac{L}{2c}} ~ {\rm sinc}\left\{\omega [1 - \hat{k}\cdot\hat{x}(t-{\textstyle \frac{L}{2c}})] {\textstyle \frac{L}{c}}\right\} e^{-i\omega \hat{k} \cdot \frac{\vec{r}_1(t-\frac{2L}{c})}{c}}
\end{aligned} 2 1 x ^ i ( t − c L ) x ^ j ( t − c L ) e i j P e − i ω [ 1 + k ^ ⋅ x ^ ( t − c L ) ] 2 c L s i n c { ω [ 1 + k ^ ⋅ x ^ ( t − c L ) ] 2 c L } e − i ω k ^ ⋅ c r 2 ( t − c L ) − L x ^ ( t − c L ) + 2 1 x ^ i ( t − c 2 L ) x ^ j ( t − c 2 L ) e i j P e − i ω [ 3 + k ^ ⋅ x ^ ( t − c 2 L ) ] 2 c L s i n c { ω [ 1 − k ^ ⋅ x ^ ( t − 2 c L ) ] c L } e − i ω k ^ ⋅ c r 1 ( t − c 2 L )
由于卫星运动，激光指向其实要有一定提前量
x ^ i j ( t i ) ≡ r ⃗ j ( t j ) − r ⃗ i ( t i ) ℓ i j ( t i ) ℓ i j ( t i ) ≡ ∥ r ⃗ j ( t j ) − r ⃗ i ( t i ) ∥ = ∥ r ⃗ j [ t i + ℓ i j ( t i ) c ] − r ⃗ i ( t i ) ∥ L i j ( t i ) ≡ ∥ r ⃗ j ( t i ) − r ⃗ i ( t i ) ∥ \begin{aligned}
\hat{x}_{ij}(t_i) &\equiv \frac{\vec{r}_j(t_j) - \vec{r}_i(t_i)}{\ell_{ij}(t_i)}\\
\ell_{ij}(t_i) &\equiv \|\vec{r}_j(t_j) - \vec{r}_i(t_i)\| = \left\|\vec{r}_j\left[t_i + {\textstyle \frac{\ell_{ij}(t_i)}{c}}\right] - \vec{r}_i(t_i)\right\|\\
L_{ij}(t_i) &\equiv \|\vec{r}_j(t_i) - \vec{r}_i(t_i)\|
\end{aligned} x ^ i j ( t i ) ℓ i j ( t i ) L i j ( t i ) ≡ ℓ i j ( t i ) r j ( t j ) − r i ( t i ) ≡ ∥ r j ( t j ) − r i ( t i ) ∥ = ∥ ∥ ∥ ∥ r j [ t i + c ℓ i j ( t i ) ] − r i ( t i ) ∥ ∥ ∥ ∥ ≡ ∥ r j ( t i ) − r i ( t i ) ∥
这里 ℓ i j \ell_{ij} ℓ i j L i j L_{ij} L i j ℓ i j , r ⃗ j \ell_{ij}, \vec{r}_j ℓ i j , r j v c \frac{v}{c} c v
r ⃗ j [ t i + ℓ i j ( t i ) c ] = r ⃗ j ( t i ) + ∫ t i t i + ℓ i j ( t i ) c v ⃗ j ( τ ) d τ ≈ r ⃗ j ( t i ) + ℓ i j ( t i ) c v ⃗ j ( t i ) \vec{r}_j\left[t_i + {\textstyle \frac{\ell_{ij}(t_i)}{c}}\right] = \vec{r}_j(t_i) + \int_{t_i}^{t_i + \frac{\ell_{ij}(t_i)}{c}} \vec{v}_j(\tau) d\tau \approx \vec{r}_j(t_i) + {\textstyle \frac{\ell_{ij}(t_i)}{c}} \vec{v}_j(t_i)
r j [ t i + c ℓ i j ( t i ) ] = r j ( t i ) + ∫ t i t i + c ℓ i j ( t i ) v j ( τ ) d τ ≈ r j ( t i ) + c ℓ i j ( t i ) v j ( t i )
ℓ i j ( t i ) = ∥ r ⃗ j ( t i ) − r ⃗ i ( t i ) + ℓ i j ( t i ) c v ⃗ j ( t i ) ∥ = \ell_{ij}(t_i) = \left\|\vec{r}_j(t_i) - \vec{r}_i(t_i) + {\textstyle \frac{\ell_{ij}(t_i)}{c}} \vec{v}_j(t_i)\right\| =
ℓ i j ( t i ) = ∥ ∥ ∥ ∥ r j ( t i ) − r i ( t i ) + c ℓ i j ( t i ) v j ( t i ) ∥ ∥ ∥ ∥ =
ℓ i j ( t i ) ≈ L i j 1 + [ v j ( t i ) c ] 2 ≈ L i j { 1 + 1 2 [ v j ( t i ) c ] 2 } \ell_{ij}(t_i) \approx L_{ij} \sqrt{1 + \left[\frac{v_j(t_i)}{c}\right]^2} \approx L_{ij} \left\{1 + \frac{1}{2}\left[\frac{v_j(t_i)}{c}\right]^2\right\}
ℓ i j ( t i ) ≈ L i j 1 + [ c v j ( t i ) ] 2 ≈ L i j { 1 + 2 1 [ c v j ( t i ) ] 2 }
ℓ i j ( t i ) = L i j ( t i ) [ 1 + x ^ i j ( t i ) ⋅ v ⃗ j ( t i ) c + o ( v 2 c ) ] \ell_{ij}(t_i) = L_{ij}(t_i)\left[1 + \hat{x}_{ij}(t_i)\cdot\frac{\vec{v}_j(t_i)}{c} + o\left(\frac{v^2}{c}\right)\right]
ℓ i j ( t i ) = L i j ( t i ) [ 1 + x ^ i j ( t i ) ⋅ c v j ( t i ) + o ( c v 2 ) ]
考虑卫星运动的提前量导致的光程变化在v c ≈ 1 c 2 π f m R ≈ 1 0 − 4 \frac{v}{c} \approx \frac{1}{c}2\pi f_m R \approx 10^-4 c v ≈ c 1 2 π f m R ≈ 1 0 − 4 1 / 100 1/100 1 / 1 0 0 5 × 1 0 9 m 5\times10^9 \rm m 5 × 1 0 9 m 100 k m 100\rm km 1 0 0 k m 1 0 4 k m 10^4\rm km 1 0 4 k m
对于目前的空间探测，激光沿干涉臂传播时间仅约10 10 1 0
F S S B P ( f , t ) = F P ( f , t ) e − i 2 π f k ^ ⋅ r ⃗ d e t ( t ) c \boxed{ F_{\rm \tiny SSB}^P(f, t) = F^P(f, t) e^{- i 2\pi f\hat{k}\cdot\frac{\vec{r}_{\rm det}(t)}{c}} }
F S S B P ( f , t ) = F P ( f , t ) e − i 2 π f k ^ ⋅ c r d e t ( t )
注意，这里的响应调制项是频率依赖的。
刚性绝热近似 Rigid Adiabatic Approximation c f / f ˙ ≪ L c f/\dot{f} \ll L c f / f ˙ ≪ L f < c 2 π L f < \frac{c}{2\pi L} f < 2 π L c
时间延迟干涉
通常讨论TDI是针对外差相位(距离变化)测量的，实际中到底采用相位(距离)，还是频率(速度)或者啁啾度(加速度)还是一个开放问题，这涉及相位计的内部设计和处理流程，包括滤波、量化等过程的影响。在臂长(相等？)不变的情况，不同物理量的TDI可简单实现转换，当考虑到臂长变化不同物理量的TDI需要具体讨论。Bayle et al. 2021中就给除了频率的TDI，Spadaro et al. 2023提出了加速度TDI，但是在不考虑臂长变化的前提下的，可以扩展。
相位、相对频移、
暂时不考虑多普勒效应，对于分光干涉系统
似乎有两种思路：
一种是双臂干涉直接对应X、Y、Z通道TDI的响应
在臂长相等情况下，原则上并不需要TDI，但也可以按TDI进行组合，此时时间延迟算子是同一个，可以等效视为0代TDI
相应TDI组合的噪声曲线？
以激光接收端 为参考，x ^ \hat{x} x ^
s i j ( f , t ) = 1 2 x ^ a x ^ b h ~ a b ( f ) e i ω ( t ∣ r ⃗ i − k ^ ⋅ r ⃗ i c ) 1 i ω ( 1 − k ^ ⋅ x ^ i j ) [ 1 − e − i ω ( 1 − k ^ ⋅ x ^ i j ) L c ] = 1 2 x ^ a x ^ b h ~ a b ( f ) e i ω ( t ∣ r ⃗ i − k ^ ⋅ r ⃗ i c ) e − i ω ( 1 − k ^ ⋅ x ^ i j ) L 2 c L c s i n c [ ω ( 1 − k ^ ⋅ x ^ i j ) L 2 c ] Δ ν ν = x ^ a x ^ b 2 ( 1 + k ^ ⋅ x ^ ) h ~ a b ( f ) e i ω ( t ∣ r ⃗ i − k ^ ⋅ r ⃗ i c ) [ 1 − e − i ω ( 1 − k ^ ⋅ x ^ ) L c ] = x ^ a x ^ b 2 ( 1 − k ^ ⋅ x ^ ) [ h ~ a b ( f ) e i ω ( t ∣ r ⃗ i − k ^ ⋅ r ⃗ i c ) − h ~ a b ( f ) e i ω ( t ∣ r ⃗ j − k ^ ⋅ r ⃗ j c ) ] \begin{aligned}
s_{ij} (f, t) &= \frac{1}{2}\hat{x}^a\hat{x}^b \tilde{h}_{ab}(f) e^{i\omega (t|_{\vec{r}_i} - \hat{k}\cdot\frac{\vec{r}_i}{c})} \small \frac{1}{i\omega (1 - \hat{k}\cdot\hat{x}_{ij})} \left[1 - e^{-i\omega (1 - \hat{k}\cdot\hat{x}_{ij})\frac{L}{c}}\right]\\
&= \frac{1}{2}\hat{x}^a\hat{x}^b \tilde{h}_{ab}(f) e^{i\omega (t|_{\vec{r}_i} - \hat{k}\cdot\frac{\vec{r}_i}{c})} e^{-i\omega (1- \hat{k} \cdot \hat{x}_{ij}) \frac{L}{2c} } ~ \small \frac{L}{c} ~ {\rm sinc}\left[\omega(1-\hat{k} \cdot \hat{x}_{ij}) {\textstyle \frac{L}{2c}}\right]\\
\frac{\Delta \nu}{\nu} &= \frac{\hat{x}^a\hat{x}^b}{2 (1 + \hat{k}\cdot\hat{x})} \tilde{h}_{ab}(f) e^{i\omega (t|_{\vec{r}_i} - \hat{k}\cdot\frac{\vec{r}_i}{c})} \left[1 - e^{-i\omega (1 - \hat{k}\cdot\hat{x})\frac{L}{c}}\right]\\
& = \frac{\hat{x}^a\hat{x}^b}{2(1 - \hat{k}\cdot\hat{x})} \left[\tilde{h}_{ab}(f) e^{i\omega (t|_{\vec{r}_i} - \hat{k}\cdot\frac{\vec{r}_i}{c})} - \tilde{h}_{ab}(f) e^{i\omega (t|_{\vec{r}_j} - \hat{k}\cdot\frac{\vec{r}_j}{c}) } \right]
\end{aligned} s i j ( f , t ) ν Δ ν = 2 1 x ^ a x ^ b h ~ a b ( f ) e i ω ( t ∣ r i − k ^ ⋅ c r i ) i ω ( 1 − k ^ ⋅ x ^ i j ) 1 [ 1 − e − i ω ( 1 − k ^ ⋅ x ^ i j ) c L ] = 2 1 x ^ a x ^ b h ~ a b ( f ) e i ω ( t ∣ r i − k ^ ⋅ c r i ) e − i ω ( 1 − k ^ ⋅ x ^ i j ) 2 c L c L s i n c [ ω ( 1 − k ^ ⋅ x ^ i j ) 2 c L ] = 2 ( 1 + k ^ ⋅ x ^ ) x ^ a x ^ b h ~ a b ( f ) e i ω ( t ∣ r i − k ^ ⋅ c r i ) [ 1 − e − i ω ( 1 − k ^ ⋅ x ^ ) c L ] = 2 ( 1 − k ^ ⋅ x ^ ) x ^ a x ^ b [ h ~ a b ( f ) e i ω ( t ∣ r i − k ^ ⋅ c r i ) − h ~ a b ( f ) e i ω ( t ∣ r j − k ^ ⋅ c r j ) ]
s ~ i j ( f ) = 1 2 x ^ a x ^ b h ~ a b ( f ) e − i ω k ^ ⋅ r ⃗ i c 1 i ω ( 1 − k ^ ⋅ x ^ i j ) [ 1 − e − i ω ( 1 − k ^ ⋅ x ^ i j ) L c ] = 1 2 x ^ a x ^ b h ~ a b ( f ) e − i ω k ^ ⋅ r ⃗ i c e − i ω ( 1 − k ^ ⋅ x ^ i j ) L 2 c L c s i n c [ ω ( 1 − k ^ ⋅ x ^ i j ) L 2 c ] y ~ i j ( f ) = x ^ a x ^ b 2 ( 1 + k ^ ⋅ x ^ ) h ~ a b ( f ) e − i ω k ^ ⋅ r ⃗ i c [ 1 − e − i ω ( 1 − k ^ ⋅ x ^ ) L c ] = x ^ a x ^ b 2 ( 1 − k ^ ⋅ x ^ ) h ~ a b ( f ) [ e − i ω k ^ ⋅ r ⃗ i c − e − i ω ( L c + k ^ ⋅ r ⃗ j c ) ] \begin{aligned}
\tilde{s}_{ij} (f) &= \frac{1}{2}\hat{x}^a\hat{x}^b \tilde{h}_{ab}(f) e^{-i\omega \hat{k}\cdot\frac{\vec{r}_i}{c}} \small \frac{1}{i\omega (1 - \hat{k}\cdot\hat{x}_{ij})} \left[1 - e^{-i\omega (1 - \hat{k}\cdot\hat{x}_{ij})\frac{L}{c}}\right]\\
&= \frac{1}{2}\hat{x}^a\hat{x}^b \tilde{h}_{ab}(f) e^{-i\omega \hat{k}\cdot\frac{\vec{r}_i}{c}} e^{-i\omega (1- \hat{k} \cdot \hat{x}_{ij}) \frac{L}{2c} } ~ \small \frac{L}{c} ~ {\rm sinc}\left[\omega(1-\hat{k} \cdot \hat{x}_{ij}) {\textstyle \frac{L}{2c}}\right]\\
\tilde{y}_{ij}(f) &= \frac{\hat{x}^a\hat{x}^b}{2 (1 + \hat{k}\cdot\hat{x})} \tilde{h}_{ab}(f) e^{-i\omega \hat{k}\cdot\frac{\vec{r}_i}{c}} \left[1 - e^{-i\omega (1 - \hat{k}\cdot\hat{x})\frac{L}{c}}\right]\\
& = \frac{\hat{x}^a\hat{x}^b}{2(1 - \hat{k}\cdot\hat{x})} \tilde{h}_{ab}(f) \left[e^{-i\omega \hat{k}\cdot\frac{\vec{r}_i}{c}} - e^{-i\omega ( \frac{L}{c} + \hat{k}\cdot\frac{\vec{r}_j}{c}) } \right]
\end{aligned} s ~ i j ( f ) y ~ i j ( f ) = 2 1 x ^ a x ^ b h ~ a b ( f ) e − i ω k ^ ⋅ c r i i ω ( 1 − k ^ ⋅ x ^ i j ) 1 [ 1 − e − i ω ( 1 − k ^ ⋅ x ^ i j ) c L ] = 2 1 x ^ a x ^ b h ~ a b ( f ) e − i ω k ^ ⋅ c r i e − i ω ( 1 − k ^ ⋅ x ^ i j ) 2 c L c L s i n c [ ω ( 1 − k ^ ⋅ x ^ i j ) 2 c L ] = 2 ( 1 + k ^ ⋅ x ^ ) x ^ a x ^ b h ~ a b ( f ) e − i ω k ^ ⋅ c r i [ 1 − e − i ω ( 1 − k ^ ⋅ x ^ ) c L ] = 2 ( 1 − k ^ ⋅ x ^ ) x ^ a x ^ b h ~ a b ( f ) [ e − i ω k ^ ⋅ c r i − e − i ω ( c L + k ^ ⋅ c r j ) ]
X = [ D 31 D 13 D 21 η 12 + D 31 D 13 η 21 + D 31 η 13 + η 31 ] − [ η 21 + D 21 η 12 + D 21 D 12 η 31 + D 21 D 12 D 31 η 13 ] = ( D 31 D 13 D 21 − D 21 ) η 12 + ( D 31 D 13 − 1 ) η 21 + ( D 31 − D 21 D 12 D 31 ) η 13 + ( 1 − D 21 D 12 ) η 31 \begin{aligned}
X = & [\mathcal{D}_{31} \mathcal{D}_{13} \mathcal{D}_{21} \eta_{12} +\mathcal{D}_{31} \mathcal{D}_{13} \eta_{21} +\mathcal{D}_{31} \eta_{13} + \eta_{31}]\\
& - [\eta_{21} +\mathcal{D}_{21} \eta_{12} +\mathcal{D}_{21} \mathcal{D}_{12} \eta_{31} +\mathcal{D}_{21} \mathcal{D}_{12} \mathcal{D}_{31} \eta_{13}]\\
= & (\mathcal{D}_{31} \mathcal{D}_{13} \mathcal{D}_{21} -\mathcal{D}_{21}) \eta_{12} + (\mathcal{D}_{31} \mathcal{D}_{13} - 1) \eta_{21} \\
& + (\mathcal{D}_{31} -\mathcal{D}_{21} \mathcal{D}_{12} \mathcal{D}_{31}) \eta_{13} + (1 -\mathcal{D}_{21} \mathcal{D}_{12}) \eta_{31}
\end{aligned} X = = [ D 3 1 D 1 3 D 2 1 η 1 2 + D 3 1 D 1 3 η 2 1 + D 3 1 η 1 3 + η 3 1 ] − [ η 2 1 + D 2 1 η 1 2 + D 2 1 D 1 2 η 3 1 + D 2 1 D 1 2 D 3 1 η 1 3 ] ( D 3 1 D 1 3 D 2 1 − D 2 1 ) η 1 2 + ( D 3 1 D 1 3 − 1 ) η 2 1 + ( D 3 1 − D 2 1 D 1 2 D 3 1 ) η 1 3 + ( 1 − D 2 1 D 1 2 ) η 3 1
D i j \mathcal{D}_{ij} D i j Δ i j \Delta_{ij} Δ i j Δ i j = e − i ω L i j c \Delta_{ij} = e^{-i\omega\frac{L_{ij}}{c}} Δ i j = e − i ω c L i j Δ i j = e i ω L i j c \Delta_{ij} = e^{i\omega\frac{L_{ij}}{c}} Δ i j = e i ω c L i j
s ~ X ( f ) = ( Δ 21 Δ 13 Δ 31 − Δ 21 ) s ~ 12 + ( Δ 13 Δ 31 − 1 ) s ~ 21 + ( Δ 31 − Δ 31 Δ 12 Δ 21 ) s ~ 13 + ( 1 − Δ 12 Δ 21 ) s ~ 31 y ~ X ( f ) = ( Δ 21 Δ 13 Δ 31 − Δ 21 ) y ~ 12 + ( Δ 13 Δ 31 − 1 ) y ~ 21 + ( Δ 31 − Δ 31 Δ 12 Δ 21 ) y ~ 13 + ( 1 − Δ 12 Δ 21 ) y ~ 31 \begin{aligned}
\tilde{s}_X(f) =& (\Delta_{21} \Delta_{13} \Delta_{31} - \Delta_{21}) \tilde{s}_{12} + (\Delta_{13} \Delta_{31} - 1) \tilde{s}_{21}\\
& + (\Delta_{31} - \Delta_{31} \Delta_{12} \Delta_{21})\tilde{s}_{13} + (1 - \Delta_{12} \Delta_{21}) \tilde{s}_{31}\\
\tilde{y}_X(f) =& (\Delta_{21} \Delta_{13} \Delta_{31} - \Delta_{21}) \tilde{y}_{12} + (\Delta_{13} \Delta_{31} - 1) \tilde{y}_{21}\\
& + (\Delta_{31} - \Delta_{31} \Delta_{12} \Delta_{21})\tilde{y}_{13} + (1 - \Delta_{12} \Delta_{21}) \tilde{y}_{31}
\end{aligned} s ~ X ( f ) = y ~ X ( f ) = ( Δ 2 1 Δ 1 3 Δ 3 1 − Δ 2 1 ) s ~ 1 2 + ( Δ 1 3 Δ 3 1 − 1 ) s ~ 2 1 + ( Δ 3 1 − Δ 3 1 Δ 1 2 Δ 2 1 ) s ~ 1 3 + ( 1 − Δ 1 2 Δ 2 1 ) s ~ 3 1 ( Δ 2 1 Δ 1 3 Δ 3 1 − Δ 2 1 ) y ~ 1 2 + ( Δ 1 3 Δ 3 1 − 1 ) y ~ 2 1 + ( Δ 3 1 − Δ 3 1 Δ 1 2 Δ 2 1 ) y ~ 1 3 + ( 1 − Δ 1 2 Δ 2 1 ) y ~ 3 1
F i j P ( f ) = 1 2 x ^ a x ^ b e a b P e − i ω k ^ ⋅ r ⃗ i c 1 i ω ( 1 − k ^ ⋅ x ^ i j ) [ 1 − e − i ω ( 1 − k ^ ⋅ x ^ i j ) L c ] = 1 2 x ^ a x ^ b h ~ a b ( f ) e − i ω k ^ ⋅ r ⃗ i c e − i ω ( 1 − k ^ ⋅ x ^ i j ) L 2 c L c s i n c [ ω ( 1 − k ^ ⋅ x ^ i j ) L 2 c ] F i j P ( f ) = x ^ a x ^ b 2 ( 1 + k ^ ⋅ x ^ ) h ~ a b ( f ) e − i ω k ^ ⋅ r ⃗ i c [ 1 − e − i ω ( 1 − k ^ ⋅ x ^ ) L c ] = x ^ a x ^ b e a b P 2 ( 1 − k ^ ⋅ x ^ ) [ e − i ω k ^ ⋅ r ⃗ i c − e − i ω ( L c + k ^ ⋅ r ⃗ j c ) ] \begin{aligned}
F^P_{ij} (f) &= \frac{1}{2}\hat{x}^a\hat{x}^b e^P_{ab} e^{-i\omega \hat{k}\cdot\frac{\vec{r}_i}{c}} \small \frac{1}{i\omega (1 - \hat{k}\cdot\hat{x}_{ij})} \left[1 - e^{-i\omega (1 - \hat{k}\cdot\hat{x}_{ij})\frac{L}{c}}\right]\\
&= \frac{1}{2}\hat{x}^a\hat{x}^b \tilde{h}_{ab}(f) e^{-i\omega \hat{k}\cdot\frac{\vec{r}_i}{c}} e^{-i\omega (1- \hat{k} \cdot \hat{x}_{ij}) \frac{L}{2c} } ~ \small \frac{L}{c} ~ {\rm sinc}\left[\omega(1-\hat{k} \cdot \hat{x}_{ij}) {\textstyle \frac{L}{2c}}\right]\\
F^P_{ij}(f) &= \frac{\hat{x}^a\hat{x}^b}{2 (1 + \hat{k}\cdot\hat{x})} \tilde{h}_{ab}(f) e^{-i\omega \hat{k}\cdot\frac{\vec{r}_i}{c}} \left[1 - e^{-i\omega (1 - \hat{k}\cdot\hat{x})\frac{L}{c}}\right]\\
& = \frac{\hat{x}^a\hat{x}^b e^P_{ab}}{2(1 - \hat{k}\cdot\hat{x})} \left[ e^{-i\omega \hat{k}\cdot\frac{\vec{r}_i}{c}} - e^{-i\omega ( \frac{L}{c} + \hat{k}\cdot\frac{\vec{r}_j}{c}) } \right]
\end{aligned} F i j P ( f ) F i j P ( f ) = 2 1 x ^ a x ^ b e a b P e − i ω k ^ ⋅ c r i i ω ( 1 − k ^ ⋅ x ^ i j ) 1 [ 1 − e − i ω ( 1 − k ^ ⋅ x ^ i j ) c L ] = 2 1 x ^ a x ^ b h ~ a b ( f ) e − i ω k ^ ⋅ c r i e − i ω ( 1 − k ^ ⋅ x ^ i j ) 2 c L c L s i n c [ ω ( 1 − k ^ ⋅ x ^ i j ) 2 c L ] = 2 ( 1 + k ^ ⋅ x ^ ) x ^ a x ^ b h ~ a b ( f ) e − i ω k ^ ⋅ c r i [ 1 − e − i ω ( 1 − k ^ ⋅ x ^ ) c L ] = 2 ( 1 − k ^ ⋅ x ^ ) x ^ a x ^ b e a b P [ e − i ω k ^ ⋅ c r i − e − i ω ( c L + k ^ ⋅ c r j ) ]
F X P ( f ) = ( Δ 21 Δ 13 Δ 31 − Δ 21 ) F 12 P + ( Δ 13 Δ 31 − 1 ) F 21 P + ( Δ 31 − Δ 31 Δ 12 Δ 21 ) F 13 P + ( 1 − Δ 12 Δ 21 ) F 31 P \begin{aligned}
F^P_X(f) =& (\Delta_{21} \Delta_{13} \Delta_{31} - \Delta_{21}) F^P_{12} + (\Delta_{13} \Delta_{31} - 1) F^P_{21}\\
& + (\Delta_{31} - \Delta_{31} \Delta_{12} \Delta_{21})F^P_{13} + (1 - \Delta_{12} \Delta_{21}) F^P_{31}
\end{aligned} F X P ( f ) = ( Δ 2 1 Δ 1 3 Δ 3 1 − Δ 2 1 ) F 1 2 P + ( Δ 1 3 Δ 3 1 − 1 ) F 2 1 P + ( Δ 3 1 − Δ 3 1 Δ 1 2 Δ 2 1 ) F 1 3 P + ( 1 − Δ 1 2 Δ 2 1 ) F 3 1 P
Seto 2002η 12 , η 13 \eta_{12}, \eta_{13} η 1 2 , η 1 3 η 31 + Δ 31 η 13 , η 21 + Δ 21 η 12 \eta_{31} + \Delta_{31}\eta_{13}, \eta_{21} + \Delta_{21}\eta_{12} η 3 1 + Δ 3 1 η 1 3 , η 2 1 + Δ 2 1 η 1 2 η 31 + Δ 31 η 13 − ( η 21 + Δ 21 η 12 ) \eta_{31} + \Delta_{31}\eta_{13} - (\eta_{21} + \Delta_{21}\eta_{12}) η 3 1 + Δ 3 1 η 1 3 − ( η 2 1 + Δ 2 1 η 1 2 ) Δ = e − i ω L c = e − i x \Delta = e^{-i\omega\frac{L}{c}}= e^{-i x} Δ = e − i ω c L = e − i x
[ η 31 + Δ 31 η 13 − ( η 21 + Δ 21 η 12 ) ] − Δ Δ [ η 31 + Δ 31 η 13 − ( η 21 + Δ 21 η 12 ) ] = ( 1 − e − i 2 x ) [ η 31 + Δ 31 η 13 − ( η 21 + Δ 21 η 12 ) ] \begin{aligned}
&\Big[\eta_{31} + \Delta_{31}\eta_{13} - (\eta_{21} + \Delta_{21}\eta_{12})\Big] - \Delta\Delta\Big[\eta_{31} + \Delta_{31}\eta_{13} - (\eta_{21} + \Delta_{21}\eta_{12})\Big]\\
&= \left(1-e^{-i 2 x}\right)\Big[\eta_{31} + \Delta_{31}\eta_{13} - (\eta_{21} + \Delta_{21}\eta_{12})\Big]
\end{aligned}
[ η 3 1 + Δ 3 1 η 1 3 − ( η 2 1 + Δ 2 1 η 1 2 ) ] − Δ Δ [ η 3 1 + Δ 3 1 η 1 3 − ( η 2 1 + Δ 2 1 η 1 2 ) ] = ( 1 − e − i 2 x ) [ η 3 1 + Δ 3 1 η 1 3 − ( η 2 1 + Δ 2 1 η 1 2 ) ]
( 1 − e − i 2 x ) 2 1 2 [ r ^ 12 a r ^ 12 b − r ^ 13 a r ^ 13 b ] h ~ a b ( f ) \left(1-e^{-i 2 x}\right)^2 ~ \frac{1}{2}\left[\hat{r}^a_{12}\hat{r}^b_{12} - \hat{r}^a_{13}\hat{r}^b_{13}\right] \tilde{h}_{ab}(f)
( 1 − e − i 2 x ) 2 2 1 [ r ^ 1 2 a r ^ 1 2 b − r ^ 1 3 a r ^ 1 3 b ] h ~ a b ( f )
其中( 1 − e − i 2 x ) 2 (1-e^{-i 2 x})^2 ( 1 − e − i 2 x ) 2 ∼ 4 x 2 \sim 4 x^2 ∼ 4 x 2
1 − e − i 2 x = e − i x ( e i x − e − i x ) = 2 i e − i x sin x 1-e^{-i 2 x} = e^{-i x}\left(e^{i x} - e^{-i x}\right) = 2 ~i~ e^{-i x} \sin x
1 − e − i 2 x = e − i x ( e i x − e − i x ) = 2 i e − i x sin x
− 4 e − i 2 x sin 2 x r ^ 12 a r ^ 12 b − r ^ 13 a r ^ 13 b 2 h ~ a b ( f ) -4 e^{-i 2x} \sin^2 x ~ \frac{\hat{r}^a_{12}\hat{r}^b_{12} - \hat{r}^a_{13}\hat{r}^b_{13}}{2} \tilde{h}_{ab}(f)
− 4 e − i 2 x sin 2 x 2 r ^ 1 2 a r ^ 1 2 b − r ^ 1 3 a r ^ 1 3 b h ~ a b ( f )
e − i 2 x sin 2 x ∼ e − i x x sin x ∼ sin 2 x ∼ x sin x ∼ x 2 e^{-i 2x} \sin^2 x \sim e^{-i x} x \sin x \sim \sin^2 x \sim x \sin x \sim x^2
e − i 2 x sin 2 x ∼ e − i x x sin x ∼ sin 2 x ∼ x sin x ∼ x 2
Cornish & Shuman 2020k ^ \hat{k} k ^ x x x x x x f ∗ = c / 2 π L , x = 2 π f L / c f_* = c/2 \pi L, x = 2\pi f L/c f ∗ = c / 2 π L , x = 2 π f L / c
T ( f ) = s i n c ( x / 2 ) e − i 3 x / 2 + s i n c ( x / 2 ) e − i x / 2 = s i n c ( x / 2 ) e − i x ( e − i x / 2 + e i x / 2 ) = sin ( x / 2 ) x / 2 e − i x 2 cos ( x / 2 ) = 2 sin x x e − i x → 2 \begin{aligned}
\mathcal{T}(f) &= {\rm sinc} (x/2)~ e^{-i3x/2} + {\rm sinc}(x/2)~e^{-ix/2}\\
& = {\rm sinc}(x/2) e^{-ix} \left(e^{-ix/2} + e^{ix/2} \right)\\
& = \frac{\sin(x/2)}{x/2} e^{-ix} ~ 2\cos(x/2)\\
& = 2 \frac{\sin x}{x} e^{-ix} ~~~~~ {\color{red} \rightarrow 2}\\
\end{aligned} T ( f ) = s i n c ( x / 2 ) e − i 3 x / 2 + s i n c ( x / 2 ) e − i x / 2 = s i n c ( x / 2 ) e − i x ( e − i x / 2 + e i x / 2 ) = x / 2 sin ( x / 2 ) e − i x 2 cos ( x / 2 ) = 2 x sin x e − i x → 2
X ( f ) = − x e − i x sin x [ r ^ 12 a r ^ 12 b − r ^ 13 a r ^ 13 b ] h ~ a b ( f ) T ( f ) = − x e − i x sin x [ r ^ 12 a r ^ 12 b − r ^ 13 a r ^ 13 b ] h ~ a b ( f ) 2 sin x x e − i x = − 2 e − i 2 x sin 2 x [ r ^ 12 a r ^ 12 b − r ^ 13 a r ^ 13 b ] h ~ a b ( f ) \begin{aligned}
X(f) &= -x ~ e^{-ix} \sin x \left[\hat{r}^a_{12}\hat{r}^b_{12} - \hat{r}^a_{13}\hat{r}^b_{13}\right]\tilde{h}_{ab}(f) ~ \mathcal{T}(f) \\
&= -x ~ e^{-ix} \sin x \left[\hat{r}^a_{12}\hat{r}^b_{12} - \hat{r}^a_{13}\hat{r}^b_{13}\right]\tilde{h}_{ab}(f) ~ 2 \frac{\sin x}{x} e^{-ix} \\
&= - 2 e^{-i 2 x} \sin^2 x \left[\hat{r}^a_{12}\hat{r}^b_{12} - \hat{r}^a_{13}\hat{r}^b_{13}\right]\tilde{h}_{ab}(f) \\
\end{aligned} X ( f ) = − x e − i x sin x [ r ^ 1 2 a r ^ 1 2 b − r ^ 1 3 a r ^ 1 3 b ] h ~ a b ( f ) T ( f ) = − x e − i x sin x [ r ^ 1 2 a r ^ 1 2 b − r ^ 1 3 a r ^ 1 3 b ] h ~ a b ( f ) 2 x sin x e − i x = − 2 e − i 2 x sin 2 x [ r ^ 1 2 a r ^ 1 2 b − r ^ 1 3 a r ^ 1 3 b ] h ~ a b ( f )
X ( f ) ≈ − 2 sin 2 x [ r ^ 12 a r ^ 12 b − r ^ 13 a r ^ 13 b ] h ~ a b ( f ) ≈ − 2 x sin x [ r ^ 12 a r ^ 12 b − r ^ 13 a r ^ 13 b ] h ~ a b ( f ) ≈ 4 x sin x 3 2 x ^ a x ^ b − y ^ a y ^ b 2 h ~ a b ( f ) \begin{aligned}
X(f) &\approx - 2 \sin^2 x \left[\hat{r}^a_{12}\hat{r}^b_{12} - \hat{r}^a_{13}\hat{r}^b_{13}\right]\tilde{h}_{ab}(f) \\
&\approx - 2 x \sin x \left[\hat{r}^a_{12}\hat{r}^b_{12} - \hat{r}^a_{13}\hat{r}^b_{13}\right]\tilde{h}_{ab}(f) \\
&\approx 4 x \sin x \frac{\sqrt{3}}{2} \frac{\hat{x}^a\hat{x}^b - \hat{y}^a\hat{y}^b}{2}\tilde{h}_{ab}(f) \\
\end{aligned} X ( f ) ≈ − 2 sin 2 x [ r ^ 1 2 a r ^ 1 2 b − r ^ 1 3 a r ^ 1 3 b ] h ~ a b ( f ) ≈ − 2 x sin x [ r ^ 1 2 a r ^ 1 2 b − r ^ 1 3 a r ^ 1 3 b ] h ~ a b ( f ) ≈ 4 x sin x 2 3 2 x ^ a x ^ b − y ^ a y ^ b h ~ a b ( f )
Babak et al. 2021
X ( f ) ≈ 4 ω L sin ( ω L ) 3 2 ( F + h ~ + + F × h ~ × ) \begin{aligned}
X(f) &\approx 4\omega L \sin(\omega L) \frac{\sqrt{3}}{2}(F_+\tilde{h}_+ + F_\times\tilde{h}_\times)\\
\end{aligned} X ( f ) ≈ 4 ω L sin ( ω L ) 2 3 ( F + h ~ + + F × h ~ × )
与上面Cornish & Shuman 2020的结果对比，F + F_+ F +
E ( f ) ≈ 2 x sin x 3 2 x ^ a x ^ b − y ^ a y ^ b 2 h ~ a b ( f ) \begin{aligned}
E(f) &\approx 2x \sin x \frac{3}{\sqrt{2}} \frac{\hat{x}^a\hat{x}^b - \hat{y}^a\hat{y}^b}{2}\tilde{h}_{ab}(f)\\
\end{aligned} E ( f ) ≈ 2 x sin x 2 3 2 x ^ a x ^ b − y ^ a y ^ b h ~ a b ( f )
Seto 2006 （少了2倍？）
E ≈ 3 2 x 2 x ^ a x ^ b − y ^ a y ^ b 2 h ~ a b ( f ) \begin{aligned}
E &\approx \frac{3}{\sqrt{2}} x^2 \frac{\hat{x}^a\hat{x}^b - \hat{y}^a\hat{y}^b}{2}\tilde{h}_{ab}(f) \\
\end{aligned} E ≈ 2 3 x 2 2 x ^ a x ^ b − y ^ a y ^ b h ~ a b ( f )
Krolak et al. 2004
LDC(2a), Vallisneri & Galley 2012
S X = 16 sin 2 x [ S O M S + 2 ( 1 + cos 2 x ) S a c c ] , S X Y = − 8 sin 2 x cos x ( S O M S + 4 S a c c ) S_X = 16 \sin^2 x\left[ S_{\rm OMS} + 2(1+\cos^2 x)S_{\rm acc}\right], ~~~ S_{XY} = -8\sin^2 x \cos x \left( {S_{\rm OMS} + 4 S_{\rm acc}} \right)
S X = 1 6 sin 2 x [ S O M S + 2 ( 1 + cos 2 x ) S a c c ] , S X Y = − 8 sin 2 x cos x ( S O M S + 4 S a c c )
A = Z − X 2 , E = X − 2 Y + Z 6 , T = X + Y + Z 3 A = \frac{Z - X}{\sqrt{2}}, ~~~ E = \frac{X - 2Y + Z}{\sqrt{6}}, ~~~ T = \frac{X + Y + Z}{\sqrt{3}}
A = 2 Z − X , E = 6 X − 2 Y + Z , T = 3 X + Y + Z
最早出现于Prince et al. 2002
S A = 1 2 ( S X + S Z − S X Z − S Z X ) = S X − S X Y S_A = \frac{1}{2}\left(S_X + S_Z - S_{XZ} - S_{ZX}\right) = S_X - S_{XY}
S A = 2 1 ( S X + S Z − S X Z − S Z X ) = S X − S X Y
S E = S X − S X Y , S T = S X + 2 S X Y S_E = S_X - S_{XY}, ~~~~~~ S_T = S_X + 2S_{XY}
S E = S X − S X Y , S T = S X + 2 S X Y
最终有：
S A = S E = 16 sin 2 x [ ( 1 + 1 2 cos x ) S O M S + 2 ( 1 + cos x + cos 2 x ) S a c c ] S_A = S_E = 16\sin^2 x\left[(1+\frac{1}{2}\cos x)S_{\rm OMS} + 2(1+\cos x + \cos^2 x)S_{\rm acc}\right]
S A = S E = 1 6 sin 2 x [ ( 1 + 2 1 cos x ) S O M S + 2 ( 1 + cos x + cos 2 x ) S a c c ]
S T = 16 sin 2 x [ ( 1 − cos x ) S O M S + 2 ( 1 − cos x ) 2 S a c c ] S_T = 16\sin^2 x\left[(1-\cos x)S_{\rm OMS} + 2(1-\cos x)^2 S_{\rm acc}\right]
S T = 1 6 sin 2 x [ ( 1 − cos x ) S O M S + 2 ( 1 − cos x ) 2 S a c c ]
对比Cornish 2002中的噪声谱
S n = 4 [ S O M S + 2 ( 1 + cos 2 x ) S a c c ] S_n = 4\left[S_{\rm OMS} + 2(1+\cos^2 x)S_{\rm acc}\right]
S n = 4 [ S O M S + 2 ( 1 + cos 2 x ) S a c c ]
少了因子( 2 sin x ) 2 (2\sin x)^2 ( 2 sin x ) 2 ∣ 1 − e − i 2 x ∣ ∼ 2 sin x |1-e^{-i2 x}| \sim 2 \sin x ∣ 1 − e − i 2 x ∣ ∼ 2 sin x
S n = 1 L 2 [ S O M S + 2 ( 1 + cos 2 x ) S a c c ] S_n = \frac{1}{L^2}\left[S_{\rm OMS} + 2(1+\cos^2 x)S_{\rm acc}\right]
S n = L 2 1 [ S O M S + 2 ( 1 + cos 2 x ) S a c c ]
如果将AE通道的光程变化噪声谱对应到应力，有：
S n = sin 2 x L 2 [ ( 1 + 1 2 cos x ) S O M S + 2 ( 1 + cos x + cos 2 x ) S a c c ] S_n = \frac{\sin^2 x}{L^2}\left[\left(1+\frac{1}{2}\cos x\right)S_{\rm OMS} + 2(1+\cos x + \cos^2 x)S_{\rm acc}\right]
S n = L 2 sin 2 x [ ( 1 + 2 1 cos x ) S O M S + 2 ( 1 + cos x + cos 2 x ) S a c c ]
Cornish & Shuman (2020)
h a b = h + ϵ a b + + h × ϵ a b × h_{ab} = h_+\epsilon_{ab}^+ + h_\times \epsilon_{ab}^\times
h a b = h + ϵ a b + + h × ϵ a b ×
h + = h 0 1 + cos 2 ι 2 cos Φ , h × = h 0 cos ι sin Φ h_+ = h_0 \frac{1+\cos^2\iota}{2} \cos \Phi, ~~~ h_\times = h_0 \cos\iota ~ \sin\Phi
h + = h 0 2 1 + cos 2 ι cos Φ , h × = h 0 cos ι sin Φ
h + = h 0 1 + cos 2 ι 2 e i Φ , h × = h 0 cos ι e i ( Φ − π 2 ) h_+ = h_0 \frac{1+\cos^2\iota}{2} e^{i\Phi}, ~~~ h_\times = h_0 \cos\iota ~ e^{i(\Phi-\frac{\pi}{2})}
h + = h 0 2 1 + cos 2 ι e i Φ , h × = h 0 cos ι e i ( Φ − 2 π )
h a b = h 0 e i Φ [ 1 + cos 2 ι 2 ϵ a b + − i cos ι ϵ a b × ] = h ( t ) [ A + ϵ a b + + i A × ϵ a b × ] h_{ab} = h_0 e^{i\Phi} \left[ \frac{1+\cos^2\iota}{2} \epsilon_{ab}^+ - i \cos\iota ~ \epsilon_{ab}^\times\right] = h(t) \left[ A_+ \epsilon_{ab}^+ + i A_\times \epsilon_{ab}^\times\right]
h a b = h 0 e i Φ [ 2 1 + cos 2 ι ϵ a b + − i cos ι ϵ a b × ] = h ( t ) [ A + ϵ a b + + i A × ϵ a b × ]
以δ ν ν 0 \frac{\delta \nu}{\nu_0} ν 0 δ ν δ L L \frac{\delta L}{L} L δ L 4 f / f ∗ = 4 x 4f/f_* = 4x 4 f / f ∗ = 4 x
X ( f ) = − 2 x sin x [ r ^ 12 a r ^ 12 b − r ^ 13 a r ^ 13 b ] h ~ a b ( f ) X(f) = - 2x \sin x \left[\hat{r}^a_{12}\hat{r}^b_{12} - \hat{r}^a_{13}\hat{r}^b_{13}\right] \tilde{h}_{ab}(f)
X ( f ) = − 2 x sin x [ r ^ 1 2 a r ^ 1 2 b − r ^ 1 3 a r ^ 1 3 b ] h ~ a b ( f )
Y ( f ) = − 2 x sin x [ r ^ 23 a r ^ 23 b − r ^ 21 a r ^ 21 b ] h ~ a b ( f ) Y(f) = - 2x \sin x \left[\hat{r}^a_{23}\hat{r}^b_{23} - \hat{r}^a_{21}\hat{r}^b_{21}\right] \tilde{h}_{ab}(f)
Y ( f ) = − 2 x sin x [ r ^ 2 3 a r ^ 2 3 b − r ^ 2 1 a r ^ 2 1 b ] h ~ a b ( f )
Z ( f ) = − 2 x sin x [ r ^ 31 a r ^ 31 b − r ^ 32 a r ^ 32 b ] h ~ a b ( f ) Z(f) = - 2x\sin x \left[\hat{r}^a_{31}\hat{r}^b_{31} - \hat{r}^a_{32}\hat{r}^b_{32}\right] \tilde{h}_{ab}(f)
Z ( f ) = − 2 x sin x [ r ^ 3 1 a r ^ 3 1 b − r ^ 3 2 a r ^ 3 2 b ] h ~ a b ( f )
Z − X = − 2 x sin x [ r ^ 31 a r ^ 31 b − r ^ 32 a r ^ 32 b − r ^ 12 a r ^ 12 b + r ^ 13 a r ^ 13 b ] h ~ a b ( f ) = − 2 x sin x 3 2 [ y ^ a y ^ b − x ^ a x ^ b ] h ~ a b ( f ) X − 2 Y + Z = − 2 x sin x [ r ^ 12 a r ^ 12 b − r ^ 13 a r ^ 13 b − 2 r ^ 23 a r ^ 23 b + 2 r ^ 21 a r ^ 21 b + r ^ 31 a r ^ 31 b − r ^ 32 a r ^ 32 b ] h ~ a b ( f ) = − 2 x sin x 3 [ r ^ 21 a r ^ 21 b − r ^ 23 a r ^ 23 b ] h ~ a b ( f ) X + Y + Z = − 2 x sin x [ r ^ 12 a r ^ 12 b − r ^ 13 a r ^ 13 b + r ^ 23 a r ^ 23 b − r ^ 21 a r ^ 21 b + r ^ 31 a r ^ 31 b − r ^ 32 a r ^ 32 b ] h ~ a b ( f ) = 0 \footnotesize
\begin{aligned}
Z - X &= - 2x\sin x \left[\hat{r}^a_{31}\hat{r}^b_{31} - \hat{r}^a_{32}\hat{r}^b_{32} - \hat{r}^a_{12}\hat{r}^b_{12} + \hat{r}^a_{13}\hat{r}^b_{13}\right] \tilde{h}_{ab}(f)\\
&= - 2x\sin x ~\frac{3}{2}~\left[\hat{y}^a\hat{y}^b - \hat{x}^a\hat{x}^b\right] \tilde{h}_{ab}(f)\\
X - 2Y + Z &= - 2x\sin x \left[ \hat{r}^a_{12}\hat{r}^b_{12} - \hat{r}^a_{13}\hat{r}^b_{13} - 2\hat{r}^a_{23}\hat{r}^b_{23} + 2\hat{r}^a_{21}\hat{r}^b_{21} + \hat{r}^a_{31}\hat{r}^b_{31} - \hat{r}^a_{32}\hat{r}^b_{32}\right] \tilde{h}_{ab}(f)\\
&= - 2x\sin x ~3~\left[\hat{r}^a_{21}\hat{r}^b_{21} - \hat{r}^a_{23}\hat{r}^b_{23}\right] \tilde{h}_{ab}(f)\\
X + Y + Z =& -2x\sin x \left[ \hat{r}^a_{12}\hat{r}^b_{12} - \hat{r}^a_{13}\hat{r}^b_{13} + \hat{r}^a_{23}\hat{r}^b_{23} - \hat{r}^a_{21}\hat{r}^b_{21} + \hat{r}^a_{31}\hat{r}^b_{31} - \hat{r}^a_{32}\hat{r}^b_{32}\right] \tilde{h}_{ab}(f) = 0
\end{aligned} Z − X X − 2 Y + Z X + Y + Z = = − 2 x sin x [ r ^ 3 1 a r ^ 3 1 b − r ^ 3 2 a r ^ 3 2 b − r ^ 1 2 a r ^ 1 2 b + r ^ 1 3 a r ^ 1 3 b ] h ~ a b ( f ) = − 2 x sin x 2 3 [ y ^ a y ^ b − x ^ a x ^ b ] h ~ a b ( f ) = − 2 x sin x [ r ^ 1 2 a r ^ 1 2 b − r ^ 1 3 a r ^ 1 3 b − 2 r ^ 2 3 a r ^ 2 3 b + 2 r ^ 2 1 a r ^ 2 1 b + r ^ 3 1 a r ^ 3 1 b − r ^ 3 2 a r ^ 3 2 b ] h ~ a b ( f ) = − 2 x sin x 3 [ r ^ 2 1 a r ^ 2 1 b − r ^ 2 3 a r ^ 2 3 b ] h ~ a b ( f ) − 2 x sin x [ r ^ 1 2 a r ^ 1 2 b − r ^ 1 3 a r ^ 1 3 b + r ^ 2 3 a r ^ 2 3 b − r ^ 2 1 a r ^ 2 1 b + r ^ 3 1 a r ^ 3 1 b − r ^ 3 2 a r ^ 3 2 b ] h ~ a b ( f ) = 0
Z − X 2 = 3 2 x sin x x ^ a x ^ b − y ^ a y ^ b 2 h ~ a b ( f ) X − 2 Y + Z 6 = 3 2 x sin x x ^ a y ^ b + y ^ a x ^ b 2 h ~ a b ( f ) S A = S E = 16 sin 2 x [ ( 1 + 1 2 cos x ) S O M S + 2 ( 1 + cos x + cos 2 x ) S a c c ] \begin{aligned}
\frac{Z - X}{\sqrt{2}} &= 3\sqrt{2} ~ x\sin x \frac{\hat{x}^a\hat{x}^b - \hat{y}^a\hat{y}^b}{2} \tilde{h}_{ab}(f)\\
\frac{X - 2Y + Z}{\sqrt{6}} &= 3\sqrt{2} ~ x\sin x \frac{\hat{x}^a\hat{y}^b + \hat{y}^a\hat{x}^b}{2} \tilde{h}_{ab}(f) \\
S_A = S_E &= 16\sin^2 x\left[(1+\frac{1}{2}\cos x)S_{\rm OMS} + 2(1+\cos x + \cos^2 x)S_{\rm acc}\right]
\end{aligned} 2 Z − X 6 X − 2 Y + Z S A = S E = 3 2 x sin x 2 x ^ a x ^ b − y ^ a y ^ b h ~ a b ( f ) = 3 2 x sin x 2 x ^ a y ^ b + y ^ a x ^ b h ~ a b ( f ) = 1 6 sin 2 x [ ( 1 + 2 1 cos x ) S O M S + 2 ( 1 + cos x + cos 2 x ) S a c c ]
这种归一化下，信号放大了约∼ 3 / 2 ∼ 1.2 \sim \sqrt{3/2} \sim 1.2 ∼ 3 / 2 ∼ 1 . 2 x = 0 x=0 x = 0 3 / 2 3/2 3 / 2
E = Z − Y 3 , A = 2 X − Y − Z 3 , T = X + Y + Z 3 E = \frac{Z - Y}{\sqrt{3}}, ~~~ A = \frac{2X - Y - Z}{3}, ~~~T = \frac{X + Y + Z}{3}
E = 3 Z − Y , A = 3 2 X − Y − Z , T = 3 X + Y + Z
最早出现于Adams & Cornish 2010
X ( f ) = − 2 x sin x [ r ^ 12 a r ^ 12 b − r ^ 13 a r ^ 13 b ] h ~ a b ( f ) = 2 x sin x sin α [ x ^ a y ^ b + y ^ a x ^ b ] h ~ a b ( f ) = 2 3 x sin x x ^ ′ a x ^ ′ b − y ^ ′ a y ^ ′ b 2 h ~ a b ( f ) \begin{aligned}
X(f) &= - 2x\sin x \left[\hat{r}^a_{12}\hat{r}^b_{12} - \hat{r}^a_{13}\hat{r}^b_{13}\right] \tilde{h}_{ab}(f)\\
% = 2x\sin x 2\sin\frac{\alpha}{2}\cos\frac{\alpha}{2} \left[\hat{x}^a\hat{y}^b + \hat{y}^a\hat{x}^b\right] \tilde{h}_{ab}(f)\\
&= 2x\sin x \sin \alpha \left[\hat{x}^a\hat{y}^b + \hat{y}^a\hat{x}^b\right] \tilde{h}_{ab}(f)\\
&= 2\sqrt{3}~ x\sin x \frac{\hat{x}'^a\hat{x}'^b - \hat{y}'^a\hat{y}'^b}{2} \tilde{h}_{ab}(f)\\
\end{aligned} X ( f ) = − 2 x sin x [ r ^ 1 2 a r ^ 1 2 b − r ^ 1 3 a r ^ 1 3 b ] h ~ a b ( f ) = 2 x sin x sin α [ x ^ a y ^ b + y ^ a x ^ b ] h ~ a b ( f ) = 2 3 x sin x 2 x ^ ′ a x ^ ′ b − y ^ ′ a y ^ ′ b h ~ a b ( f )
X − Y = − 2 x sin x [ r ^ 31 a r ^ 31 b − r ^ 32 a r ^ 32 b − r ^ 23 a r ^ 23 b + r ^ 21 a r ^ 21 b ] h ~ a b ( f ) = − 2 x sin x 3 2 [ y ^ a y ^ b − x ^ a x ^ b ] h ~ a b ( f ) 2 X − Y − Z = − 2 x sin x [ 2 r ^ 12 a r ^ 12 b − 2 r ^ 13 a r ^ 13 b − r ^ 23 a r ^ 23 b + r ^ 21 a r ^ 21 b − r ^ 31 a r ^ 31 b + r ^ 32 a r ^ 32 b ] h ~ a b ( f ) = − 2 x sin x 3 [ r ^ 12 a r ^ 12 b − r ^ 13 a r ^ 13 b ] h ~ a b ( f ) = 2 x sin x 3 3 2 [ x ^ a y ^ b + y ^ a x ^ b ] h ~ a b ( f ) \footnotesize
\begin{aligned}
X - Y &= - 2x\sin x \left[\hat{r}^a_{31}\hat{r}^b_{31} - \hat{r}^a_{32}\hat{r}^b_{32} - \hat{r}^a_{23}\hat{r}^b_{23} + \hat{r}^a_{21}\hat{r}^b_{21}\right] \tilde{h}_{ab}(f)\\
&= - 2x\sin x ~\frac{3}{2}~\left[\hat{y}^a\hat{y}^b - \hat{x}^a\hat{x}^b\right] \tilde{h}_{ab}(f)\\
2X - Y - Z &= - 2x\sin x \left[ 2\hat{r}^a_{12}\hat{r}^b_{12} - 2\hat{r}^a_{13}\hat{r}^b_{13} - \hat{r}^a_{23}\hat{r}^b_{23} + \hat{r}^a_{21}\hat{r}^b_{21}- \hat{r}^a_{31}\hat{r}^b_{31} + \hat{r}^a_{32}\hat{r}^b_{32}\right] \tilde{h}_{ab}(f)\\
&= - 2x\sin x ~3~\left[\hat{r}^a_{12}\hat{r}^b_{12} - \hat{r}^a_{13}\hat{r}^b_{13}\right] \tilde{h}_{ab}(f)
= 2x\sin x \frac{3\sqrt{3}}{2} \left[\hat{x}^a\hat{y}^b + \hat{y}^a\hat{x}^b\right] \tilde{h}_{ab}(f)\\
\end{aligned} X − Y 2 X − Y − Z = − 2 x sin x [ r ^ 3 1 a r ^ 3 1 b − r ^ 3 2 a r ^ 3 2 b − r ^ 2 3 a r ^ 2 3 b + r ^ 2 1 a r ^ 2 1 b ] h ~ a b ( f ) = − 2 x sin x 2 3 [ y ^ a y ^ b − x ^ a x ^ b ] h ~ a b ( f ) = − 2 x sin x [ 2 r ^ 1 2 a r ^ 1 2 b − 2 r ^ 1 3 a r ^ 1 3 b − r ^ 2 3 a r ^ 2 3 b + r ^ 2 1 a r ^ 2 1 b − r ^ 3 1 a r ^ 3 1 b + r ^ 3 2 a r ^ 3 2 b ] h ~ a b ( f ) = − 2 x sin x 3 [ r ^ 1 2 a r ^ 1 2 b − r ^ 1 3 a r ^ 1 3 b ] h ~ a b ( f ) = 2 x sin x 2 3 3 [ x ^ a y ^ b + y ^ a x ^ b ] h ~ a b ( f )
Z − Y 3 = 2 3 x sin x x ^ a x ^ b − y ^ a y ^ b 2 h ~ a b ( f ) 2 X − Y − Z 3 = 2 3 x sin x x ^ a y ^ b + y ^ a x ^ b 2 h ~ a b ( f ) S A = S E = 2 3 × 16 sin 2 x [ ( 1 + 1 2 cos x ) S O M S + 2 ( 1 + cos x + cos 2 x ) S a c c ] \begin{aligned}
\frac{Z - Y}{\sqrt{3}} &= 2\sqrt{3}~ x\sin x \frac{\hat{x}^a\hat{x}^b - \hat{y}^a\hat{y}^b}{2} \tilde{h}_{ab}(f)\\
\frac{2X - Y - Z}{3} &= 2\sqrt{3}~ x\sin x \frac{\hat{x}^a\hat{y}^b + \hat{y}^a\hat{x}^b}{2} \tilde{h}_{ab}(f) \\
S_A = S_E &= \frac{2}{3} \times 16\sin^2 x\left[(1+\frac{1}{2}\cos x)S_{\rm OMS} + 2(1+\cos x + \cos^2 x)S_{\rm acc}\right]
\end{aligned} 3 Z − Y 3 2 X − Y − Z S A = S E = 2 3 x sin x 2 x ^ a x ^ b − y ^ a y ^ b h ~ a b ( f ) = 2 3 x sin x 2 x ^ a y ^ b + y ^ a x ^ b h ~ a b ( f ) = 3 2 × 1 6 sin 2 x [ ( 1 + 2 1 cos x ) S O M S + 2 ( 1 + cos x + cos 2 x ) S a c c ]
Babak et al. 2021
X ~ 1.5 = 4 f f ∗ sin x 3 2 [ F + h ~ + + F × h ~ × ] \tilde{X}_{1.5} = 4 \frac{f}{f_*} \sin x \frac{\sqrt{3}}{2} [F_+\tilde{h}_+ + F_\times \tilde{h}_\times]
X ~ 1 . 5 = 4 f ∗ f sin x 2 3 [ F + h ~ + + F × h ~ × ]
变为应力响应（除以x x x 4 x 4x 4 x
X ~ 1.5 = sin x 3 2 [ F + h ~ + + F × h ~ × ] \tilde{X}_{1.5} = \sin x \frac{\sqrt{3}}{2} [F_+\tilde{h}_+ + F_\times \tilde{h}_\times]
X ~ 1 . 5 = sin x 2 3 [ F + h ~ + + F × h ~ × ]
S h , X 1.5 L W ( f ) = 10 3 S n , X 1.5 ( f ) 16 sin 2 x x 2 S^{LW}_{h,X_{1.5}} (f) = \frac{10}{3} \frac{S_{n,X_{1.5}}(f)}{16\sin^2x ~ x^2}
S h , X 1 . 5 L W ( f ) = 3 1 0 1 6 sin 2 x x 2 S n , X 1 . 5 ( f )
考虑到长波近似下X + Y + Z = 0 X + Y + Z=0 X + Y + Z = 0
A = 3 2 X , E = 1 2 ( X + 2 Y ) , T = 1 3 ( X + Y + Z ) A = \frac{\sqrt{3}}{2} X, ~~~~ E = \frac{1}{2}(X + 2Y), ~~~~ T = \frac{1}{3}(X + Y + Z)
A = 2 3 X , E = 2 1 ( X + 2 Y ) , T = 3 1 ( X + Y + Z )
[ 1 + exp ( − i ω 2 L / c ) ] [ 1 + exp ( i ω 2 L / c ) ] [1 + \exp (- i\omega ~ 2L/c)] [1+ \exp(i\omega ~ 2L/c)]
[ 1 + exp ( − i ω 2 L / c ) ] [ 1 + exp ( i ω 2 L / c ) ]
1 + exp ( i ω 2 L / c ) + exp ( − i ω 2 L / c ) + 1 1 + \exp (i\omega ~ 2L/c) + \exp (-i\omega ~ 2L/c) + 1
1 + exp ( i ω 2 L / c ) + exp ( − i ω 2 L / c ) + 1
2 + 2 cos ( ω 2 L / c ) 2 + 2 \cos(\omega ~ 2L/c)
2 + 2 cos ( ω 2 L / c )
因为TDI引入的e指数因子，ORF最终为虚数，计算信噪比时取模。
相位读出(采样)与插值
以上所有分析都是基于连续时间函数，默认任意时刻的数据都可直接得到，但实际数据是离散采样的。进行时延操作时，若延迟时间与采样率不匹配，就无法直接得到所需数据，需进行插值操作。
cos ϕ ( t ) \cos \phi(t) cos ϕ ( t ) ω ( t ) \omega(t) ω ( t ) ϕ ( t ) \phi(t) ϕ ( t )
在5MHz到25MHz波动的拍频下准确读出相位10 p m / H z 10 \rm pm/\sqrt{Hz} 1 0 p m / H z 1 p m / H z 1 \rm pm/\sqrt{Hz} 1 p m / H z
自适应激光锁频、激光噪声抑制、星间激光通信
激光不稳定性除了涉及相位/频率还涉及功率，被称为相对强度噪声，会耦合进光电探测器的散粒噪声，影响观测。目前的激光S R I N ∼ 1 0 − 4 H z \small \sqrt{S_{\rm RIN}} \sim 10^{-4} \sqrt{\rm Hz} S R I N ∼ 1 0 − 4 H z
激光的相对强度噪声、电子噪声也会影响光学测量读出噪声，低频抬升？
位移噪声：
光程噪声(optical pathlength noise)：光学平台位移、望远镜位移，(TTL噪声)
读出噪声(read out noise)：载波读出噪声、边带读出噪声
时钟噪声(clock noise)：使用导频信号抑制时钟噪声，同时会引入新噪声
读出：边带读出噪声
传输：导频传输路径上存在电子元件、电缆、光电调制(相位)、光纤、光纤放大等一些列噪声源
测量噪声(metrology system)：激光频率残余噪声(TDI之后)、相位计噪声
位移噪声在六路激光测量间相对独立，加速度噪声对于共享测试质量的连接臂是相关的
时钟噪声抑制需要将时钟信号调制到载波信号，消耗10%功率
数据处理技术
除了TDI激光频率噪声外，空间数据分析还有一些的不同于地面观测的问题。
白矮星前景扣除以及重叠信号的分离重构
数据异常处理
数据间断(gap)、非稳噪声(glitch)
混叠信号分离
白矮星前景扣除以及重叠信号的分离重构
Global Fit https://github.com/tlittenberg/ldasoft
LISA data analysis using MCMC methodshttps://www.ipam.ucla.edu/abstract/?tid=17067
GPU加速计算
Katz et al. 2020
