代数结构简介：群、环, 域、格、模...

Posted on 2018-05-21 In Learning , PhysMath Views: Waline:

群、环, 域、格、模、线性空间、域代数…本文内容对应于抽象代数，并没有学过这门课程，认知难免浅陋。

现在数学是建立在集合论这个共同的基础上的，集合论中有一些基本的概念，如集合、关系、函数、等价等，作为数学各个分支的共同语言，本文中数学概念的定义也都是从集合出发的。

数学结构

数学中，集合上的结构是指集合上附加的、赋予集合特殊含义的数学对象。常见的结构有序(Order)、代数结构、拓扑(Topology)、测度(Measure)、度量(Metric)/几何、等价关系、范畴(Category)、微分结构等。上世纪中期盛极一时的法国布尔巴基学派(结构主义)曾提出数学的三种基本结构：

代数结构：由集合及其上的运算组成，如群、环、域、模、线性空间等。
序结构：由集合及其上的序关系组成，如偏序集、全序集、良序集。
拓扑结构：由集合及其上的拓扑组成，如拓扑空间、度量空间、流形、紧致集等。

之后，随着代数拓扑学、微分拓扑学、代数几何学、李群和代数群理论、多复变量函数论、泛函分析等领域趋于平稳，而难以结构化的数学分支，如分析数学、概率论与统计学、离散数学(组合数学)、应用数学、计算数学等开始蓬勃发展，布尔巴基学派逐渐衰微。(p.s.感觉后面这些数学都大都更适于计算机处理，计算机的普及促进了新数学领域的发展。)

代数结构

抽象代数中，集合上的一个代数结构是指定义在集合上的一系列有限运算，而集合及其上的代数结构一起也被称为代数。常见的代数结构有群、环, 域、格、模、线性空间、域代数等。

群G(Group)：集合 + 一个二元运算(乘/加)
群是集合上定义了一个满足闭合性、结合律、单位元、可逆性(任何元素有逆元素)四条公理的二元运算的代数结构。注意上述公理中不包含交换律，交换律成立的群被称为阿贝尔群(交换群)。通常，群定义中的二元运算称为乘法，单位元写作1，此时群也被称为乘法群。对于满足交换律的阿贝尔群，二元运算通常称为加法，单位元写为0，因此阿贝尔群也被称为加法群。
可逆性意味着可以定义逆运算——除法，由于乘法不一定满足交换律，因此又可分为左除 $a^{-1}b(a\backslash b)$ $a−1b(a\b)$ 、右除 $ba^{-1}(b/a)$ $b a^{- 1} (b / a)$ 。对于满足交换律的阿贝尔群，两种除法相同，此时二元运算通常称为加法，逆运算称为减法。
- 半群：闭合于可结合二元运算下的集合形成的代数结构；相比群只要求二元运算满足闭合性和结合律，不需要有单位元和逆元。
- 幺半群(Monoid)：定义了可结合二元运算和单位元的代数结构，是带有单位元的半群；相比群不要求有逆元。
- 类似的代数结构还有：原群(Magma) > 拟群(Quasigroup, Loop) > 半群；半群胚 > 范畴(Category) > 群胚(Groupoid)
- 范畴不要求闭合性，但要求结合律和单位元，幺半群是特殊的范畴，只有一个对象(Object)。
环R(Ring)：集合 + 两个二元运算(乘、加)
环是集合上定义了满足特定公理的广义加法和乘法两个二元运算的代数结构。具体的：加法运算要满足结合律、交换律、单位元、可逆性四条公理；乘法运算要满足结合律；且乘法关于加法满足分配律。另一种说法是：环是一个关于加法的阿贝尔群；还是一个关于乘法的半群；且乘法关于加法满足分配律。
- 无零因子环：没有非0零因子的环称为无零因子环，0是唯一的零因子；等价的，也可以说是满足零乘性质的环：任何非0元素的乘积非0或If $ab=0$ , then $a=0$ or $b=0$ ；还可以说R\{0}对乘法封闭，构成一个半群。
- 幺环：如果环的乘法有单位元，则环是关于乘法的幺半群，环被称为幺环(维基中环的定义要求乘法有单位元)。
- 交换环(Commutative Ring)：环的加法满足交换律，但乘法不要求满足交换律；乘法满足交换律的环称为交换环。
- 除环/反称域(Division Ring/Skew Field)：环不要求乘法满足可逆性，乘法满足可逆性（所有非0元素存在逆元）的幺环称为除环。等价的可以说R\{0}对乘法形成一个群。除环不要求乘法的交换性，非交换的除环是体，交换的除环是域。
- 整环/整域(Entire Ring/Integral Domain)：无零因子的交换幺环；整环是整数环的推广，非零元素满足消去律：If $a≠0$ , $ab=ac$ implies $b=c$ 。
域F(Field)：性质良好的环
环中只对加法要求同时满足结合律、交换律、单位元、可逆性四条公理，乘法只需满足结合律。域则要求乘法也同时满足四条公理，唯一区别是乘法的可逆性仅针对非0元素。域关于加法也构成阿贝尔群，同时非0元素关于乘法构成阿贝群。域是交换的除环，是乘法可逆的整环。
域其实是大家最早接触的代数结构，如有理数域、实数域、复数域等各种“数”的域，事实上域就是数域的抽象推广。注意，对于整数集合，显然除法不满足可逆性，因此整数集合及加法、乘法构成整数环，而非整数域。数域也不仅限于上面常见的几个，如 $\{ a+b\sqrt{2}, a, b \in \mathbb{Q} \}$ 形式的实数关于加法、乘法也封闭为域，被称为有理数数域的扩域，记为 $\mathbb{Q}(\sqrt{2})$ 。而复数域可也视为实数域的扩域 $\{ a+b\sqrt{-1}, a, b \in \mathbb{R} \}$ 。有理数域是最小的数域，复数域是最大的数域。
另一个讨论较多的数域是代数数域：有理系数多项式的根被称为代数数，所有代数数关于加法和乘法构成代数数域。同时也存在非代数数，即不能表示为有理数多项式根的数，被称为超越数，如 $\pi, e$ 。显然代数数域不能包含实数域，但同时由于 $i$ 是代数数，因此实数域也不能包含代数数域。
注意，抽象代数中，中文域一般指Field，英文维基的环论下还有一个域(Domain)，没有对应的中文词条，是满足零乘性质的非零环，即非零的无零因子环。
线性空间(Linear Space)：域 + 阿贝尔群
线性空间也称向量空间(Vector Space)，不同于上面的群或环/域，其定义涉及了两个集合及相关运算。
- 一个标量的集合F，关于标量自身的加法和乘法构成“域”结构，其运算通常简称为域加法和域乘法；
- 一个向量的集合V，关于向量的加法构成“阿贝尔群”(交换群)，即向量加法满足结合律、交换律、单位元、可逆性；
- 两个集合由向量与标量的乘法连接，通常简称为标量乘法，标量乘法有单位元、与域乘法相容 $a(bα) = (ab)α$ ，且对向量加法及域加法满足分配律；
- 可将线性空间视为基于特定“域”定义的向量集合(Vector Space over a Field)，定义了向量加法和标量乘法两种运算。
模M(Module)：Vector Space over a Field $\rightarrow$ Module over a Ring 环 + 群
模是对线性空间概念的推广，线性空间中标量的代数结构是域(Field)，而模则将标量放宽到任意环(Ring)的元素，乘法运算定义在环元素与模元素之间。由于乘法不一定满足交换律，又可分为左L-模、右R-模。
域代数(Algebra over a Field)：线性空间再加上一个双线性运算(乘法)即成为域代数，如矩阵代数、张量代数、李代数、外代数。类似于线性空间推广到模，将标量的域F替换为交换环R，可以推广得到环代数(Algebra over a Ring)。
格L(Lattice)：集合 + 两个二元运算(交、并)
从序理论角度定义，格是一个偏序集，其非空有限子集都有一个上确界(并)和一个下确界(交)；从抽象代数角度定义，格是定义了满足交换律、结合律及吸收律三个公理的两个二元运算(交、并)的集合。

代数结构由集合上的满足特定公理的运算定义，而将这些代数结构本身作为研究对象的学科便是泛代数。范畴论是另一种研究代数结构间关系的工具：范畴是一系列对象及对象间箭头(态射)构成的代数结构；任意代数结构都有其同态的概念，从而可以构成一个范畴，比如所有的群及群同态便构成了群范畴。范畴论在编程语言理论中有重要应用，如函数式编程中单子的概念。

容纳运动是空间的本质特征，这里所说的运动是从一个点到另一个点的变换，而不是微积分意义上的“连续”性的运动。
认识到了这些，我们就可以把我们关于三维空间的认识扩展到其他的空间。事实上，不管是什么空间，都必须容纳和支持在其中发生的符合规则的运动（变换）。你会发现，在某种空间中往往会存在一种相对应的变换，比如拓扑空间中有拓扑变换，线性空间中有线性变换，仿射空间中有仿射变换，其实这些变换都只不过是对应空间中允许的运动形式而已。因此只要知道，“空间”是容纳运动的一个对象集合，而变换则规定了对应空间的运动。

代数空间
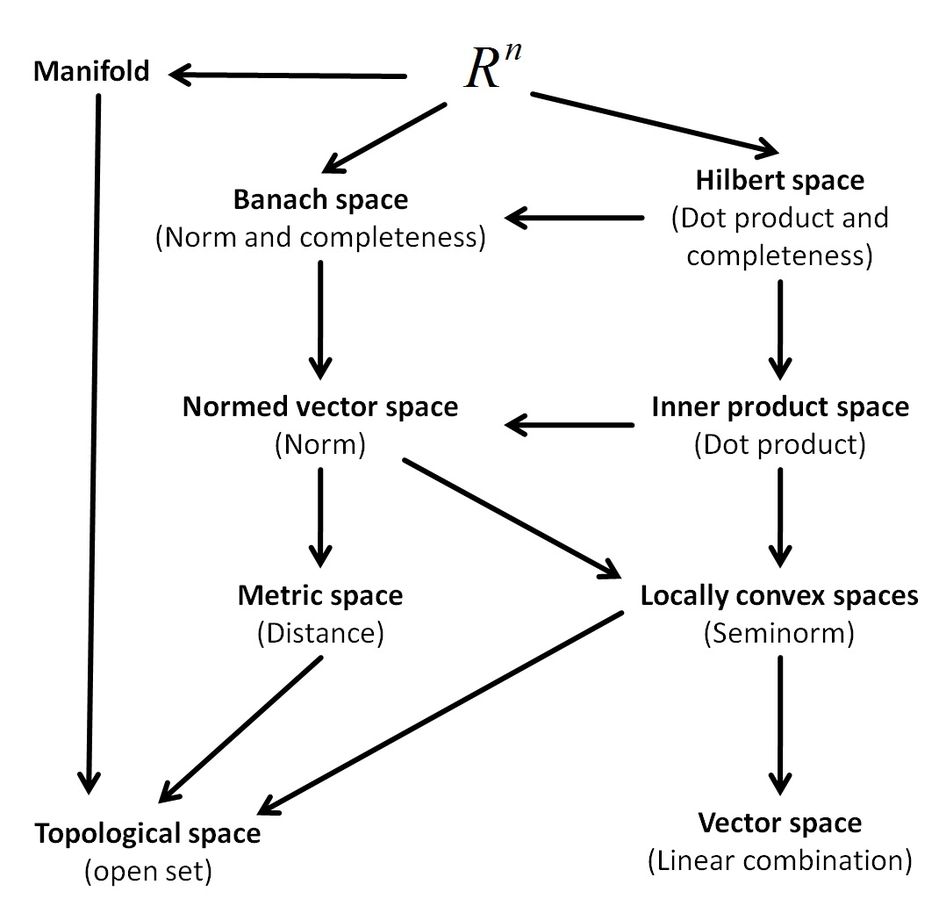
数学中，空间是指有额外(数学)结构的集合。常见的有线性空间(向量空间)、仿射空间、拓扑空间、测度空间、度量空间、赋范空间、内积空间、函数空间等。

度量空间是能在上面定义收敛, 连续概念的空间, 比度量空间更一般的空间是拓扑空间, 在拓扑空间上也能定义收敛和连续概念。
而测度空间是能在上面定义(Lebsegue)积分的空间。
赋范空间是线性空间中添加了距离的概念(范数)，而内积空间是线性空间添加了距离和角度两个概念(内积)。

测度空间与可测空间的区别, 可测空间是能在上面定义测度, 测度空间是已经在上面定义了测度。

希尔伯特空间
希尔伯特空间即完备的内积空间，也就是说一个带有内积的完备向量空间。当一个内积空间满足通过内积空间可推导出范数空间(赋范空间)，并且是完备的，那么这个内积空间就是希尔伯特空间。
如常见的 $\mathbb{R}^n$ ，满足内积运算，能够推导出 $l2$ 范数，且是完备的，所以是希尔伯特空间。

简单来说，基本的线性空间只包括加法和数乘操作，在此基础上我们引入内积操作，这样就把空间升级为内积空间。根据内积我们可以定义一个范数： $||x||=<x,x>$ 于是我们就得到了一个赋范向量空间。有了范数之后我们就可以引入一个度量： $d(x1,x2)=||x1-x2||$ 用于计算向量 $x1$ 和 $x2$ 之间的距离。于是我们就得到一个度量空间。如果这样的空间在这个度量下是完备的，那么这个空间叫做希尔伯特空间。