前面我们了解到比特(bit),也即二进制中的位,是信息的基本度量单位,本文针对这一点做进一步展开。本文受到 Loss Functions Explained By Siraj Raval 启发,主要参考了相关维基词条。
为方便理解,本文公式采用离散形式,但基本都可以无障碍的推广到积分形式
信息量
信息定量化的概念最早是由哈特莱 (Ralph Hartley) 于1928年提出,并选择了系统状态数(假设各状态等概率)的对数作为信息的度量。20年后,1948年信息论奠基人香农 (Claude E. Shannon) ,在其划时代的论文 A mathematical theory of communication 中详细讨论了这一问题:
…the actual message is one selected from a set of possible messages. …If the number of messages in the set is finite then this number or any monotonic function of this number can be regarded as a measure of the information produced when one message is chosen from the set, all choices being equally likely. As was pointed out by Hartley the most natural choice is the logarithmic function.
The choice of a logarithmic base corresponds to the choice of a unit for measuring information. If the base 2 is used the resulting units may be called binary digits, or more briefly bits, a word suggested by J. W. Tukey. …
香农在论文中指出,对数底数的选择对应于信息度量单位的选择 ,并将以2为底数时对应的信息量单位称为比特 (binary digits, bit) ,与二进制系统的信息存储相对应;而以10为底情况称为decimal digits (dit, ban,也被称为Hartley) ;以e为底情况称为natural units(nat)。不同单位间根据对数的性质,相差一个常数倍(换底公式)。
香农认为信息的基本作用是消除人们对事物认知的不确定性。因此能够降低系统不确定性的才是有效信息,其余的则属于冗余信息。有效信息量的大小由信息消除不确定性的程度决定:1比特的信息量对应于系统的不确定性减半。
以前段的世界杯为例,某场球赛双方实力均等,胜率都是50 % 50\% 5 0 % 2 3 = 8 , log 2 8 = 3 2^3=8, \log_2 8=3 2 3 = 8 , log 2 8 = 3
从上面可以看出,有效信息量就等于系统不确定性降低程度的二进制对数(以2为底的对数)。比如某个随机事件发生的概率为p ( x ) p(x) p ( x ) 1 / p ( x ) 1/p(x) 1 / p ( x ) I ( x ) = log 2 1 p ( x ) = − log 2 p ( x ) bit \textcolor{blue}{I(x) = \log_2 \frac{1}{p(x)} = -\log_2 p(x)\textrm{bit}} I ( x ) = l o g 2 p ( x ) 1 = − l o g 2 p ( x ) bit
回到前面的例子:对于两只球队情况,一只球队获胜概率为1 / 2 1/2 1 / 2 log 2 2 = 1 \log_2 2=1 log 2 2 = 1 1 / 8 1/8 1 / 8 log 2 8 = 3 \log_2 8=3 log 2 8 = 3 25 % 25\% 2 5 % − log 2 0.25 = 2 -\log_2 0.25 = 2 − log 2 0 . 2 5 = 2 − log 2 0.75 = 0.415 -\log_2 0.75 = 0.415 − log 2 0 . 7 5 = 0 . 4 1 5
最后,我们再来看一个经典的编码问题——老鼠毒药问题:
1000瓶无色液体中有一瓶毒药,其余为清水,老鼠吃到毒药一天内会死,现要求在一天内检测出有毒药瓶,至少需要几只老鼠?
乍一看可能以为这是一个抽样问题,但其实问题跟概率完全没关系。要用尽量少的老鼠,又限制检测时间为毒发时间,肯定要将液体混着喂,但要怎么混使用老鼠才最少,这其实是个编码问题。我们将问题换个说法就清晰了:1000个不同的状态用二进制编码需要几位?一天后老鼠的状态有生、死两种,因此是二进制编码。
不考虑实际操作,仅从信息编码角度考虑,1000个状态最少需要10位二进制来编码。具体操作:根据瓶子编码,如1001001010,将所有第一位为1的瓶子液体取少量混合喂给第一只老鼠,依次类推,最后根据第二天老鼠生死状态判断有毒瓶子的编码中那几位为1。1 1000 \frac{1}{1000} 1 0 0 0 1 log 2 1000 = 9.97 \log_2 1000=9.97 log 2 1 0 0 0 = 9 . 9 7 C 1000 2 C_{1000}^2 C 1 0 0 0 2 2 1000 × 1 999 \frac{2}{1000}\times \frac{1}{999} 1 0 0 0 2 × 9 9 9 1 log 2 ( 500 × 999 ) = 18.93 \log_2 (500\times 999)=18.93 log 2 ( 5 0 0 × 9 9 9 ) = 1 8 . 9 3
接下来,问题再复杂点:还是一瓶毒药,要求在两天内检测出有毒药瓶,至少需要几只老鼠?log 2 500 = 8.97 \log_2 500=8.97 log 2 5 0 0 = 8 . 9 7 log 3 1000 = 6.29 \log_3 1000=6.29 log 3 1 0 0 0 = 6 . 2 9 log 2 1000 \log_2 1000 log 2 1 0 0 0 log 2 3 \log_2 3 log 2 3 l o g 2 1000 log 2 3 = log 3 1000 = 6.29 \frac{log_2 1000}{\log_2 3}= \log_3 1000=6.29 l o g 2 3 l o g 2 1 0 0 0 = log 3 1 0 0 0 = 6 . 2 9
具体要如何操作呢?稍微有点复杂,但基本思路与之前相同:
第一天,取所有三进制编码第一位是2的瓶子液体少许,混合后喂给第一只老鼠,依次类推;
第一天结束,根据老鼠生死状态判断有毒瓶子编码中哪几位为2(死老鼠对应的位),这些位上编码不是2的瓶子直接筛除;
对于其余位,对应的老鼠都没死。在第二天,取这些位中编码是1的瓶子液体取少量,混合后喂给相应位对应的老鼠;
第二天结束,根据老鼠状态判断有毒瓶子编码中哪几位为1,并最终确定毒药瓶三进制编码。
不借助信息编码视角,应该很难想到这一“最优”方案。
关于信息编码还有一个经典的称球问题 :N N N 一定 能找出次品球?或者反过来:用天平称k k k 这篇文章 ,这里直接给出结论(⌈⌉为向上取整,⌊⌋为向下取整):
已知次品球偏轻(重):最少称重次数⌈ log 3 N ⌉ \lceil\log_3 N\rceil ⌈ log 3 N ⌉ 3 k 3^k 3 k
不知次品球重量偏向:最少称重次数⌈ log 3 2 N ⌉ \lceil\log_3 2N\rceil ⌈ log 3 2 N ⌉ ⌊ 3 k 2 ⌋ = 3 k − 1 2 \displaystyle\lfloor\frac{3^k}{2}\rfloor=\frac{3^k-1}{2} ⌊ 2 3 k ⌋ = 2 3 k − 1
找出次品球重量偏向:最少称重次数⌈ log 3 2 ( N + 1 ) ⌉ \lceil\log_3 2(N+1)\rceil ⌈ log 3 2 ( N + 1 ) ⌉ ⌊ 3 k 2 ⌋ − 1 = 3 k − 3 2 \displaystyle\lfloor\frac{3^k}{2}\rfloor-1=\frac{3^k-3}{2} ⌊ 2 3 k ⌋ − 1 = 2 3 k − 3 注:后两种情况的公式跟维基不一致,虽然不影响取整后结果,但本质上的信息量是不同的,我还没想清信息量到底是多少😖,存疑。
N N N
信息熵
从前面两只球队的例子可以看到,当两队胜率不一样时,每只球队获胜所包含的信息量(不确定性的降低程度)是不一样的。那么我们随机获得一个比赛结果(抽取一个样本),系统不确定性降低程度的期望,或者说我们能获得信息量的期望应为0.25 × 2 + 0.75 × 0.415 = 0.81 0.25 \times 2 + 0.75 \times 0.415 = 0.81 0 . 2 5 × 2 + 0 . 7 5 × 0 . 4 1 5 = 0 . 8 1
香农将这一期望值称为系统的信息熵(Entropy) ,用以表征随机抽取一个样本所预期获得的信息量:
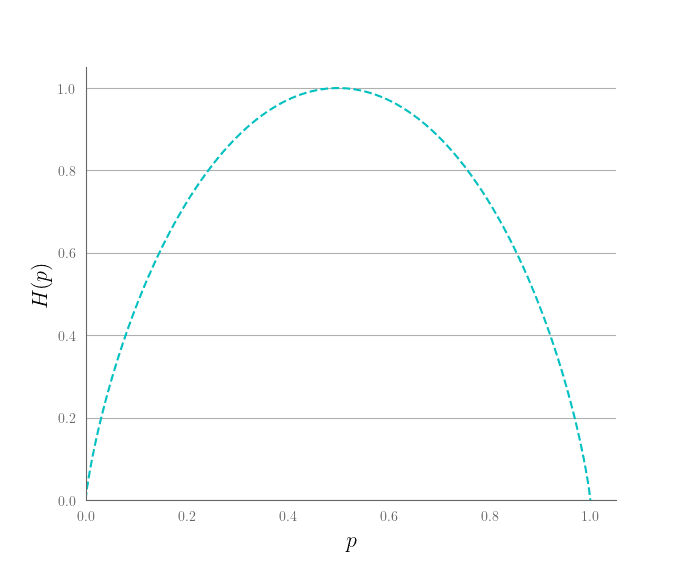
H ( p ) = − ∑ i p i log 2 p i = E { − log 2 p } H(p) = -\sum_{i} p_i \log_2~p_i = \mathbb{E}\{-\log_2 p\}
H ( p ) = − i ∑ p i log 2 p i = E { − log 2 p }
其中符号H H H H定理 (本质上就是统计物理中的熵):
The form of H H H p i p_i p i i i i H H H H H H H H H
作为对比,统计物理中的熵(Entropy) :
Clausius Entropy: d S = ( d Q T ) 可逆过程 Boltzmann Entropy: S = k B ln Ω Gibbs Entropy: S = − k B ∑ i p i ln p i \begin{aligned}
\text{Clausius Entropy:}~~~ dS &= \left(\frac{dQ}{T}\right)_{\text{可逆过程}} \\
\text{Boltzmann Entropy:}~~~ S &= k_B\ln\Omega\\
\text{Gibbs Entropy:}~~~ S &= -k_B\sum_{i} p_i \ln~p_i
\end{aligned} Clausius Entropy: d S Boltzmann Entropy: S Gibbs Entropy: S = ( T d Q ) 可逆过程 = k B ln Ω = − k B i ∑ p i ln p i
其中k B k_B k B Ω \Omega Ω p i p_i p i i i i equal a priori probability postulate : 对于给定能量和组分的孤立系统,没有其他信息情况下,系统处于各微观状态的概率均等),便可由吉布斯熵得到玻尔兹曼熵。
通过研究卡诺热机,克劳修斯于1850年首次明确指出热力学第二定律(熵增定律)的基本概念,并于1865年引入了熵的概念,作为描述系统“能量退化”的状态参数。此时熵作为一个宏观观测量,其本质尚不清楚。玻尔兹曼在1866年开始使用ρ l n ρ \textcolor{orange}{\rho ln \rho} ρ l n ρ ρ \rho ρ [wiki]
信息熵与物理熵的关系 Information is Physical 这个赌徒,连接了物质与信息 How Quantum Entanglement Creates Entropy
1867年,麦克斯韦针对热力学第二定律,提出了著名的思想实验麦克斯韦妖 。
直到香农建立信息熵之后,Landauer于1960年k T ln 2 kT \ln 2 k T ln 2
2011年,物理学学家发现,虽然信息擦除必定增加熵,但却不一定消耗能量,而可以消耗其他守恒量,如角动量;2012年,物理学家测到了擦除1bit数据时所产生的热量。
https://www.youtube.com/watch?v=KR23aMjIHIY
1982年,Bennett
In 1960, Rolf Landauer raised an exception to this argument.
Landauer’s principle demonstrates the reality of this by stating the minimum energy E required (and therefore heat Q generated) by an ideally efficient memory change or logic operation by irreversibly erasing or merging N h bits of information will be S times the temperature which is
E = Q = T k B ln ( 2 ) N h {\displaystyle E=Q=Tk_{\mathrm {B} }\ln(2)Nh} {\displaystyle E=Q=Tk_{\mathrm {B} }\ln(2)Nh}
where h is in informational bits and E and Q are in physical Joules. This has been experimentally confirmed.[
One of information thermodynamics’ most important theoretical insights, drawing on 1950s work by John von Neumann and proposed by Rolf Landauer in 1961, is that there’s an absolute energy cost to irreversibly changing any bit of information, something that you can never beat. That so-called Landauer limit is thanks to entropy (and the fact that organized change pushes again a universal tendency for disorder), and depends solely on the temperature at which the information change takes place.
Remarkably it seems that biology also adheres to that limit, and can operate very, very close to it. In 2017 the biologist and complexity scientist Chris Kempes and his colleagues pointed out that when the process of RNA translation takes an amino acid and attaches it to a chain of other amino acids (making or “computing” a protein inside cells) the energy involved is within a factor of 10 of the Landauer limit—which is an absolutely tiny 10-20 joules at room temperature.
https://www.scientificamerican.com/article/to-find-life-in-the-universe-find-the-computation/ https://plato.stanford.edu/entries/information-entropy/ https://royalsocietypublishing.org/doi/full/10.1098/rsta.2016.0343
信息熵度量了我们能够从一个随机系统的样本中所能获得的平均信息量(期望);也表征了一个随机系统不可预测的程度:系统随机性越大,越混乱,信息熵就越大。前面的信息量反映的是一个具体事件发生所带来的信息;而信息熵表示的则是在结果出来之前,对于所能获得信息量的预期,即信息量的期望值。信息熵有以下性质:
信息熵非负,且只有当系统没有不确定性时才为0;
log \log log H ( x ) = E log 2 1 p ( x ) ≤ log 2 E 1 p ( x ) = log 2 n H(x) = \mathbb{E}\log_2 \frac{1}{p(x)} \le \log_2 \mathbb{E}\frac{1}{p(x)} = \log_2 n H ( x ) = E log 2 p ( x ) 1 ≤ log 2 E p ( x ) 1 = log 2 n n n n log 2 n \log_2 n log 2 n 联合熵 H ( x , y ) ≤ H ( x ) + H ( y ) H(x,y) \le H(x) + H(y) H ( x , y ) ≤ H ( x ) + H ( y ) X X X Y Y Y X X X Y Y Y X X X Y Y Y 条件熵 H ( y ∣ x ) = 0 H(y∣x)=0 H ( y ∣ x ) = 0 Y Y Y X X X p ( y ∣ x ) p(y∣x) p ( y ∣ x ) H ( x , y ) = H ( x ) + H ( y ∣ x ) = H ( y ) + H ( x ∣ y ) H(x,y) = H(x) + H(y|x) = H(y) + H(x|y) H ( x , y ) = H ( x ) + H ( y ∣ x ) = H ( y ) + H ( x ∣ y ) X X X Y Y Y X X X X X X Y Y Y 结合前者有H ( y ∣ x ) ≤ H ( y ) H(y|x) \le H(y) H ( y ∣ x ) ≤ H ( y ) X X X Y Y Y
H ( y ∣ x ) = H ( x ∣ y ) + H ( y ) − H ( x ) H(y|x) = H(x|y) + H(y) - H(x) H ( y ∣ x ) = H ( x ∣ y ) + H ( y ) − H ( x ) 贝叶斯公式的信息熵表达;∀ f , H ( f ( x ) ∣ x ) = 0 , H ( x ∣ f ( x ) ) ≥ 0 \forall f, H(f(x)|x) =0 , H(x|f(x)) \ge 0 ∀ f , H ( f ( x ) ∣ x ) = 0 , H ( x ∣ f ( x ) ) ≥ 0 H ( f ( x ) ) ≤ H ( x ) H(f(x)) \le H(x) H ( f ( x ) ) ≤ H ( x )
最后,我们回到两只球队的例子:不确定性最大(最随机)的情况便是两队胜率均等,此时系统信息熵为 0.5 × 1 + 0.5 × 1 = 1 0.5\times 1 + 0.5\times 1 = 1 0 . 5 × 1 + 0 . 5 × 1 = 1
联合熵 (Joint Entropy),即联合分布p ( x , y ) p(x,y) p ( x , y )
H ( x , y ) = − ∑ x , y p ( x , y ) log 2 p ( x , y ) H(x,y) = -\sum_{x,y} p(x,y) \log_2~p(x,y)
H ( x , y ) = − x , y ∑ p ( x , y ) log 2 p ( x , y )
条件熵 (Conditional Entropy),即条件概率p ( y ∣ x ) p(y|x) p ( y ∣ x )
H ( y ∣ x ) = − ∑ x p ( x ) ∑ y p ( y ∣ x ) log 2 p ( y ∣ x ) = − ∑ x , y p ( x , y ) log 2 p ( y ∣ x ) = ∑ x , y p ( x , y ) log 2 p ( x ) p ( x , y ) \begin{aligned}
H(y|x) &= -\sum_{x} p(x) \sum_{y} p(y|x) \log_2~p(y|x)\\
&= -\sum_{x,y} p(x,y) \log_2~p(y|x)\\
&= \sum_{x,y} p(x,y) \log_2~\frac{p(x)}{p(x,y)}
\end{aligned}
H ( y ∣ x ) = − x ∑ p ( x ) y ∑ p ( y ∣ x ) log 2 p ( y ∣ x ) = − x , y ∑ p ( x , y ) log 2 p ( y ∣ x ) = x , y ∑ p ( x , y ) log 2 p ( x , y ) p ( x )
互信息 (Mutual Information):
I ( x ; y ) = ∑ x , y p ( x , y ) log 2 p ( x , y ) p ( x ) p ( y ) I(x;y) = \sum_{x,y} p(x,y) \log_2~\frac{p(x,y)}{p(x)p(y)}
I ( x ; y ) = x , y ∑ p ( x , y ) log 2 p ( x ) p ( y ) p ( x , y )
由Jensen不等式,I ( x ; y ) ≥ 0 I(x;y) \ge 0 I ( x ; y ) ≥ 0 I ( x ; y ) = 0 I(x;y)=0 I ( x ; y ) = 0 X X X Y Y Y I ( x ; y ) = I ( y ; x ) I(x;y)=I(y;x) I ( x ; y ) = I ( y ; x ) I ( x ; y ) ≤ H ( X ) , I ( x ; y ) ≤ H ( y ) I(x;y) \le H(X), I(x;y) \le H(y) I ( x ; y ) ≤ H ( X ) , I ( x ; y ) ≤ H ( y ) X X X Y Y Y H ( x ) , H ( y ) , H ( x ∣ y ) , H ( y ∣ x ) , H ( x , y ) H(x), H(y), H(x|y), H(y|x), H(x,y) H ( x ) , H ( y ) , H ( x ∣ y ) , H ( y ∣ x ) , H ( x , y )
I ( x ; y ) = H ( x ) − H ( x ∣ y ) = H ( y ) − H ( y ∣ x ) = H ( x ) + H ( y ) − H ( x , y ) = H ( x , y ) − H ( x ∣ y ) − H ( y ∣ x ) \begin{aligned}
I(x;y) &= H(x) - H(x|y)\\
&= H(y) - H(y|x)\\
&= H(x) + H(y) - H(x,y)\\
&= H(x,y) - H(x|y) - H(y|x)\\
\end{aligned}
I ( x ; y ) = H ( x ) − H ( x ∣ y ) = H ( y ) − H ( y ∣ x ) = H ( x ) + H ( y ) − H ( x , y ) = H ( x , y ) − H ( x ∣ y ) − H ( y ∣ x )
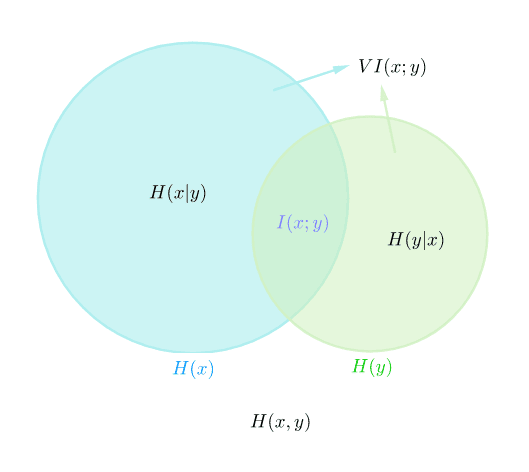
由互信息可引出一种随机变量相似度的距离度量(variation of information):
V I ( x ; y ) = H ( x ∣ y ) + H ( y ∣ x ) = H ( x , y ) − I ( x ; y ) = H ( x ) + H ( y ) − 2 I ( x ; y ) \begin{aligned}
VI(x;y) &= H(x|y) + H(y|x)\\
&= H(x,y) - I(x;y)\\
&= H(x) + H(y) - 2I(x;y)
\end{aligned}
V I ( x ; y ) = H ( x ∣ y ) + H ( y ∣ x ) = H ( x , y ) − I ( x ; y ) = H ( x ) + H ( y ) − 2 I ( x ; y )
统计距离
由信息熵可自然引出几个度量随机分布相似度的统计量,即所谓的统计距离( Statistical Distance ),比如上面提到的V I ( x ; y ) VI(x;y) V I ( x ; y )
对称d ( x , y ) = d ( y , x ) d(x,y)=d(y,x) d ( x , y ) = d ( y , x )
非负d ( x , y ) ≥ 0 d(x,y) \ge 0 d ( x , y ) ≥ 0 x = y x=y x = y
满足三角不等式d ( x , z ) ≤ d ( x , y ) + d ( y , z ) d(x,z) \le d(x,y)+d(y,z) d ( x , z ) ≤ d ( x , y ) + d ( y , z )
其中非负是最基本的要求,但对称性及三角不等式,统计学中的距离度量却不一定满足,因此并不是严格意义上的Metric (距离):两者都不满足的一般称为Divergence (散度);满足对称性但不满足三角不等式的则会被称为Distance (距离);但又有一些两者都满足的也会被称为Distance ,有点乱。p.s. 反正汉语也没法区分😋
统计距离通常用于概率密度(分布)函数,但也有用于样本的情况,注意符号上的区别:
p i p_i p i i i i 概率;x i x_i x i i i i 样本p i p_i p i x i x_i x i
本文讨论的统计距离大部分都是应用于概率分布的,因此出现的都是p i p_i p i p ( x ) p(x) p ( x )
交叉熵(Cross Entropy)
H ( p , q ) = − ∑ i p i ln q i = E p [ − ln q ] H(p,\textcolor{blue}{q}) = -\sum_{i} p_i \ln \textcolor{blue}{q_i} = \mathbb{E}_p [-\ln \textcolor{blue}{q}]
H ( p , q ) = − i ∑ p i ln q i = E p [ − ln q ]
交叉熵用来衡量在给定的真实分布下,使用非真实分布所指定的策略消除系统的不确定性所需要付出的努力的大小。
实例:由极大似然估计可以得到Logistic回归的损失函数为交叉熵H ( y , y ^ ) H(y,\hat y) H ( y , y ^ ) y y y y ^ = sigmoid ( θ T x + b ) = p ( y = 1 ∣ x ) \hat y = \operatorname{sigmoid}(\theta^Tx+b) = p(y=1|x) y ^ = s i g m o i d ( θ T x + b ) = p ( y = 1 ∣ x )
吉布斯不等式 :H ( p , q ) ≥ H ( p ) H(p,q) \ge H(p) H ( p , q ) ≥ H ( p ) p p p q q q
相对熵(Relative Entropy)常被称为K-L 散度(Kullback–Leibler Divergence)或信息增益(Information Gain),其形式为:
H ( p ∣ ∣ q ) = − ∑ i p i ln ( q i p i ) = E p [ ln p − ln q ] = H ( p , q ) − H ( p ) H(p||q) =-\sum_{i} p_i \ln \left(\frac{q_i}{p_i}\right) = \mathbb{E}_p[\ln p - \ln q] = H(p,q) - H(p)
H ( p ∣ ∣ q ) = − i ∑ p i ln ( p i q i ) = E p [ ln p − ln q ] = H ( p , q ) − H ( p )
或公式推导时更常见的积分形式(连续型随机变量):
H ( p ∣ ∣ q ) = − ∫ p ( x ) ln q ( x ) p ( x ) d x = ∫ p ( x ) ln p ( x ) q ( x ) d x H(p||q) = -\int p(x) \ln\frac{q(x)}{p(x)} dx= \int p(x) \ln\frac{p(x)}{q(x)} dx
H ( p ∣ ∣ q ) = − ∫ p ( x ) ln p ( x ) q ( x ) d x = ∫ p ( x ) ln q ( x ) p ( x ) d x
由Jensen不等式可以证明K-L 散度非负:− ln -\ln − ln
E p [ − ln q p ] ≥ − ln E p [ q p ] = − ln 1 = 0 \mathbb{E}_p\left[-\ln\frac{q}{p}\right] \ge -\ln \mathbb{E}_p\left[\frac{q}{p}\right] = -\ln1 = 0
E p [ − ln p q ] ≥ − ln E p [ p q ] = − ln 1 = 0
由于K-L 散度非负,且H ( p ∣ ∣ q ) = 0 ⟺ q = p H(p||q)=0 \iff q=p H ( p ∣ ∣ q ) = 0 ⟺ q = p D K L ( p ∣ ∣ q ) D_{KL}(p||q) D K L ( p ∣ ∣ q ) D K L ( p ∣ ∣ q ) ≠ D K L ( q ∣ ∣ p ) D_{KL}(p||q) \neq D_{KL}(q||p) D K L ( p ∣ ∣ q ) = D K L ( q ∣ ∣ p )
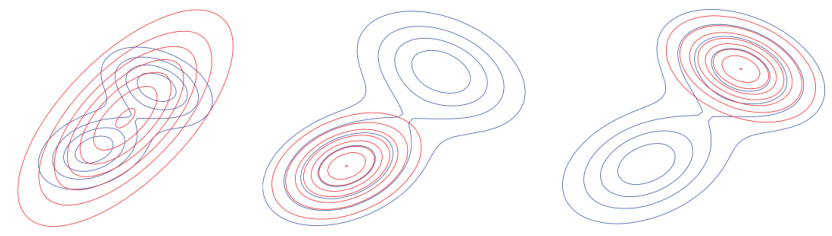
在贝叶斯推断领域,D K L ( p ∣ ∣ q ) D_{KL}(p||q) D K L ( p ∣ ∣ q ) q ( x ) q(x) q ( x ) p ( x ) p(x) p ( x ) D K L ( p ∣ ∣ q ) D_{KL}(p||q) D K L ( p ∣ ∣ q ) q ( x ) q(x) q ( x ) p ( x ) p(x) p ( x ) p ( x ) p(x) p ( x ) q ( x ) q(x) q ( x ) q ( x ) q(x) q ( x ) p ( x ) p(x) p ( x ) K-L 散度可以得到最接近真实分布/最符合观测数据的近似分布/理论模型。但由于K-L 散度的非对称性,D K L ( p ∣ ∣ q ) D_{KL}(p||q) D K L ( p ∣ ∣ q ) D K L ( q ∣ ∣ p ) D_{KL}(q||p) D K L ( q ∣ ∣ p )
最小化D K L ( p ∣ ∣ q ) D_{KL}(p||q) D K L ( p ∣ ∣ q ) p ( x ) p(x) p ( x ) q ( x ) q(x) q ( x ) p ( x ) q ( x ) \frac{p(x)}{q(x)} q ( x ) p ( x )
最小化D K L ( q ∣ ∣ p ) D_{KL}(q||p) D K L ( q ∣ ∣ p ) p ( x ) p(x) p ( x ) q ( x ) q(x) q ( x ) q ( x ) p ( x ) \frac{q(x)}{p(x)} p ( x ) q ( x )
两者是一致的,但效果却不完全相同,比如用高斯分布q ( x ) q(x) q ( x ) p ( x ) p(x) p ( x )
最后,D K L ( p ∣ ∣ q ) D_{KL}(p||q) D K L ( p ∣ ∣ q )
为了克服相对熵作为“距离”的缺点,人们又引入了JS 散度,用于生成对抗网络(GAN)。
JS 散度(Jensen–Shannon Divergence):
D J S ( p ∣ ∣ q ) = 1 2 [ D K L ( p ∣ ∣ m ) + D K L ( q ∣ ∣ m ) ] , m = 1 2 ( p + q ) D_{JS}(p||q) = \frac{1}{2}[D_{KL}(p||m) + D_{KL}(q||m)], m=\frac{1}{2}(p+q)
D J S ( p ∣ ∣ q ) = 2 1 [ D K L ( p ∣ ∣ m ) + D K L ( q ∣ ∣ m ) ] , m = 2 1 ( p + q )
如果两个分配P,Q离得很远,完全没有重叠的时候,那么KL散度值是没有意义的,而JS散度值是一个常数。这在学习算法中是比较致命的,这就意味这这一点的梯度为0。梯度消失了。
K-L 散度其实是更一般的f f f f f f
D f ( p ∣ ∣ q ) = ∫ q ( x ) f ( p ( x ) q ( x ) ) d x D_f(p||q) = \int q(x)f\left(\frac{p(x)}{q(x)}\right) dx
D f ( p ∣ ∣ q ) = ∫ q ( x ) f ( q ( x ) p ( x ) ) d x
其中函数f \bm{f} f p ( x ) q ( x ) \bm{\frac{p(x)}{q(x)}} q ( x ) p ( x ) f ( 1 ) = 0 \bm{f(1)=0} f ( 1 ) = 0 。由Jensen不等式,E [ f ( t ) ] ≥ f ( E [ t ] ) \mathbb{E}[f(t)] \ge f(\mathbb{E}[t]) E [ f ( t ) ] ≥ f ( E [ t ] )
D f ( p ∣ ∣ q ) = ∫ q ( x ) f ( p ( x ) q ( x ) ) d x ≥ f ( ∫ q ( x ) p ( x ) q ( x ) ) d x = f ( 1 ) = 0 D_f(p||q) = \int q(x)f\left(\frac{p(x)}{q(x)}\right) dx \ge f\left(\int q(x) \frac{p(x)}{q(x)}\right) dx = f(1) = 0
D f ( p ∣ ∣ q ) = ∫ q ( x ) f ( q ( x ) p ( x ) ) d x ≥ f ( ∫ q ( x ) q ( x ) p ( x ) ) d x = f ( 1 ) = 0
即f f f p = q p=q p = q f f f f f f
名称
f ( t ) f(t) f ( t ) 具体形式
K-L 散度t log t t~\log t t log t D K L ( p ∣ q ) = ∫ p ( x ) ln p ( x ) q ( x ) d x D_{KL}(p|q) = \displaystyle\int p(x) \ln\frac{p(x)}{q(x)} dx D K L ( p ∣ q ) = ∫ p ( x ) ln q ( x ) p ( x ) d x
总变差距离
1 2 ∣ t − 1 ∣ \frac{1}{2} \vert t-1\vert 2 1 ∣ t − 1 ∣ δ ( p , q ) = 1 2 ∫ ∣ p ( x ) − q ( x ) ∣ d x \delta(p,q) = \displaystyle\frac{1}{2} \displaystyle\int \vert p(x)-q(x)\vert dx δ ( p , q ) = 2 1 ∫ ∣ p ( x ) − q ( x ) ∣ d x
χ 2 \chi^2 χ 2 ( t − 1 ) 2 , t 2 − 1 (t-1)^2,~ t^2-1 ( t − 1 ) 2 , t 2 − 1 χ 2 ( p ∣ q ) = ∫ ( p ( x ) − q ( x ) ) 2 q ( x ) d x \chi^2(p|q) = \displaystyle\int \frac{(p(x)-q(x))^2}{q(x)} dx χ 2 ( p ∣ q ) = ∫ q ( x ) ( p ( x ) − q ( x ) ) 2 d x
Hellinger距离
1 2 ( t − 1 ) 2 , 1 − t \frac{1}{2} (\sqrt{t}-1)^2,~ 1-\sqrt{t} 2 1 ( t − 1 ) 2 , 1 − t H 2 ( p , q ) = 1 2 ∫ ( p ( x ) − q ( x ) ) 2 d x H^2(p,q) = \displaystyle\frac{1}{2} \int\left(\sqrt{p(x)}-\sqrt{q(x)}\right)^2 dx H 2 ( p , q ) = 2 1 ∫ ( p ( x ) − q ( x ) ) 2 d x
其中K-L 散度及χ 2 \chi^2 χ 2
总变差距离(Total Variation Distance)/the Statistical Distance σ \sigma σ δ ( p , q ) = sup A ∈ F ∣ p ( A ) − q ( A ) ∣ , sup \delta(p,q)=\displaystyle\sup_{A\in \mathcal{F}}|p(A)-q(A)|, \sup δ ( p , q ) = A ∈ F sup ∣ p ( A ) − q ( A ) ∣ , sup
δ ( p , q ) = 1 2 ∑ i ∣ p i − q i ∣ = 1 2 ∣ ∣ p − q ∣ ∣ \delta(p,q) = \frac{1}{2}\sum_i |p_i-q_i| =\frac{1}{2}||p-q||
δ ( p , q ) = 2 1 i ∑ ∣ p i − q i ∣ = 2 1 ∣ ∣ p − q ∣ ∣
Pinsker不等式 δ ( p , q ) ≤ 1 2 D K L ( p ∣ ∣ q ) , ∣ ∣ p ( x ) , q ( x ) ∣ ∣ ≤ 2 D K L ( p ∣ ∣ q ) \textrm{\small Pinsker不等式}~~~\delta(p,q) \le \sqrt{\frac{1}{2} D_{KL}(p||q)},~||p(x),q(x)|| \le \sqrt{2 D_{KL}(p||q)}
Pinsker 不等式 δ ( p , q ) ≤ 2 1 D K L ( p ∣ ∣ q ) , ∣ ∣ p ( x ) , q ( x ) ∣ ∣ ≤ 2 D K L ( p ∣ ∣ q )
~~~~~~~~~~~~~~ D K L ( p ∣ ∣ q ) D_{KL}(p||q) D K L ( p ∣ ∣ q )
χ 2 \chi^2 χ 2
χ 2 = N ∑ i n ( p i − q i ) 2 q i \chi^2 = N \sum_i^n\frac{(p_i-q_i)^2}{q_i}
χ 2 = N i ∑ n q i ( p i − q i ) 2
其中N N N n n n p p p χ 2 \chi^2 χ 2 n − p n-p n − p
χ 2 \chi^2 χ 2
约化的χ 2 \chi^2 χ 2
海林格距离(Hellinger Distance)
H 2 ( p , q ) = 1 2 ∑ i ( p i − q i ) 2 = 1 − ∑ i p i q i H^2(p,q) = \frac{1}{2}\sum_{i}\left(\sqrt{p_i} - \sqrt{q_i}\right)^2 = 1 - \sum_i \sqrt{p_iq_i}
H 2 ( p , q ) = 2 1 i ∑ ( p i − q i ) 2 = 1 − i ∑ p i q i
∑ i p i q i ≥ 0 \sum_i \sqrt{p_iq_i} \ge 0 ∑ i p i q i ≥ 0 H 2 ( p , q ) ≤ 1 H^2(p,q) \le 1 H 2 ( p , q ) ≤ 1 f f f 0 ≤ H 2 ( p , q ) ≤ 1 0 \le H^2(p,q) \le 1 0 ≤ H 2 ( p , q ) ≤ 1 H ( p , q ) = 1 2 ∣ ∣ p − q ∣ ∣ 2 H(p,q) = \frac{1}{\sqrt{2}}||\sqrt{p} - \sqrt{q}||_2 H ( p , q ) = 2 1 ∣ ∣ p − q ∣ ∣ 2
H 2 ( P , Q ) ≤ δ ( P , Q ) ≤ 2 H ( P , Q ) H^{2}(P,Q) \le \delta (P,Q) \le {\sqrt {2}}H(P,Q)
H 2 ( P , Q ) ≤ δ ( P , Q ) ≤ 2 H ( P , Q )
d ( x , y ) = ∣ ∣ x − y ∣ ∣ p = ( ∑ i ∣ x i − y i ∣ p ) 1 / p , p ∈ R d(x,y) = ||x-y||_p = \left(\sum_i|x_i - y_i|^p\right)^{1/p}, p\in \mathbb{R}
d ( x , y ) = ∣ ∣ x − y ∣ ∣ p = ( i ∑ ∣ x i − y i ∣ p ) 1 / p , p ∈ R
闵氏距离即向量范数,是最常见的距离定义。几个常见的特殊情况:
1-范数:曼哈顿距离 d ( x , y ) = ∣ ∣ x − y ∣ ∣ = ∑ i ∣ x i − y i ∣ ~~~~~~~~~~d(x,y) = ||x-y|| = \sum_i|x_i - y_i| d ( x , y ) = ∣ ∣ x − y ∣ ∣ = ∑ i ∣ x i − y i ∣
2-范数:欧氏距离 d ( x , y ) = ∣ ∣ x − y ∣ ∣ 2 = ∑ i ( x i − y i ) 2 ~~~~~~~~~~~~~d(x,y) = ||x-y||_2 = \sqrt{\sum_i(x_i - y_i)^2} d ( x , y ) = ∣ ∣ x − y ∣ ∣ 2 = ∑ i ( x i − y i ) 2
无穷范数:切比雪夫距离 d ( x , y ) = ∣ ∣ x − y ∣ ∣ ∞ = max i ∣ x i − y i ∣ ~~~d(x,y) = ||x-y||_\infty = \displaystyle\max_i|x_i - y_i| d ( x , y ) = ∣ ∣ x − y ∣ ∣ ∞ = i max ∣ x i − y i ∣
闵氏距离对称,且当p ≥ 1 p \ge 1 p ≥ 1
应用于分布,判断分布相似性,即统计距离:
总变差距离:1-范数应用于概率密度函数
?距离:2-范数应用于概率密度函数,没找到,χ 2 \chi^2 χ 2
K-S 检验:无穷范数应用于经验(累积)分布函数* *其他地方未看到过这个说法,存疑😋但仅从公式看是这样的。
应用于样本集,衡量样本与预测之间的偏差(预测误差):
直接使用:如最小二乘法中的欧氏距离∣ ∣ y − y ^ ∣ ∣ 2 = ∑ i n ( y i − f ( x i ) ) 2 ||y-\hat y||_2 = \sum_i^n (y_i - f(x_i))^2 ∣ ∣ y − y ^ ∣ ∣ 2 = ∑ i n ( y i − f ( x i ) ) 2
均方误差(MSE):MSE = 1 n ∣ ∣ y − y ^ ∣ ∣ 2 = 1 n ∑ i n ( y i − y ^ i ) 2 \operatorname{MSE} = \frac{1}{n} ||y-\hat y||_2 = \frac{1}{n} \sum_i^n(y_i-\hat y_i)^2 M S E = n 1 ∣ ∣ y − y ^ ∣ ∣ 2 = n 1 ∑ i n ( y i − y ^ i ) 2 问题 :(1)当指数p > 1 p>1 p > 1 p p p
为了克服闵氏距离,尤其是最常用的欧氏距离,应用于样本集时的缺陷,统计学家引入了马氏距离。
马氏距离(Mahalanobis Distance)
D M ( x , y ) = ( x − y ) T Σ − 1 ( x − y ) , Σ 为样本协方差矩阵 D_M(x,y) = \sqrt{ (x-y)^T \Sigma^{-1} (x-y)},~\footnotesize\Sigma \text{为样本协方差矩阵}
D M ( x , y ) = ( x − y ) T Σ − 1 ( x − y ) , Σ 为样本协方差矩阵
马氏距离由印度统计学家马哈拉诺比斯(P. C. Mahalanobis)提出,用于(分布未知的)样本集间相似度的度量。相比欧氏距离,马氏距离多了中间的协方差矩阵逆矩阵项,从而排除了特性间相关性的影响,且与尺度无关(方差归一化),不受量纲影响。
巴氏距离(Bhattacharyya Distance)
D B ( p , q ) = − ln ( ∑ i p i q i ) = − ln B C ( p , q ) D_{B}(p,q) = -\ln \left(\textstyle\sum_{i} \sqrt{p_iq_i}\right) = -\ln BC(p,q)
D B ( p , q ) = − ln ( ∑ i p i q i ) = − ln B C ( p , q )
B C ( p , q ) = ∑ i p i q i BC(p,q)=\textstyle\sum_{i} \sqrt{p_iq_i} B C ( p , q ) = ∑ i p i q i H 2 ( p , q ) = 1 − B C ( p , q ) H^2(p,q) = 1-BC(p,q) H 2 ( p , q ) = 1 − B C ( p , q )
Wasserstein距离(Wasserstein Metric / Earth Mover’s Distance)
W p ( μ , ν ) : = ( inf γ ∈ Γ ( μ , ν ) ∫ M × M d ( x , y ) p d γ ( x , y ) ) 1 / p , p ∈ [ 1 , ∞ ) W_{p}(\mu ,\nu) := \left(\inf_{\gamma \in \Gamma (\mu ,\nu)}\int_{M\times M}d(x,y)^{p}\,\mathrm{d}\gamma(x,y)\right)^{1/p}, ~~~ p\in[1, \infty)
W p ( μ , ν ) : = ( γ ∈ Γ ( μ , ν ) inf ∫ M × M d ( x , y ) p d γ ( x , y ) ) 1 / p , p ∈ [ 1 , ∞ )
在一阶矩情况下(p = 1 p=1 p = 1
W 1 ( μ , ν ) : = inf γ ∈ Γ ( μ , ν ) ∫ M × M d ( x , y ) d γ ( x , y ) = inf γ ∈ Γ ( μ , ν ) E ( x , y ) ∼ γ d ( x , y ) W_{1}(\mu ,\nu) := \inf_{\gamma \in \Gamma (\mu ,\nu)}\int_{M\times M}d(x,y)\,\mathrm{d}\gamma(x,y) = \inf_{\gamma \in \Gamma (\mu ,\nu)} \mathbb{E}_{(x,y)\sim\gamma} d(x,y)
W 1 ( μ , ν ) : = γ ∈ Γ ( μ , ν ) inf ∫ M × M d ( x , y ) d γ ( x , y ) = γ ∈ Γ ( μ , ν ) inf E ( x , y ) ∼ γ d ( x , y )
其中γ \gamma γ μ , ν \mu, \nu μ , ν Γ \Gamma Γ d ( x , y ) d(x,y) d ( x , y )
Wasserstein距离对称且满足三角不等式。
K-S检验(Kolmogorov–Smirnov Test)
D n = sup x ∣ F n ( x ) − F ( x ) ∣ D_n = \sup_x |F_n(x) - F(x)|
D n = x sup ∣ F n ( x ) − F ( x ) ∣
D n , m = sup x ∣ F 1 , n ( x ) − F 2 , m ( x ) ∣ D_{n,m} = \sup_x |F_{1,n}(x) - F_{2,m}(x)|
D n , m = x sup ∣ F 1 , n ( x ) − F 2 , m ( x ) ∣
其中F ( x ) F(x) F ( x ) F n ( x ) , F m ( x ) F_n(x),~F_m(x) F n ( x ) , F m ( x ) n , m n,~m n , m
K-S检验方法能够利用样本数据推断样本来自的总体是否服从某一理论分布,是一种拟合优度的检验方法,适用于探索连续型随机变量的分布。单样本K-S检验的原假设是:样本来自的总体与指定的理论分布无显著差异。
原假设下,n → ∞ n\to \infty n → ∞ n D n \sqrt{n} D_n n D n K = sup t ∈ [ 0 , 1 ] ∣ B ( t ) ∣ , B ( t ) K=\displaystyle\sup_{t\in [0,1]}|B(t)|, B(t) K = t ∈ [ 0 , 1 ] sup ∣ B ( t ) ∣ , B ( t )
n D n → n → ∞ sup t ∣ B ( F ( t ) ) ∣ \sqrt{n} D_n \xrightarrow {n\to \infty } \sup_{t}|B(F(t))|
n D n n → ∞ t sup ∣ B ( F ( t ) ) ∣
Kolmogorov分布的累计分布形式为:
Pr ( K ≤ x ) = 1 − 2 ∑ k = 1 ∞ ( − 1 ) k − 1 e − 2 k 2 x 2 = 2 π x ∑ k = 1 ∞ e − ( 2 k − 1 ) 2 π 2 / ( 8 x 2 ) \Pr (K\leq x)=1-2\sum_{k=1}^{\infty }(-1)^{k-1}e^{-2k^{2}x^{2}}={\frac{\sqrt {2\pi }}{x}}\sum_{k=1}^{\infty }e^{-(2k-1)^{2}\pi^{2}/(8x^{2})}
Pr ( K ≤ x ) = 1 − 2 k = 1 ∑ ∞ ( − 1 ) k − 1 e − 2 k 2 x 2 = x 2 π k = 1 ∑ ∞ e − ( 2 k − 1 ) 2 π 2 / ( 8 x 2 )
可由Kolmogorov分布获得判断拟合好坏的临界值。n D n > K α \sqrt{n} D_{n}>K_{\alpha } n D n > K α α \alpha α K α K_{\alpha} K α Pr ( K ≤ K α ) = 1 − α \Pr (K\leq K_{\alpha })=1-\alpha Pr ( K ≤ K α ) = 1 − α
对于两个样本,D n , m > c ( α ) n + m n m D_{n,m}>c(\alpha) \sqrt{\frac{n+m}{nm}} D n , m > c ( α ) n m n + m α \alpha α c ( α ) = − 1 2 ln ( α 2 ) c\left(\alpha \right)= \sqrt{-{\frac{1}{2}}\ln \left({\frac{\alpha}{2}}\right)} c ( α ) = − 2 1 ln ( 2 α )
χ 2 \chi^2 χ 2 KS 检验都是统计学中常见的非参数检验方法,用于检验两个分布(数据与模型或数据与数据)的近似程度,χ 2 \chi^2 χ 2 χ 2 \chi^2 χ 2 KS 检验判据则来自Kolmogorov分布。χ 2 \chi^2 χ 2
最大均值差异(Maximum Mean Discrepancy, MMD)
MMD ( p , q ) : = sup f ∈ F ( E p [ f ( x ) ] − E q [ f ( y ) ] ) \operatorname{MMD}(p,q) := \sup_{f \in \mathcal{F}}(E_p [f(x)] - E_q [f(y)])
M M D ( p , q ) : = f ∈ F sup ( E p [ f ( x ) ] − E q [ f ( y ) ] )
F \mathcal{F} F F = C 0 ( X ) \mathcal{F}=C^0(\mathcal{X}) F = C 0 ( X ) X \mathcal{X} X
MMD ( X , Y ) = sup f ∈ F ( 1 m ∑ i m f ( x i ) − 1 n ∑ i n f ( y i ) ) \operatorname{MMD}(X,Y)=\sup_{f \in \mathcal{F}}( \frac{1}{m} \sum_i^m f(x_i) - \frac{1}{n} \sum_i^n f(y_i))
M M D ( X , Y ) = f ∈ F sup ( m 1 i ∑ m f ( x i ) − n 1 i ∑ n f ( y i ) )
MMD ( X , Y ) = ∥ ∑ i = 1 n 1 f ( x i ) − ∑ j = 1 n 2 f ( y j ) ∥ H 2 \operatorname{MMD}(X,Y)=\left \Vert \sum_{i=1}^{n_1} f(x_i)- \sum_{j=1}^{n_2} f(y_j) \right \Vert^2_\mathcal{H}
M M D ( X , Y ) = ∥ ∥ ∥ ∥ ∥ ∥ i = 1 ∑ n 1 f ( x i ) − j = 1 ∑ n 2 f ( y j ) ∥ ∥ ∥ ∥ ∥ ∥ H 2
最大均值差异是应用于样本而非分布函数,其基本想法为:如果两个分布的随机样本对任意的函数f f f
主要用于迁移学习,稍微有点复杂,为了真正理解上述公式,需要首先了解再生核希尔伯特空间(RKHS),可以参考这篇文章
均方误差(MSE)在参数估计中也存在,但文中与此处不同:假设未知参数θ \theta θ θ ^ \hat\theta θ ^ M S E ( θ ^ ) = Var θ ^ ( θ ^ ) + Bais θ ^ ( θ ^ , θ ) 2 MSE(\hat\theta) = \operatorname{Var}_{\hat\theta}(\hat\theta) + \operatorname{Bais}_{\hat\theta}(\hat\theta, \theta)^2 M S E ( θ ^ ) = V a r θ ^ ( θ ^ ) + B a i s θ ^ ( θ ^ , θ ) 2 θ ^ \hat\theta θ ^ M S E ( x ) = E [ ( x − x t ) 2 ] = σ x + ( x ˉ − x ) 2 MSE(x) = E[(x-x_t)^2] = \sigma_{x} + (\bar{x}-x)^2 M S E ( x ) = E [ ( x − x t ) 2 ] = σ x + ( x ˉ − x ) 2
注 :统计中常见的数据可分为分类数据 ( Categorical Variable ) 和数值数据 ( Numerical Variable ) ,大致可理解为定性(qualitative)和定量(quantitative)数据。其中分类数据又可分有序(Ordinal)和无序(Nominal);数值数据可分离散(Discrete)和连续(Continuous)。
扩展阅读: 评分卡系列(三):分类学习器的评估