NLP基本概念II：Attention! 机器翻译中的注意力机制

Posted on In , Views: Waline:

NLP基本概念系列将以嵌入(Embedding)、注意力(Attention)、生成(Generation)以及Transformer为核心，梳理NLP任务相关的基础概念。在NLP基本概念I中介绍了NLP从词嵌入到预训练模型的发展历史，其中注意力机制对大规模预训练模型的兴起起到了关键作用，本文将以机器翻译为出发点，梳理注意力机制的发展历史，具体涉及统计机器翻译STM、条件语言模型、对齐(alignment)、神经机器翻译NTM、Seq2Seq、注意力、自注意力、QKV诠释等概念。
主要参考：Stanford CS224n (2021) P7-P9
Attention? Attention!、Seq2Seq and Attention

机器翻译

统计机器翻译SMT

90年代前机器翻译(Machine Translate, MT)主要采用基于规则的方式，到了90年开始统计方法(Statistical, SMT)逐渐占据主流。基本思想是要实现语言序列xx到yy的翻译，在统计上可表示为给定输入序列xx，找到其对应的概率最大的输出序列yy，即arg max⁡yP(y∣x)\small \argmax_y P(y|x)。这种给定条件xx下计算序列概率P(y∣x)\small P(y|x)的任务被称为条件语言模型(Conditional LM)。作为对比，普通语言模型的目标是直接计算某个语言序列的概率P(y)\small P(y)而非条件概率。

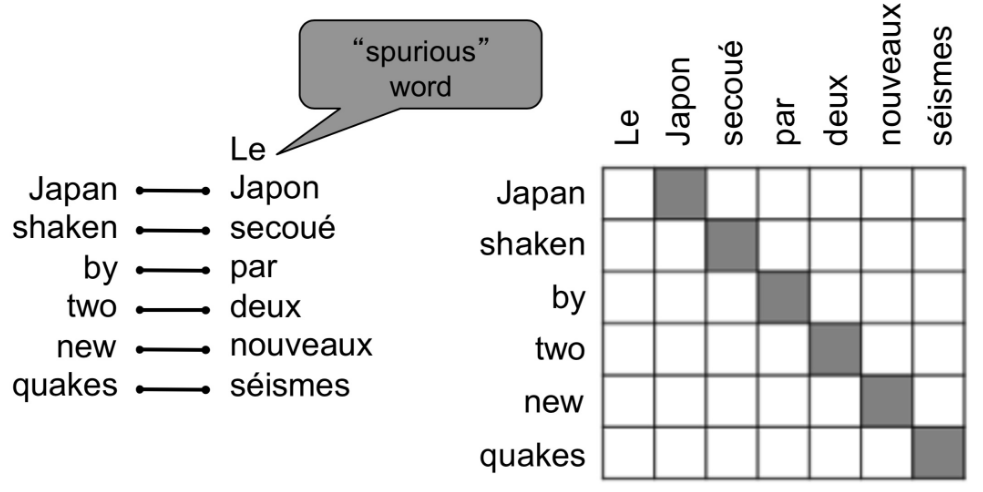
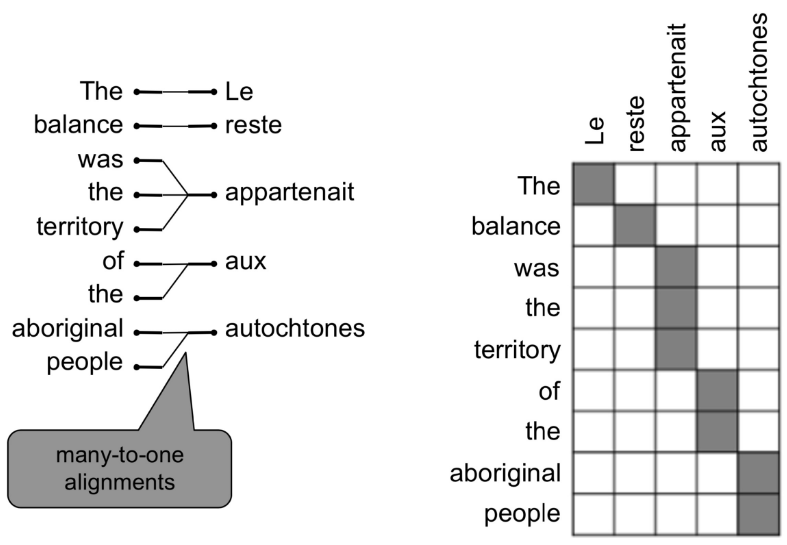
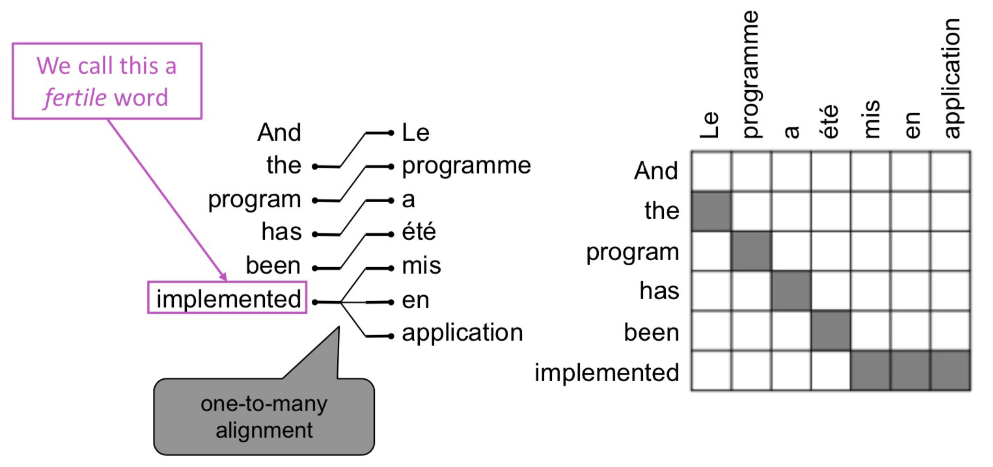
语言模型的核心问题只是语句中词语间依赖关系的统计建模，可简化为n-gram语言模型；而条件语言模型核心问题则是源语言与目标语言序列间的对应关系。最简单粗暴的做法是遍历所有可能输出序列，找到概率最大的那个，这显然不现实。更自然的选择是将语句序列拆解为单词，找到不同语言在单词或短语级别的对应关系，即所谓对齐(alignment)。这依然不是一个简单的任务，不同语言表达同一个意思的语句，所涉及词汇的数量和顺序上都是存在差异的，而不是简单的一一对应(align)，逐个单词的直译显然不是明智的选择。相较于一一对应，更可能的是一对多、多对一、多对多(短语间对应)等情况，还有某些虚词可能没有对应，而对齐需要考虑到所有这些不同位置和数量上的对应信息，以及具体语句的上下文语境。

Alignment(source: CS224N)

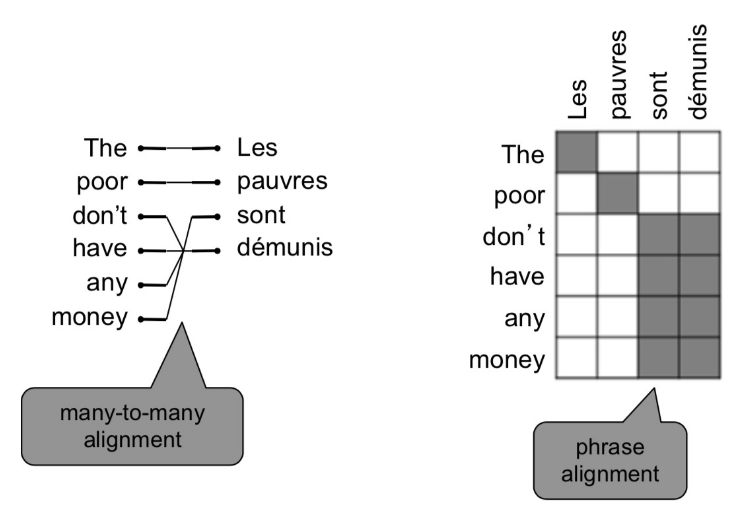
在统计语言模型做法中，基于贝叶斯法则P(y∣x)=P(x∣y)p(y)p(x)\small P(y|x) = \frac{P(x|y)p(y)}{p(x)}，给定xx对yy计算argmax，P(x)\small P(x)可视为常数，arg max⁡yP(y∣x)=arg max⁡yP(x∣y)p(y)\small \argmax_y P(y|x) = \argmax_y P(x|y)p(y)。这其中P(y)\small P(y)为目标语言自身的语言模型，可通过n-gram语言模型解决，具体可参考NLP基本概念I；而P(x∣y)\small P(x|y)则是所谓的翻译模型，传统做法是，引入代表对齐信息的隐变量aa，将P(x∣y)\small P(x|y)转换为P(x,a∣y)\small P(x,a|y)，建立隐马尔科夫模型(HMM)等隐变量模型，并借助EM算法等专门算法优化。这一过程需要大量的手动特征工程，额外的同义短语库维护，对每对语言的针对性处理以及大量复杂的专用子模块等等，是非常复杂的软件工程。（机器翻译中x,yx,y理论上应该是对偶的，不是很理解这里使用贝叶斯的意义，为什么必须将P(y∣x)\small P(y|x)转换为P(x∣y)\small P(x|y)，而不直接引入对齐隐变量计算P(y,a∣x)\small P(y, a|x)？是因为x,yx,y的语料资源不对等？）

神经机器翻译NMT

Nal Kalchbrenner和 Phil Blunsom 于2013年首先提出基于神经网络的翻译方法(Neural MT, NMT)，使用CNN作为编码器，RNN作为解码器，首次实现了自然语言的端到端翻译。随后Cho et al.(2014)提出Encoder-Decoder结构，将两个RNN分别作为编码器和解码器构建神经网络模型，并将其融入传统统计机器翻译(SMT)，网络经过训练后用于为短语对打分。虽然文中提到可直接用神经网络替代SMT，但基于计算量考虑，作者未尝试这种做法。而数月后，Sutskever等人将其实现，提出了Seq2Seq模型，将两个LSTM分别作为编码器和解码器，直接实现序列到序列的机器翻译，借助四层LSTM结合反向输入技巧，Seq2Seq获得了超越统计翻译的表现。Cho等人没有放弃SMT，感觉棋差一招，不过普通RNN相对LSTM确实更难训练，Seq2Seq中也指出用RNN实验没成功。

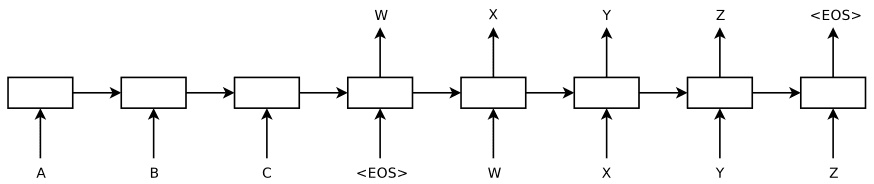
Seq2Seq(source: Sutskever et al. 2014)

这种编码器+解码器的结构在NLP之外其实早已存在，最典型的就是自编码器，只是不同于前者，Seq2Seq中输入和输出通常都不是同一个序列，在机器翻译中就是翻译的源语言序列与目标语言序列。在Seq2Seq之前，单独的RNN网络虽然可方便的应对输入或输出序列长度不定的问题，能有效处理N-to-1、1-to-N以及N-to-N问题，但对于输出和输出长度都不定的N-to-M问题却依然难以应对，机器翻译刚好属于该问题。这种编码器+解码器(Seq2Seq)的架构，并不算复杂(如上图所示)，却有效破解了这类N-to-M的问题，而且通过变换解码器可适应多种问题。因此Seq2Seq作为神经机器翻译的标准结构提出后，迅速扩展至各种自然语言处理任务，如摘要生成、对话系统以及传统语言学中的句法剖析标注，以及代码生成(自然语言与代码之间的翻译)等任务。

与SMT相同，NMT依然属于条件语言模型，其中解码器部分为语言模型，逐个单词的预测目标语句，同时其解码器又建立在编码器输出之上。不过不同于SMT，在NMT中无需再基于贝叶斯进行转换，也无需引入额外的隐变量代表对齐信息，模型在训练时的优化目标为arg max⁡θ log⁡P(y^=y∣x,θ)\small \argmax_{\theta} ~ \log P(\hat{y}=y|x,\theta)，而在翻译时的目标是arg max⁡y log⁡P(y∣x,θ)\small \argmax_{y} ~ \log P(y|x,\theta)。

在2013-2016年左右，SMT依然是当时的主流，并由最初基于单词的(word-based)模型发展为基于短语的(phrase-based)和基于句法分析标注的(syntax-based)模型，但同时也已陷入瓶颈，难以获得明显提升。NMT在最初出现时，只是接近当时的水平，并无显著优势，但到了2016年NMT就已成为主流选择，并很快拉开了与SMT的差距。尤其是考虑到SMT需要大量的人工特征提取，复杂的模块整合，而NMT只需要端到端的训练，这一成就更是惊人的，这其中很大一部分功劳属于注意力机制。

注意力Attention

we conjecture that the use of a fixed-length vector is a bottleneck in improving the performance of this basic encoder-decoder architecture, and propose to extend this by allowing a model to automatically (soft-)search for parts of a source sentence that are relevant to predicting a target word, without having to form these parts as a hard segment explicitly.

在Seq2Seq中我们将编码器最终的隐变量输出视为整个输入语句的语义编码传递给解码器解码，成功破解了机器翻译时输入输出数量不对等的困难。但人们很快意识到编码器与解码器间仅通过单个隐变量交流，信息容量有限，存在信息瓶颈问题，随着输入句子的增长，翻译精度就会下降。如何更好的利用编码器其他的隐状态是解决问题的关键，一种思路是将RNN的隐状态理解为当前单词在其上文语境中(没有下文)的嵌入表示，将编码器所有隐状态整合(如取平均)后再传给解码器，这是文本理解分类任务中有效的做法，但其信息容量依然受限于隐变量维度。Bahdanau等人很快就找到了更全面利用编码器隐状态的方法，提出了注意力机制(虽然并没有命名为注意力)。(注：注意力和Seq2Seq两篇文章几乎同时出现，arxiv上传只差一周，而且相互引用)。

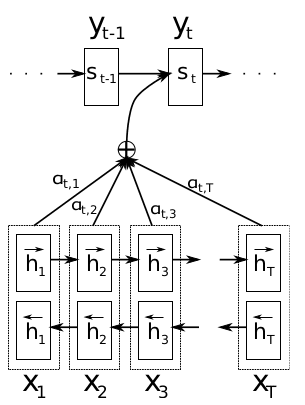
Attention(source: Bahdanau et al. 2014)

图中下面为编码器，为双向RNN结构，上面为解码器，为单向RNN。在NLP基本概念I已经介绍，在自注意力机制提出之前，双向RNN是获取语境嵌入的最佳选择。使用两个独立的RNN，分别由前向后和由后向前读取序列计算隐状态，之后将两者隐状态拼接在一起作为最终语义编码。双向RNN能获取更全面的语境信息，不过只适用于文本理解任务，而不能用于文本生成任务，后者需要基于上文生成下文，双向RNN将导致信息泄露。因此图中编码器采用双向RNN，而解码器只能用单向RNN。

编码器与解码器之间关联不再是普通Seq2Seq的单个隐变量，而是针对每个解码器的输出有选择的整合所有编码器隐状态，作为解码器输入，即所谓注意力机制。具体的，模型会基于当前编码器隐状态st−1s_{t-1}和解码器的所有隐状态hk,k∈(1,...,T)h_k, k\small\in (1,...,T)计算关联度评分etke_{tk}，之后使用softmax转换为注意力权重atka_{tk}，最后将编码器所有隐状态加权求和后作为当前解码器输出对应的语境向量ctc_{t}，传递给解码器解码。

  • 关联度评分(alignment score)：etk=NN(st−1,hk)=vTtanh⁡(Wst−1+Uhk)e_{tk} = \text{NN}(s_{t-1}, h_k) = v^T\tanh(Ws_{t-1} + U h_k)
  • 注意力权重(attention weight)：atk=exp⁡(etk)∑jexp⁡(etj)a_{tk} =\small \displaystyle \frac{\exp(e_{tk})}{\sum_j \exp(e_{tj})}
  • 上下文向量(context vector)：ct=∑katkhkc_{t} = \sum_{k} a_{tk} h_k
  • 解码器解码(LSTM/GRU)：st=f(st−1,yt−1,ct)s_t = f(s_{t-1}, y_{t-1}, c_t)

相比传统Seq2Seq的主要区别在于每个解码器状态sts_t的产生都有不同上下文向量ctc_t的参与。即通过注意力机制，解码器生成每个单词时都有选择的从输入语句中提取到与输出最相关的信息，成功打破了Seq2Seq传递单个隐变量的信息瓶颈。而且这种对于输入的选择性关注是在模型训练时自动学习得到的，在Bahdanau的文章中使用简单的MLP建立这种选择性，vTtanh⁡(Wst−1+Uhk)v^T\tanh(Ws_{t-1} + U h_k)，其中v,W,Uv, W, U均为模型可训练的参数。

人类查看图片或阅读文字时会根据自己的需求或兴趣点分配注意力，快速定位关键信息。而上面这种基于输出对输入信息进行选择性抽取的做法与人类观察事物时的注意力分配非常类似，因此被称为注意力(Attention)。对于机器翻译任务，注意力机制是寻找与当前输出词汇最相关的输入词汇，在某种程度上与传统统计模型中的对齐信息非常接近，不同的是这里的注意力不再是隐变量，是作为模型结构的一部分可以直接得到训练，这就是文章标题“NTM by Jointly Learning to Align and Translate”中同时学习对齐和翻译的含义。

Bahdanau et al. (2014)中通过加权实现输入输出对齐的思路直接源自Graves (2013)，后者在处理手写识别任务中，为实现字符与识别结果的对齐提出了软窗口及窗口权重的概念。同样是通过对输入元素加权调整产生特定输出的“注意力”分配，区别在于Graves (2013)中的权重为(混合)高斯函数，且考虑到手写识别是单向对齐，随着输出预测(高斯)窗口中心会进行单向移动；Bahdanau et al. (2014)中将权重计算替换为MLP，且不存在窗口中心的移动，权重完全由输入及输出决定。最后，这种根据输出调整对输入关注权重的注意力概念在CV领域也早有应用，不过却是随着在NLP领域的应用，尤其是Transformer的提出而得以流行。

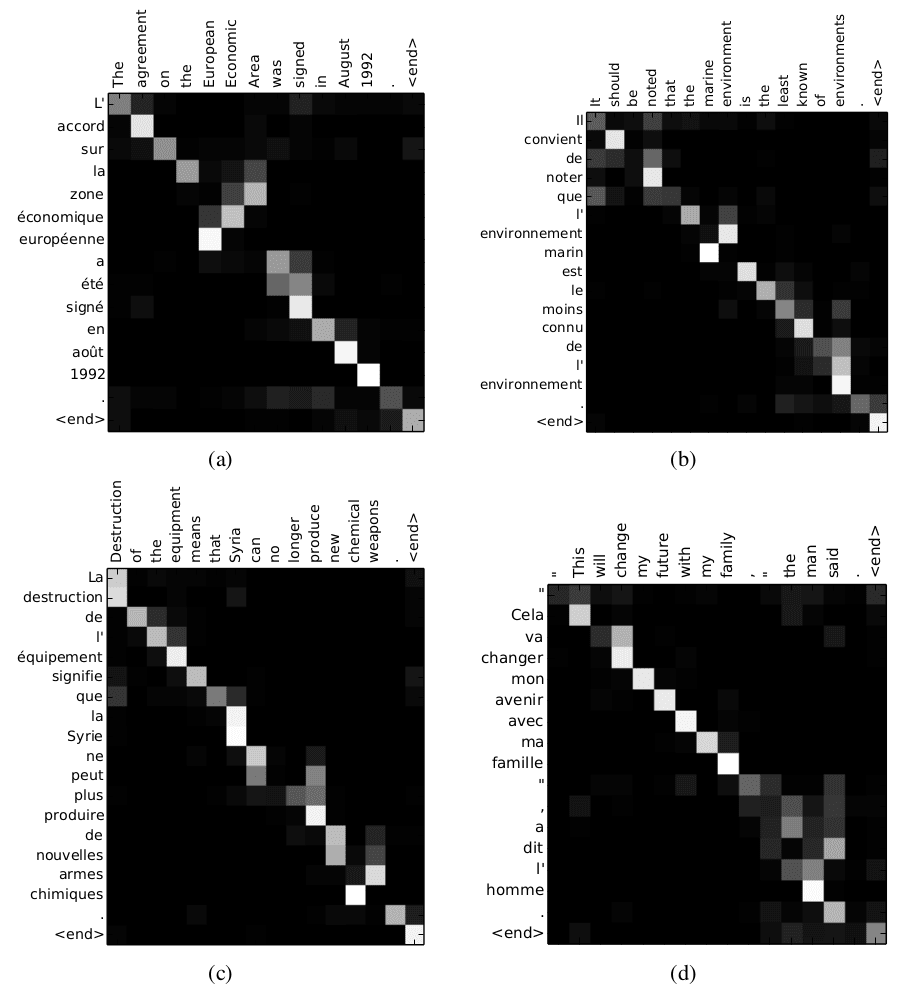
注意力机制解决了传统Seq2Seq的信息瓶颈，提供了信息传递的捷径，有助于更有效的获取长程信息以及梯度更新的反向传递，并且可解释性比之前的简单Seq2Seq更强，如下图所示，注意力权重的可视化非常直观的反映了不同语言序列间的对齐信息。

The proposed approach provides an intuitive way to inspect the (soft-)alignment between the words in a generated translation and those in a source sentence. This is done by visualizing the annotation weights.

Alignment(source: Bahdanau et al. 2014)

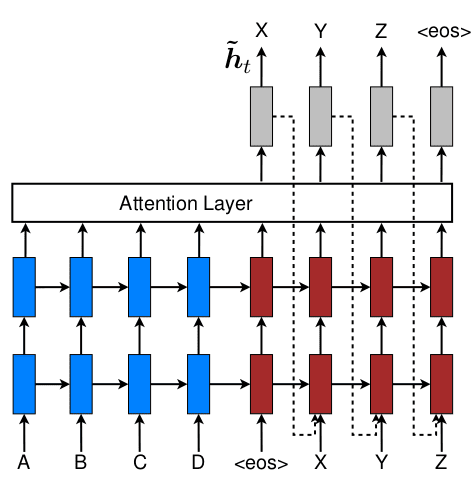
在注意力机制被引入Seq2Seq模型后，初期一直是作为模型的“附属”：编码器和解码器通常是循环网络(LSTM/GRU)，注意力机制仅作为两个循环网络沟通的桥梁。同时人们也提出了内部注意力/自注意力的概念(如Cheng et al. 2016)，用于编码器/解码器内部关联分析，与编解码器之间的注意力配合，但整体依然是建立在循环网络之上。2017年，Vaswani等人首次提出完全舍弃循环网络，仅借助注意力机制(和普通MLP)实现的Seq2Seq构架，即所谓的“Attention is all you need”。关于模型的具体构架，即Transformer结构，可参考NLP基本概念IV的介绍，这里只关注用于替换循环网络的自注意力机制。虽然自注意力的概念不是在Transformer中首先提出，但确实是通过Transformer被人们所熟知，因此提到自注意力机制最常提到的就是“Attention is all you need”这篇文章。

在分配注意力时，我们要有查看的对象，还要有关注的目标。以查看图片为例，如果我们有预设的关注目标，目标源于内容之外，就是所谓的互注意力。而如果不预设目标，通过对画面的观察确定画面元素间的关联性，此时关注的目标可以是画面的任何元素，而查看的内容同样是画面所包含的元素，目标与对象源自同一主体，两两相互关联，即所谓自注意力。在机器翻译中，从目标语言单词出发，计算其与源语言序列各词语间关联性，属于互注意力，而源语言内部元素间的关联性则属于自注意力。

Self Attention(source: Cheng et al. 2016)

上面这幅图展示了自注意机制：图中红色为当前关注目标，蓝色则代表注意力分配，关注目标与内容来自同一句话。而由于使用了单向的RNN，模型只会注意左侧文本。可以看到当关注到run时，模型重点注意了相距较远的FBI(其实更应该关注Criminal，还是不准)。

自注意力相比传统RNN能更便捷的获取长程关联信息，但在自身出色的关联信息抽取能力之外，更为重要的是基于自注意力的Transformer结构成功打破了RNN无法并行的难题，支持并行加速。而且由于抛弃了RNN，(自)注意力的计算也不再建立在RNN隐状态之上，而是直接建立在词向量之上。唯一的缺点是自注意力位置无关的特性使模型失去了时序/位置信息，这点通常是通过引入位置编码加以改善。

早期发展

从最初Seq2Seq中编码器与解码器之间实现对齐的注意力机制，到Transformer中替换循环网络的自注意力机制，注意力发展出了诸多变种，出现诸如加法注意力/乘法注意力、软注意力/硬注意力、局部注意力/全局注意力、多头注意力等等概念。早期的注意力通常是建立在词向量序列经过RNN后处理得到隐变量之上，而主要过程可分三步，而早期的发展也主要集中于这三点的选择。

  • 关联度评分(alignment score)/匹配评分(matching score)：etk=f(st,hk)e_{tk} = f(s_t, h_k)
    有很多不同选择，主要的是乘法/内积(Luong style)和加法(Bahdanau style)两种。

  • 注意力权重(attention weight)：atk=exp⁡(etk)∑jexp⁡(etj)a_{tk} = \small\displaystyle \frac{\exp(e_{tk})}{\sum_j \exp(e_{tj})}
    变化不多，基本就是softmax函数，主要作用是将评分(有正有负，无法直接归一化)进行概率归一化。根据softmax的对象也可分局部或全局注意力(Luong et al. 2015)。

  • 上下文向量(context vector)：ct=∑katkhkc_{t} = \sum_{k} a_{tk} h_k
    变化不多，基本就是加权求和，不过在硬注意力(Xu et al. 2015)中选择将注意力权重视为概率，通过采样求和降低计算量。

加法 v.s. 乘法

关联度评分的计算是注意力机制的核心，有很多不同变种，主要是加法和乘法两种。由于关联度评分是在关注目标(sts_{t})与关注内容(hkh_{k})之间计算，所谓的加法和乘法也是指的sts_{t}与hkh_{k}的运算方式。

  • 加法注意力(additive)：etk=vTtanh⁡(Ust+Vhk)e_{tk} = v^T \tanh(Us_{t} + Vh_{k})
    最初版本的注意力(Bahdanau et al. 2014)，本质上是一个简单的MLP网络，v, U, V为模型参数，其中向量v的维度(及U, V的相应维度)是一个可调的超参数。由于sts_{t}与hkh_{k}间为加法运算通常被称为加法注意力，也被称为Bahdanau-style注意力。

  • 内积/乘法注意力(dot-product)：etk=stThke_{tk} = s_t^T h_{k}
    Luong et al. 2015中提出的简化版注意力，直接取两个隐状态的内积。内积在某种程度上反映了向量的相似度，以这种相似度作为关联度的度量，简单直观，相比最初版本的MLP，简化计算的同时也具有更好的可解释性。由于采用内积运算，被称为内积注意力或乘法注意力，此外也被称为Luong-style注意力。

  • 内积推广/双线性注意力(general bilinear)：etk=stTWhke_{tk} = s_{t}^T W h_{k}
    上述内积注意力虽然简单直观，但限制了st,hks_t, h_k两个向量长度必须一致，因此Luong在提出内积注意力的同时，做了简单推广，WW的引入使st,hks_t, h_k又恢复自由。

Bahdanau et al. 2014 (left) v.s. Luong et al. 2015 (right)
除了加法注意力和内积注意力，Bahdanau et al.与Luong et al.在注意力计算上有一些细节值得注意。对于关联评分，前者是在st−1s_{t-1}与hkh_k间计算，而后者则是在sts_{t}与hkh_k间计算。这样的区别源于计算tt时刻输出时，前者的sts_t是由st−1s_{t-1}及ctc_t(注意力加权的上下文向量)计算得到。后者sts_{t}是解码器由普通RNN计算得到(图中红色部分)，之后在解码器输出前引入注意力机制，由st,hks_t, h_k计算得到ctc_t，再由st,cts_t, c_t得到新的隐状态(图中h~t\tilde{h}_t)，用于产生最终输出。

软硬注意力

在注意力计算中，得到相关度评分后，会使用softmax函数进行概率归一化得到最终的注意力权重，给每个输入都分配一定的权重。考虑到当输入序列过长，如整个段落或文章时，对所有输入计算注意力不仅计算量大，而且也可能没必要(真正重要的信息可能被淹没在很多权重低但数量多的无关信息中)。
考虑到softmax是argmax的soft版，如果将softmax替换为argmax则走向另一极端，每次只关注单个输入。Xu et al. 2015中提出的方案则是将注意力权重作为概率，从所有输入中随机采样取一部分用于上下文向量计算。硬注意力不像argmax那么极端，也不像softmax权重考虑所有输入，优点是在模型应用阶段的计算量少，但其缺点在于不再在可微，训练阶段需要借助方差缩减或强化学习等复杂技术实现优化，因此此后采用不多。

局部注意力

受到软硬注意力的启发，Luong等人提出了局部注意力，同样是针对关注目标，每次只选取最相关的少部分文本用于注意力计算。但不同于硬注意力通过随机采样选择输入(零散的个体)，Luong通过设置窗口选择输入(连续的局部)。局部注意力在减少全局注意力的计算量的同时，避免了硬注意力不可微分的缺点。

Global Attention v.s. Local Attention(source: Luong et al. 2015)

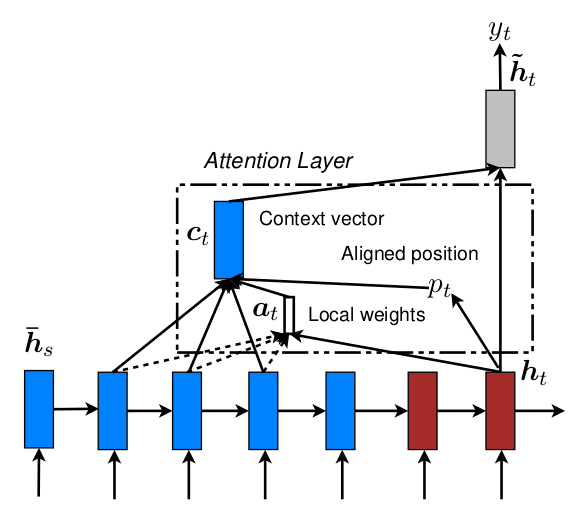
为计算局部注意力，需引入额外参数描述窗口位置及大小：窗口以ptp_t为中心，左右宽度dd。其中窗口大小为超参数，窗口位置则窗口函数决定：

  • pt=tp_t =t，即取窗口位置与解码器器输出对齐 (monotonic alignment, local-m)
    对应取编码器隐状态hk,k∈[t−d,t+d]\small h_k, k \in[t-d, t+d]，越界直接忽略，atk=exp⁡(etk)∑jexp⁡(etj)a_{tk} = \small\displaystyle \frac{\exp(e_{tk})}{\sum_j \exp(e_{tj})}。
  • pt=T σ(vTtanh⁡(Wst))p_t= {\small T} ~ \sigma(v^T \tanh({\small W}s_t)) (predictive alignment, local-p)
    其中T{\small T}为编码器出入序列长度，v,Wv, {\small W}可由模型学习的自由参数，注意ptp_t并没有取整，就是浮点数。在计算注意力权重时，作者在正常的softmax函数之外还叠加了以ptp_t为中心的正态分布，进一步调整权重：atk=exp⁡(etk)∑jexp⁡(etj) exp⁡(−(k−pt)22σ2)a_{tk} = \small\displaystyle \frac{\exp(e_{tk})}{\sum_j \exp(e_{tj})} ~ \exp(-\frac{(k-p_t)^2}{2\sigma^2})，其中σ\sigma被取为d/2d/2。
    其中σ(vTtanh⁡(Wst)\sigma(v^T \tanh({\small W}s_t)本身类似于计算只考虑关注目标的注意力：只涉及一个向量，无法用内积计算方式，此处采用了Bahdanau中所使用的前馈网络；同时不再用两两关联，softmax也退化为sigmoid。但这种只考虑关注目标，不考虑内容就得到的关注位置ptp_t，感觉合理存疑，只能期望训练时模型调整参数以使ptp_t取到合理位置。这或许也是为什么局部注意力应用不是很广的原因之一。

QKV诠释

Vaswani等人基于自注意力提出Transformer结构的同时，还引入了Query, Key, Value的概念，并成为当前理解注意力机制事实上的标准，不少地方介绍注意力机制时都直接从QKV向量开始，而不提其他。

An attention function can be described as mapping a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors. The output is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key.

在计算注意力时需要有“目标”向量和“内容”向量来计算关联度评分，softmax归一化得到注意力权重后，再对所有“内容”向量加权得到上下文向量。对于自注意力，目标与内容都来自输入，而这一过程需要使用三次输入向量。为进行区分，QKV诠释中将三次用到的向量分别称为Query，Key, Value。Query就是关注目标，Key/Value属于关注内容，Key与Value一一对应，但两者内容可以不同，可大致将Key视为Value的压缩表示。

QKV诠释中这些概念其实是对数据检索系统的借鉴：在数据库领域，我们通常会通过对数据内容(Value)建立关键字(Key)索引，加快数据的检索访问(Query)。在检索数据时通过匹配检索要求(Query)与关键字(Key)，找到匹配的关键字，并返回对应的具体内容(Value)。从这个角度，所谓注意力机制也可以理解为某种内存访问机制，只不过返回的是全部地址内存的加权和，而非特定地址的内存，这种“软”的访问机制的最大优势在于可微分，因此可通过神经网络的反向传播进行训练。

在QKV诠释中，注意力的关联度评分建立在Query和Key之上，而上下文向量则是通过对Value加权得到。当Query和Key来源相同就属于自注意，当Query和Key来源不同就属于互注意力。对照前面的互注意力，sts_t就对应与Query，hkh_k则同时对应此处的Key和Value。

理解投影

需要注意QKV诠释中的引入Q, K, V三组向量只是为了方便区分和解释，并不需要真的是完全不同的向量。在最初Transformer文章中的自注意力机制的Q, K, V其实都对应输入，因此是没有投影操作的(也就完全没有参数)。正因如此，在对比自注意力机制与RNN/CNN计算量时是没有考虑投影操作的。而在多头自注意力中，如果依然不进行投影，各个头的自注意部分将完全相同(没有参数)，因此分别进行了投影操作，投影矩阵与Q, K, V相乘，Q, K, V本身依然是对应相同的输入。不过在随后发展中，这种对输入分别投影的操作成为默认选择，Q, K, V也就通常指代投影后向量q=Wqx,k=Wkx,v=Wvxq = W_q x, k = W_k x, v = W_v x。

为什么需要qkv三个向量
那么除了在多头注意力中引入各自独立的参数，还有哪些进行分别投影的理由吗？这里从内积注意力的角度对投影的合理性进行简单分析。先假设不引入q,k,vq, k, v向量，直接从词向量xx出发计算注意力。向量内积反映了词向量的相似度，对于自注意力，不投影而直接用词向量，会使得注意力过多的集中于词语自身。相反上下文关联词语的相似度可能并不高，比如作为主语的名词和作为谓语的动词，以及修饰名词的形容词和名词本身，这些词在句子中是有很强关联性的，但相似度却并不会很高(词性不同)，因此最好能有词向量之外更灵活的向量表示来计算注意力权重。

通过线性变换得到q,kq, k可理解为在上下文语境中对词向量进行投影(“再嵌入”)，通过模型训练中对变换矩阵的学习得到真正反映上下文关系的向量表示。这解释了q,kq, k的必要性，但为什么要区分kk和vv？q,kq, k由于要进行内积操作，维度必须一致，而代表内容向量维度可能很高，通过区分kk和vv，可以使k,qk, q的维度一致的同时相对于内容向量vv保持灵活性，如选择较低维度。但vv真的有必要吗？为什么不直接将输入xx用作vv，这点确实不是很理解，可能是vv相对xx也可以压缩维度，同时增加模型灵活性。最后配合多头注意力，可实现每个头各自不同的关注点。如下图中，两组独立的注意力操作，左侧的更倾向于关注自身及附近，右侧则倾向于关注上下文，而非自身。

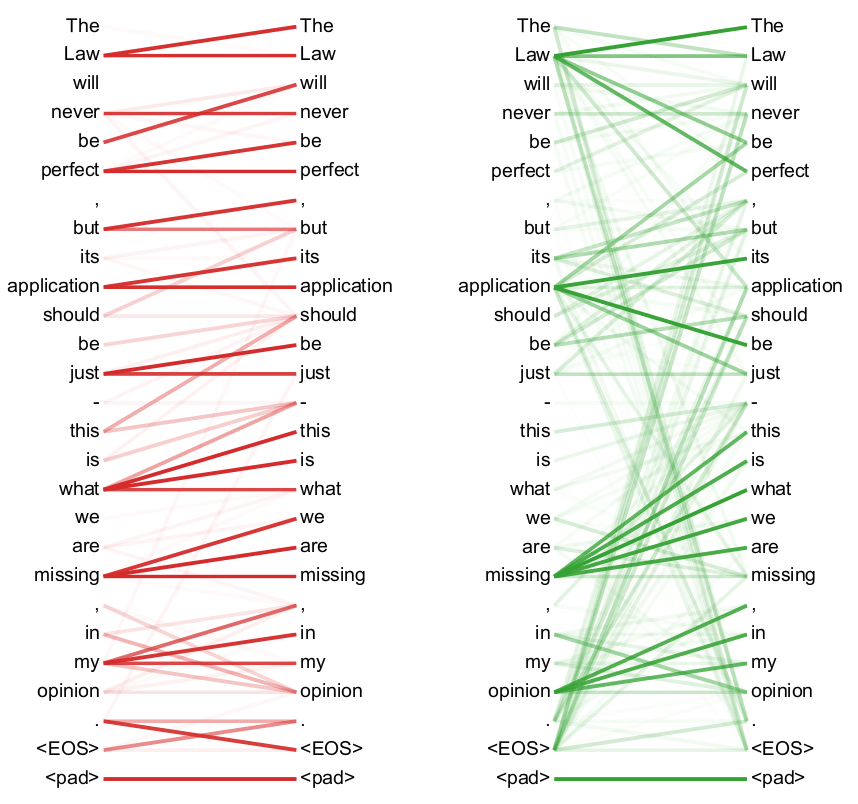
Multihead Atttention (source: Vaswani et al. 2017)

另一方面，从互注意力角度理解，关注的目标(target)xtx_t与内容(content)xcx_c两者长度很可能是不一致的，需要转换后才能进行内积运算，即使用推广的内积操作xtTWxcx_t^T {\small W} x_c。考虑到词向量xt,xcx_t, x_c的维度一般都比较大，矩阵W\small W的参数量也会很大，为降低参数量，可以选择进行一个低秩分解将W∈Rdt×dc\small W\in\R^{d_t \times d_c}拆解为UTV,U∈Rk×dtv∈Rk×dc\small U^T V, U\in\R^{k\times d_t} v\in\R^{k\times d_c}，只要取k≪dt,dck \ll d_t, d_c就可以压缩参数量。相应的xtTWxc=xtT UTV xc=(Uxt)T Vxc\small x_t^T W x_c = x_t^T ~U^T V~ x_c = (Ux_t)^T ~ Vx_c，这其实就是QKV诠释中获取q,kq, k向量所做的投影，U\small U对应Wq\small W_q、V\small V对应Wk\small W_k。

根据上述分析，为降低参数量，QKV的向量维度通常是要比输入向量小，当然并非必须。Transformer中还引入了多头注意力，即同样的操作独立(并列)执行多次，最终合并输出：不同头的注意力被拼接在一起，并整体投影后作为最终输出。具体的Transformer所使用的QKV向量长度为64，要比词向量长度512小很多，这样可使得多头注意力(N=8)计算量大致与QKV取521的单头注意力大致相当。此外kk和vv的维度并没有像上面分析的做出区分，而是统一取64，所以vv相对xx确实压缩了维度，但vv与kk的区别似乎不明确。最后的拼接投影，相当于不同头结果进行了一次混合，同时投影回到输入维度。

QKV投影、关联度评分、注意力权重等等，注意力机制看起来比RNN、CNN繁琐不少，但单就获取长程关联这点而言，相比RNN、CNN而言却是更为简单了。RNN获取长程关联必须逐个输入序列的元素，并通过记忆机制保持长程信息；CNN获取更宽的视野同样需要层层卷积，逐级扩展视野范围。而注意力机制则直接从全局出发获取相互关联，同时由于不具有时序依赖，可轻松实现并行计算。

最后，虽然QKV诠释借鉴数据检索的概念，为注意力提供了相对直观的类比，但这其实只是我们的期望，或者说方便理解的角色设定，实际上 Q, K, V 三个嵌入可以是任何我们无从理解的内容，没人知道神经网络的黑盒子在干什么，但无论如何通过引入QKV向量提供了模型必要的灵活性，计算负担可控，而且效果不错。

计算方式

QKV诠释中，投影得到Query向量和Key向量后，关联度评分的计算依然有多种选择：

  • 内积(dot-product)：qTkq^T k (Luong et al. 2015)
  • 缩放内积(scaled dot-product)：qTkdk\small\displaystyle \frac{q^T k}{\sqrt{d_k}} (Vaswani et al. 2017)
  • 加法(additive)：uTf(q+k)u^T f(q + k) (Bahdanau et al. 2014)
  • 局部(location-based)：a(k,q)=a(q)a(k,q) = a(q) (Luong et al. 2015)
  • 相似度：采用常见的相似性测度，如余弦相似度 sim(k,q){\rm sim}(k,q) (Graves et al. 2014)

注1：Vaswani等人在Transformer中对比了加法注意力和内积注意力，发现在Key向量的维度较小时，模型效果差别不大。而随着Key向量的维度增加，使用加法注意力的模型表现要更高。作者猜测是因为随着Key的维度增加，某些向量间关联评分将被放大，softmax归一化时，函数会趋于饱和，影响梯度传递。假设q,kq, k向量元素值为均值0，方差1的独立随机变量，则qTk=∑iqi,kiq^Tk = \sum_i q_i,k_i将是均值0，方差dkd_k的随机变量。为抵消该效应，作者引入了额外的缩放因子dk\sqrt{d_k}。

注2：虽然很多地方(包括不少综述)都会同时介绍加法(additive)和拼接(concat)两种算法，但其实后者包含前者，Luong文中引入拼接算法就是用于指代Bahdanau的加法算法。矩阵以特定方式拼接后相乘可以得到矩阵相乘相加相同结果：矩阵相乘结果维度行数决定于左侧矩阵、列数决定于右侧矩阵，两组矩阵分别相乘后可以相加，要求位于左侧矩阵行数相同，位于右侧矩阵列数相同，从而可分别将两组矩阵左侧逐行拼接、右侧逐列拼接后再相乘，最终结果与相乘相加一致。具体到上面注意力的计算，退回投影得到q和k向量之前，加法注意力uTf(Wqxq+Wkxk)\small u^T f(W_q x_q + W_k x_k)，其中加法操作要求Wq,Wk\small W_q, W_k的行数相同，只需将两者横向拼接，同时向量xk,xqx_k, x_q纵向拼接，再相乘即可，uTf(W[xq;xk])u^T f(W[x_q;x_k])。

注3：余弦相似度算法，有些地方也称之为基于内容的(content-based)注意力。名称源自首次使用该计算方式的文章中提出了两种借助注意力的内存寻址方式：基于内容的(content-based)和基于地址的(location-based)，两者可配合使用。基于内容的类似此处讨论的注意力机制，通过对比检索关键字与数据内容得到注意力权重；基于地址的则是由当前各位置的注意力权重及地址偏移量(索引差值)更新(rotate)地址的注意力权重，具体可参考这篇文章。脱离原文语境，尤其是在QKV诠释下，再使用这个名字是完全不合适的，因为通常讲的注意力机制本质都是基于内容的注意力。

从最初基于RNN隐状态，利用神经网络计算的注意力(Bahdanau et al. 2014)，到更为简单的内积注意力(Luong et al. 2015)，再到完全摆脱RNN的自注意力(Vaswani et al. 2017)，注意力在演化过程中逐渐变得更为简单，也更反映其本质：

  • 从机器翻译角度，编码器与解码器之间的注意力其实是一种对齐机制；
  • 从加权求和角度，注意力是基于关注目标对于输入信息的选择性抽取；
  • 从数据表示角度，注意力是将任意数据集表示压缩至与目标对应大小；

这篇文章还提到一种基于无向图的视角：将输入对应为所有节点间都相互连接的带权无向图，注意力加权就基于连接权重整合所有节点内容，每次自注意力操作会对所有节点同步(并行)执行该操作，用整合后向量替换当前节点向量，得到一个全新的图。如果独立创建多个新的图就是多头注意力(最后将各个图对应节点混合作为最终表示)，而如果反复重复上述无向图的更新操作，则对应于多层注意力。在这一视角下，注意力机制某种程度上跟霍普菲尔德(Hopfield)网络有点像，不过权重规则不同，节点与自身也有连接，且状态更新也不追求稳态，而是作为神经网络整体的一部分，与网络协同收敛。

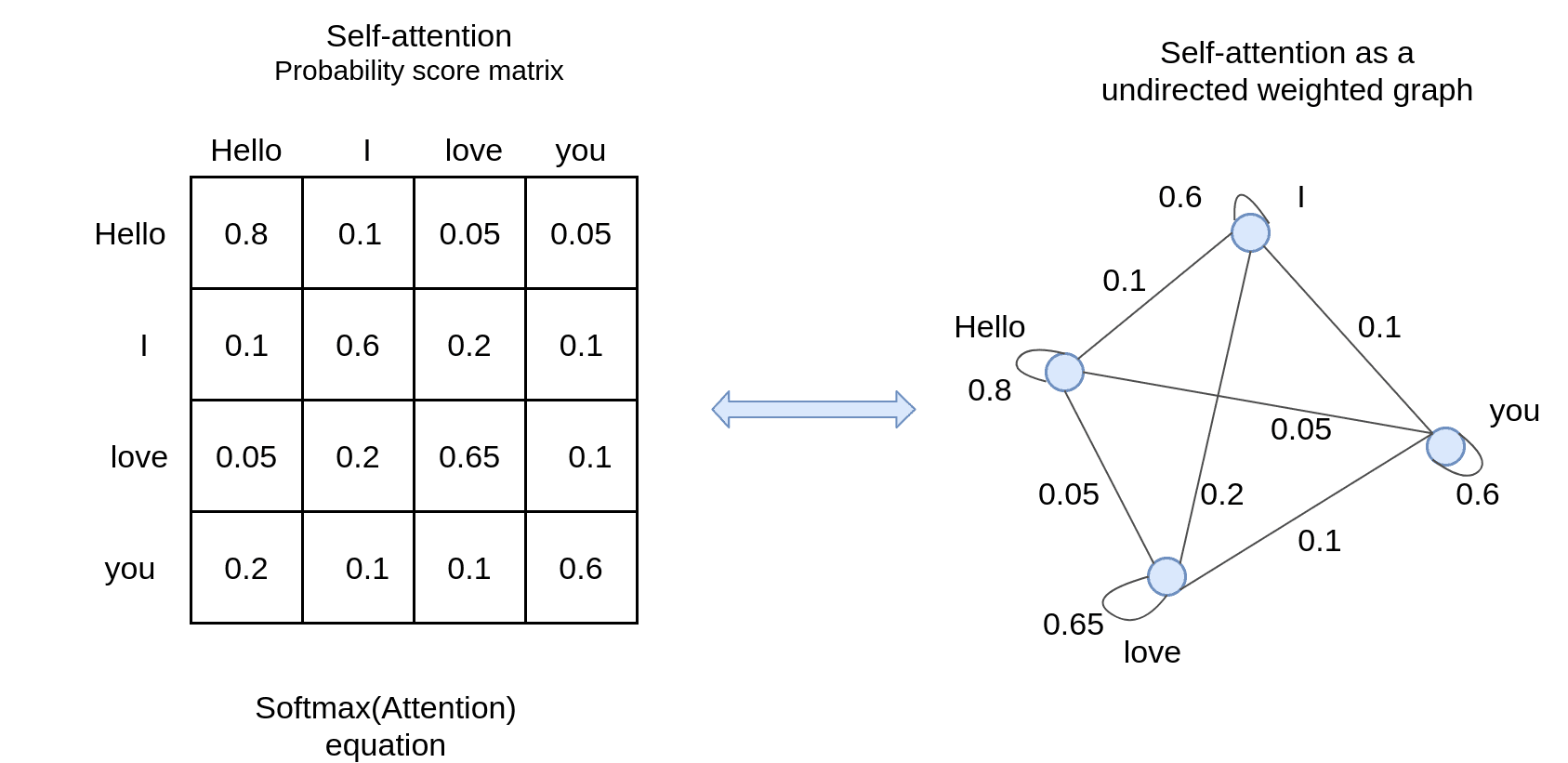
Self-attention as a graph (source: Nikolas Adaloglou)

对比分析

CNN中是从局部特征开始逐级构建顶层特征，且具有某种程度的平移不变性；RNN则更强调时序结构，同样由局部开始抽取特征(序列由短到长)。自注意力机制则完全没有结构上的先验信息(预设)，直接抽取全局特征。这种归纳偏置(Inductive Bias)的减少，赋予模型更多灵活性的同时，也使得模型在小数集上更容易过拟合，因此Transformer/自注意力更多用于大规模预训练模型。此外，自注意力机制是位置无关的，在用于实际任务时通常需要额外引入位置编码。

如果跳出计算的细节，自注意力机制乍一看其实跟全连接很像，所有的输入连接到所有输出，这也是最初困扰我的地方。两者区别在于具体的连接方式：在全连接中连接权重wijw_{ij}不依赖于任何输入，为模型自由参数，同时输出长度任意(权重矩阵维度随之变化)；自注意力机制中，连接权重aija_{ij}(attention weight)依赖于输入，由输入两两相互关联得到，且输出维度始终与输入长度保持一致。此外，注意力机制中看似输出是输入的线性组合(加权求和)，但由于权重同样是非线性依赖输入的，因此这里其实还是非线性的变换，而全连接中则需要额外的非线性激活函数。不过注意力机制的非线性是有限的，因此通常会与MLP配合使用，对每个输出“独立”进行非线性变换。

而对比不同网络实现，还会注意到权重共享是所有非全连接结构的共同要点。全连接中所有输入连接所有输出，参数量决定于输入输出维度；CNN中输入维度为图片像素数，参数量却仅取决于卷积核维度(及通道数)，所有输入共享权重；RNN中输入维度为词向量维度，参数量由词向量(输入)及隐状态(输入/输出)维度决定，所有词向量共享权重；注意力机制中，输入维度为词向量维度×序列长度，所有词向量共享投影权重Wq,Wk,WvW_q, W_k, W_v。

如果将RNN的输入看做依次的单个单词，与之对应的全连接也可以实现词向量间的权重共享，典型的例子就是word2vec词嵌入。但实际上，RNN的输入是整个语句序列，这点在展开形式下更好理解，每个循环模块展开对应一层网络，深层网络需要叠加多个循环结构。在注意力机制下这一切更为显然，所有序列单词必须批量提供(用以分配注意力权重)，而不能逐个输入，与之对应的全连接是无法在序列词语间共享权重的。也正因如此全连接无法适应输入序列长度的变化，而RNN和注意力机制则不存在这样的限制。

应用扩展

常见名词

  • 互注意力(cross attention)：跨越数据集的注意力分配，关注的目标源自关注的内容之外，早期也称相互注意力(inter-attention)。cross没有统一的翻译，常见有互注意力、交叉注意力或者跨越注意力。在Seq2Seq中，也被称为编解码器注意力(encoder-decoder attention)。
  • 自注意力(self attention)：基于数据集自身的注意力分配，即关注的目标出自内容本身，早期也称内部注意力(intra-attention)。在Seq2Seq中，也被称为编码器注意力(encoder-only attention)及解码器注意力(decoder-only attention)。
  • 注意力(attention)：单独的注意力可作为互注意力和自注意力的统称，有时候也会特指互注意力，而自注意力则通常会明确指出。
  • 多头注意力(multi-head attention)：多头类似多个人同时读一本书，每个人可能注意到不同要点，综合在一起获得更全面理解，与CNN中多个卷积核(通道)思想一脉相承。而且类似于集成学习，理论上可减少参数随机初始化的影响，提升模型稳定性，避免单头的“偏见”。此外，Transformer的作者还提到注意力的全局加权求和一定程度上会降低模型的细节分辨力，而多头注意力有助于应对该问题(at the cost of reduced effective resolution due to averaging attention-weighted positions, an effect we counteract with Multi-Head Attention)。在Transformer中不同头的注意力被拼接在一起，之后整体进行了一次投影作为最终输出，相当于对多头进行混合，并投影回输入维度(便于接入残差连接)。
  • 多层注意力(multi-layer attention)：多层注意力相当于阅读多遍，且不同于多头注意力独立阅读原文，多层注意力每次阅读之前“重写”的内容，层层堆叠。预期效果是从词向量开始，逐级整合，提取更高级的文本特征，如短语、从句结构、段落结构等。需要注意的是，注意力层通常不是直接堆叠，而是会与普通神经网络层穿插：如层次注意力中注意力层之间有双向RNN，Transformer中自注意力层后有MLP。
  • 硬注意力(hard attention)：相比关注全部输入的软/全局注意力，硬注意力随机挑选离散的样本用于上下文向量计算，缺点在于不可微。
  • 局部注意力(local attention)：相比关注全部输入的软/全局注意力，局部注意力挑选连续的局部样本(窗口)用于上下文向量计算，难点在于窗口中心位置的合理选取。

更多注意力机制变种术语可参考Papers with Code的列表。

具体应用

  • 可微硬件 NTM(Neural Turing Machines), DNC(Differentiable Neural Computer)
    虽然RNN被证明是图灵完备的，但将其扩展为计算机却并不简单，这其中最困难的是如何实现“可微分”的存储管理，以便于整个系统的训练学习。NTM参考注意力机制提出了一种全新的内存访问方式：每次系统都访问全部内存，并根据内容分配不同的读/写权重，即将传统电脑的硬注意力替换为软注意力。基于这种完全可微的内存访问机制为基础，NTM建立了全新的以神经网络为中心的计算系统。不过这其中内存访问速度(注意力计算)随内存增加是线性增加的，如何提升速度是改进关键。
  • 指针网络 Ptr-Net(Pointer Network)
    组合类优化问题中输出就是输入的子集或重排，如最短路径或序列排序。状态是完全离散的，不同状态间不存在“相似”的概念，NLP中连续的分布式表示(Embedding)不再适用。使用注意力机制处理这类问题时，不能对输入进行融合(加权求和)，而是直接根据注意力权重指向特定输入元素(指针)。
  • 自适应运算时间 ACT(Adaptive Computation Time)
    普通RNN每次循环(time step)执行相同计算量(和时间)。在自适应运算时间中，每次循环会由RNN自主决定算几步，具体步数使用注意力机制确定，以保证可微。每步计算会根据结果分配一个注意力权重，总权重取为1，当各步权重和接近1时中止计算，将所有中间步结果加权求和作为最终输出，并转入后续循环。
  • 层级注意力 HAN(Hierarchical Attention Network)
    词向量(RNN+Attn) → 句向量(RNN+Attn)：对句子内词语应用双向RNN+注意力，之后在输出的句向量之间再次应用双向RNN+注意力。注意力计算有点怪，类似局部注意力，uTtanh⁡(Wx+b)u^T\tanh(Wx+b)，u,Wu, W为参数。
  • 注意力增强卷积
    • 图像处理：Show, Attend and Tell、ABC-CNN(Attention-Based Configurable CNN)、SENet(Squeeze-and-Excitation Network)、AA-ResNet(Attention Augmented ConvNet)
      用于特征图、用于卷积通道(对通道加权)、注意力结果与卷积结果拼接…
    • 序列处理：ABCNN(Attention-Based CNN)、ConvS2S(Convolutional Seq2Seq)
      卷积前引入注意力、卷积后引入注意力、基于注意力实现池化…
    • 元学习/强化学习：SNAIL(Simple Neural Attentive Learner)
      将单侧自注意力与单侧卷积(时序卷积/因果卷积)结合，改善自注意力时序无关的缺点，并应用于强化学习。
    • 生成对抗：SAGAN(Self-Attention GAN)
  • 注意力替代卷积
    • Ramachandran et al. 2019：Stand-Alone Self-Attention in Vision Models
    • Cordonnier et al. 2019：Self-Attention v.s. Convolutional Layers
      文章证明只要头够多，多头自注意力表示能力要优于卷积(至少不会更差)。

      We showed that self-attention layers applied to images can express any convolutional layer (given sufficiently many heads) and that fully-attentional models learn to combine local behavior (similar to convolution) and global attention based on input content. More generally, fully-attentional models seem to learn a generalization of CNNs where the kernel pattern is learned at the same time as the filters — similar to deformable convolutions.

    • Dosovitskiy et al. 2020：Vision Transformer, ViT
      最初的尝试是直接将注意力应用于像素点，计算量会很大(像素数平方量级)，通常需要对图片进行下采样，或者参照卷积操作，将注意力应用范围限制在当前像素周围的小窗口。前者显然存在信息损失，而后者则削弱了注意力直接提取全局关联性的优势。因此效果上只算是可用，而无法超越CNN，直至ViT出现。ViT对图片切分后应用注意力，获得了超越当时领先CNN模型的表现，具体将在Transformer部分介绍。

扩展阅读
机器翻译简史：八十多年来，人类就是要再造一座通天塔
什么是transformer？ - KnowingAI知智
Self-attention step-by-step - Peltarion
An Attentive Survey of Attention Models
A Review on the Attention Mechanism of Deep Learning
Attention and Memory in Deep Learning - DeepMindxUCL
Attention and Augmented Recurrent Neural Networks
Neural Machine Translation (seq2seq) Tutorial