Deep Denerative Model(DGM)生成模型 - 花书 深度生成模型 - 机器之心 Stanford CS236 Cornell CS6785
概率生成模型概述
生成模型简介
生成与判别
贝叶斯法则将生成模型与判别模型联系起来。
生成模型分类 p ( x ) p(x) p ( x )
非深度学习方法:
贝叶斯网络(有向图):朴素贝叶斯、隐马尔科夫链、高斯混合模型(EM算法)
马尔科夫随机场(无向图):(受限)玻尔兹曼机、最大熵
显式密度估计:J = − E x ∼ p data log p model ( x ) \boxed{\mathcal{J} = -\mathbb{E}_{\bm{x}\sim p_\text{data}} \log p_\text{model}(\bm{x})} J = − E x ∼ p data log p model ( x )
优化似然函数:标准化流NF、自回归模型AR、基于能量的模型EBMs
优化证据下界:变分自编码VAE、扩散概率模型DPM、基于得分的模型SBMs
隐式密度估计:
注意,这些类别并不全面,也并非互斥,同一模型同时属于GAN和VAE。事实上,深度生成模型作为一个快速发展的领域,尚不存在统一的理论或视角。
核心目标对比
标准化流 NF:p model ( x ) = q ( g − 1 ( x ; θ ) ) ∣ det J g θ ( z ) ∣ − 1 p_\text{model}(\bm{x}) = q\left(g^{-1}(\bm{x}; \bm{\theta})\right)\left|\det J_{g_\theta}(\bm{z})\right|^{-1} p model ( x ) = q ( g − 1 ( x ; θ ) ) ∣ det J g θ ( z ) ∣ − 1
J = − E x ∼ p data [ log q ( g − 1 ( x ; θ ) ) − log ∣ det J g θ ( z ) ∣ ] \mathcal{J} = -\mathbb{E}_{\bm{x}\sim p_\text{data}} \left[ \log q\left(g^{-1}(\bm{x}; \bm{\theta})\right) - \log\left|\det J_{g_\theta}(\bm{z})\right| \right]
J = − E x ∼ p data [ log q ( g − 1 ( x ; θ ) ) − log ∣ det J g θ ( z ) ∣ ]
p model ( x ) = q ( f ( x ; θ ) ) ∣ det J f θ ( z ) ∣ p_\text{model}(\bm{x}) = q\left(f(\bm{x}; \bm{\theta})\right)\left|\det J_{f_\theta}(\bm{z})\right|
p model ( x ) = q ( f ( x ; θ ) ) ∣ det J f θ ( z ) ∣
J = − E x ∼ p data [ log q ( f ( x ; θ ) ) + log ∣ det J f θ ( z ) ∣ ] \mathcal{J} = -\mathbb{E}_{\bm{x}\sim p_\text{data}} \left[ \log q\left(f(\bm{x}; \bm{\theta})\right) + \log\left|\det J_{f_\theta}(\bm{z})\right| \right]
J = − E x ∼ p data [ log q ( f ( x ; θ ) ) + log ∣ det J f θ ( z ) ∣ ]
自回归模型 AR:p model ( x ) = ∏ i = 1 n p ( x i ∣ x < i ; θ ) p_\text{model}(\bm{x}) = \prod_{i=1}^n p(x_i|x_{<i};\theta) p model ( x ) = ∏ i = 1 n p ( x i ∣ x < i ; θ ) 变分自编码 VAE:p model ( x ) = ∫ q ( z ) p ( x ∣ z ; θ ) d z p_\text{model}(x) = \int q(z) p(x|z; \theta) dz p model ( x ) = ∫ q ( z ) p ( x ∣ z ; θ ) d z
p ( x ; θ ) = ∫ q ( z ) p ( x , z ; θ ) q ( z ) d z = E x ∼ q ( z ) p ( x , z ; θ ) q ( z ) p(x; \theta) = \int q(z) \frac{p(x, z; \theta)}{q(z)} dz = \mathbb{E}_{\bm{x}\sim q(z)} \frac{p(x, z; \theta)}{q(z)}
p ( x ; θ ) = ∫ q ( z ) q ( z ) p ( x , z ; θ ) d z = E x ∼ q ( z ) q ( z ) p ( x , z ; θ )
p ( x ; θ , ϕ ) = ∫ q ( z ∣ x ; ϕ ) p ( x , z ; θ ) q ( z ∣ x ; ϕ ) d z = E x ∼ q ( z ∣ x ; ϕ ) p ( x , z ; θ ) q ( z ∣ x ; ϕ ) p(x; \theta,\phi) = \int q(z|x;\phi) \frac{p(x, z; \theta)}{q(z|x;\phi)} dz = \mathbb{E}_{\bm{x}\sim q(z|x;\phi)} \frac{p(x, z; \theta)}{q(z|x;\phi)}
p ( x ; θ , ϕ ) = ∫ q ( z ∣ x ; ϕ ) q ( z ∣ x ; ϕ ) p ( x , z ; θ ) d z = E x ∼ q ( z ∣ x ; ϕ ) q ( z ∣ x ; ϕ ) p ( x , z ; θ )
log p ( x ; θ , ϕ ) = log E x ∼ q ( z ∣ x ; ϕ ) p ( x , z ; θ ) q ( z ∣ x ; ϕ ) ≥ E x ∼ q ( z ∣ x ; ϕ ) log p ( x , z ; θ ) q ( z ∣ x ; ϕ ) \log p(x; \theta,\phi) =\log \mathbb{E}_{\bm{x}\sim q(z|x;\phi)} \frac{p(x, z; \theta)}{q(z|x;\phi)} \ge \mathbb{E}_{\bm{x}\sim q(z|x;\phi)} \log \frac{p(x, z; \theta)}{q(z|x;\phi)}
log p ( x ; θ , ϕ ) = log E x ∼ q ( z ∣ x ; ϕ ) q ( z ∣ x ; ϕ ) p ( x , z ; θ ) ≥ E x ∼ q ( z ∣ x ; ϕ ) log q ( z ∣ x ; ϕ ) p ( x , z ; θ )
J ( θ , ϕ ) = E x ∼ p data [ D KL ( q ( z ∣ x ; ϕ ) ∥ q ( z ) ) − E z ∼ q ( z ∣ x ; ϕ ) log p ( x ∣ z ; θ ) ] \boxed{\mathcal{J}(\bm{\theta}, \bm{\phi}) = \mathbb{E}_{\bm{x}\sim p_\text{data}} \left[ D_\text{KL}\big( q(\bm{z}|\bm{x}; \bm{\phi}) \| q(\bm{z}) \big) - \mathbb{E}_{z\sim q(\bm{z}|\bm{x}; \bm{\phi})} \log p(\bm{x}|\bm{z}; \bm{\theta})\right] }
J ( θ , ϕ ) = E x ∼ p data [ D KL ( q ( z ∣ x ; ϕ ) ∥ q ( z ) ) − E z ∼ q ( z ∣ x ; ϕ ) log p ( x ∣ z ; θ ) ]
基于能量的模型 EBMs p model ( x ) = 1 Z ( θ ) e − E ( x ; θ ) p_\text{model}(x) = \frac{1}{Z(\theta)} e^{-E(x; \theta)} p model ( x ) = Z ( θ ) 1 e − E ( x ; θ ) E ( x ; θ ) E(x; \theta) E ( x ; θ ) E ( x ; θ ) E(x; \theta) E ( x ; θ ) J ( θ ) = − E x ∼ p data ( x ) log p model ( x ) = E x ∼ p data ( x ) E ( x ; θ ) + log Z ( θ ) \mathcal{J}(\theta) = -\mathbb{E}_{x \sim p_\text{data}(x)} \log p_\text{model}(x) = \mathbb{E}_{x \sim p_\text{data}(x)} E(x;\theta) + \log Z(\theta)
J ( θ ) = − E x ∼ p data ( x ) log p model ( x ) = E x ∼ p data ( x ) E ( x ; θ ) + log Z ( θ )
其中Z ( θ ) Z(\theta) Z ( θ ) ∇ θ J ( θ ) = E x ∼ p data ( x ) ∇ θ E ( x ; θ ) − E x ∼ p ( x ; θ ) ∇ θ E ( x ; θ ) \boxed{\nabla_{\theta} \mathcal{J}(\theta) = \mathbb{E}_{x \sim p_\text{data}(x)} \nabla_{\theta} E(x;\theta) - \mathbb{E}_{x \sim p(x; \theta)} \nabla_{\theta} E(x;\theta)}
∇ θ J ( θ ) = E x ∼ p data ( x ) ∇ θ E ( x ; θ ) − E x ∼ p ( x ; θ ) ∇ θ E ( x ; θ )
后一项需要对p ( x ; θ ) p(x; \theta) p ( x ; θ ) 基于得分的模型 SBMs:p model ( x ) → ∇ x log p model ( x ) p_\text{model}(x) \rightarrow \nabla_x \log p_\text{model}(x) p model ( x ) → ∇ x log p model ( x ) J ( θ ) = − E x ∼ p data ( x ) [ ∥ ∇ x log p ( x ; θ ) ∥ 2 + 1 2 t r ( ∇ x 2 log p ( x ; θ ) ) ] \boxed{\mathcal{J}(\theta) = -\mathbb{E}_{x \sim p_\text{data}(x)} \left[ \| \nabla_{x} \log p(x; \theta) \|^2 +\frac{1}{2} {\rm tr}\big(\nabla_{x}^2 \log p(x;\theta)\big) \right]}
J ( θ ) = − E x ∼ p data ( x ) [ ∥ ∇ x log p ( x ; θ ) ∥ 2 + 2 1 t r ( ∇ x 2 log p ( x ; θ ) ) ]
L = E x 0 ∼ q ( x 0 ) , ϵ ∼ N ( 0 , I ) ∥ ϵ − ϵ ~ ( x t ( x 0 , ϵ ) , t ; θ ) ∥ 2 \boxed{L = \mathbb{E}_{x_0 \sim q(x_0), \epsilon\sim\tiny \mathcal{N}(0,I)} \left\|\epsilon - \tilde{\epsilon}\big(x_t(x_0, \epsilon), t; \bm{\theta}\big)\right\|^2 }
L = E x 0 ∼ q ( x 0 ) , ϵ ∼ N ( 0 , I ) ∥ ∥ ∥ ϵ − ϵ ~ ( x t ( x 0 , ϵ ) , t ; θ ) ∥ ∥ ∥ 2
生成对抗网络 GANarg min θ arg max ϕ J ( G ( z ; θ ) , D ( x ; ϕ ) ) \argmin_\bm{\theta} \argmax_\bm{\phi} \mathcal{J}\Big(G(z; \bm{\theta}), D(x; \bm{\phi})\Big)
θ a r g m i n ϕ a r g m a x J ( G ( z ; θ ) , D ( x ; ϕ ) )
GAN由生成器和判别器组成,基本思路是生成器产生模拟样本x ( G ) = G ( z ; θ ) x^{(G)} = G(z; \bm{\theta}) x ( G ) = G ( z ; θ ) D D D J ( θ , ϕ ) = E x ∼ p data log D ( x ; ϕ ) − E x ( G ) ∼ p g ( x ∣ z ; θ ) log D ( x ( G ) ; ϕ ) J ( θ , ϕ ) = E x ∼ p data D ( x ; ϕ ) − E x ( G ) ∼ p g ( x ∣ z ; θ ) D ( x ( G ) ; ϕ ) , ∥ D ∥ L ≤ 1 \begin{aligned}
\mathcal{J}(\bm{\theta}, \bm{\phi}) =& \mathbb{E}_{\bm{x}\sim p_\text{data}} \log D(\bm{x};\bm{\phi}) - \mathbb{E}_{\bm{x}^{(G)}\sim p_\text{g}(\bm{x} | \bm{z}; \bm{\theta})} \log D\big( \bm{x}^{(G)}; \bm{\phi} \big)\\
\mathcal{J}(\bm{\theta}, \bm{\phi}) =& \mathbb{E}_{\bm{x}\sim p_\text{data}} D(\bm{x};\bm{\phi}) - \mathbb{E}_{\bm{x}^{(G)} \sim p_\text{g}(\bm{x}|\bm{z};\bm{\theta})} D(\bm{x}^{(G)};\bm{\phi}), \small \|D\|_L\le 1
\end{aligned} J ( θ , ϕ ) = J ( θ , ϕ ) = E x ∼ p data log D ( x ; ϕ ) − E x ( G ) ∼ p g ( x ∣ z ; θ ) log D ( x ( G ) ; ϕ ) E x ∼ p data D ( x ; ϕ ) − E x ( G ) ∼ p g ( x ∣ z ; θ ) D ( x ( G ) ; ϕ ) , ∥ D ∥ L ≤ 1
主要参考花书P592 #20.10.2章节内容
目前生成模型的主流是可微生成网络,核心思路是通过可微函数g ( z ; θ ) g(\bm{z}; \bm{\theta}) g ( z ; θ ) z \bm{z} z x \bm{x} x
这里简单分析变换对概率分布的影响,设x = g ( z ) x = g(z) x = g ( z ) g g g x , z x, z x , z p ( x ) , q ( z ) p(x), q(z) p ( x ) , q ( z ) p ( x ) ∣ d x ∣ = q ( z ) ∣ d z ∣ p(x)|dx| = q(z)|dz| p ( x ) ∣ d x ∣ = q ( z ) ∣ d z ∣ d x , d z dx, dz d x , d z q ( z ) = p ( x ) ∣ d x d z ∣ q(z) = p(x)|\frac{dx}{dz}| q ( z ) = p ( x ) ∣ d z d x ∣
q ( z ) = p ( x ( z ) ) ∣ det ( ∂ x ∂ z ) ∣ = p ( g ( z ) ) ∣ det ( ∂ g ( z ) ∂ z ) ∣ q(\bm{z}) = p(\bm{x}(\bm{z})) \left|\det\left(\frac{\partial\bm{x}}{\partial\bm{z}}\right)\right| = p\left(g(\bm{z})\right) \left|\det\left(\frac{\partial g(\bm{z})}{\partial\bm{z}}\right)\right|
q ( z ) = p ( x ( z ) ) ∣ ∣ ∣ ∣ ∣ det ( ∂ z ∂ x ) ∣ ∣ ∣ ∣ ∣ = p ( g ( z ) ) ∣ ∣ ∣ ∣ ∣ det ( ∂ z ∂ g ( z ) ) ∣ ∣ ∣ ∣ ∣
反过来有:
p ( x ) = q ( g − 1 ( x ) ) ∣ det ( ∂ g ( z ) ∂ z ) ∣ − 1 p(\bm{x}) = q\left(g^{-1}(\bm{x})\right) \left|\det\left(\frac{\partial g(\bm{z})}{\partial\bm{z}}\right)\right|^{-1}
p ( x ) = q ( g − 1 ( x ) ) ∣ ∣ ∣ ∣ ∣ det ( ∂ z ∂ g ( z ) ) ∣ ∣ ∣ ∣ ∣ − 1
事实上,直接获得p ( x ) p(\bm{x}) p ( x ) p ( x ∣ z ) p(\bm{x}|\bm{z}) p ( x ∣ z ) x \bm{x} x
p ( x ) = ∫ p ( x ∣ z ) q ( z ) d z = E z ∼ q ( z ) p ( x ∣ z ) p(\bm{x}) = \int p(\bm{x}|\bm{z})q(\bm{z})d\bm{z} = \mathbb{E}_{\bm{z}\sim q(\bm{z})} p(\bm{x}|\bm{z})
p ( x ) = ∫ p ( x ∣ z ) q ( z ) d z = E z ∼ q ( z ) p ( x ∣ z )
为得到上述可对隐变量z \bm{z} z q ( z ) q(\bm{z}) q ( z ) N ( 0 , I ) \mathcal{N}(0, I) N ( 0 , I ) p ( x ∣ z ) ∼ 0 p(\bm{x}|\bm{z}) \sim 0 p ( x ∣ z ) ∼ 0 q ( z ∣ x ) p ( x ) = p ( x ∣ z ) q ( z ) q(z|x)p(x) = p(x|z)q(z) q ( z ∣ x ) p ( x ) = p ( x ∣ z ) q ( z )
p ( x ) = p ( x ∣ z ) q ( z ) q ( z ∣ x ) p(x) = \frac{p(x|z)q(z)}{q(z|x)}
p ( x ) = q ( z ∣ x ) p ( x ∣ z ) q ( z )
其中q ( z ∣ x ) , p ( x ∣ z ) q(z|x), p(x|z) q ( z ∣ x ) , p ( x ∣ z )
前一策略的代表为基于流的模型及扩散模型,后一策略的代表有变分自编码和对抗生成网络。
重参数化技巧
主要参考花书P586 #20.9章节内容
随机采样的反向传递Auto-Encoding Variational Bayes Stochastic Backpropagation and Approximate Inference in Deep Generative Models
变分自编码器VAE
https://en.wikipedia.org/wiki/Variational_autoencoder Auto-Encoding Variational Bayes Tutorial on Variational Autoencoders 2016
VAE公式推导一般是从D K L ( q ( z ∣ x ; ϕ ) ∥ q ( z ∣ x ; θ ) ) D_{\rm KL}\big( q(\bm{z}|\bm{x};\bm{\phi}) \big\| q(\bm{z}|\bm{x};\bm{\theta})\big) D K L ( q ( z ∣ x ; ϕ ) ∥ ∥ ∥ q ( z ∣ x ; θ ) ) z \bm{z} z g ( z ; θ ) g(\bm{z};\bm{\theta}) g ( z ; θ ) p ( x ∣ z ; θ ) p(\bm{x}|\bm{z};\bm{\theta}) p ( x ∣ z ; θ ) x \bm{x} x q ( z ∣ x ) p ( x ) = p ( x ∣ z ) q ( z ) q(z|x)p(x) = p(x|z)q(z) q ( z ∣ x ) p ( x ) = p ( x ∣ z ) q ( z )
p ( x ) = p ( x ∣ z ; θ ) q ( z ) q ( z ∣ x ; θ ) p(\bm{x}) = \frac{p(\bm{x}|\bm{z}; \bm{\theta})q(\bm{z})}{q(\bm{z}|\bm{x}; \bm{\theta})}
p ( x ) = q ( z ∣ x ; θ ) p ( x ∣ z ; θ ) q ( z )
这其中q ( z ) q(\bm{z}) q ( z ) z \bm{z} z N ( 0 , I ) \mathcal{N}(0, I) N ( 0 , I ) p ( x ∣ z ; θ ) p(\bm{x}|\bm{z}; \bm{\theta}) p ( x ∣ z ; θ ) z \bm{z} z x \bm{x} x q ( z ∣ x ; θ ) q(\bm{z}|\bm{x}; \bm{\theta}) q ( z ∣ x ; θ ) G ( z ; θ ) G(\bm{z};\bm{\theta}) G ( z ; θ ) x \bm{x} x z \bm{z} z E ( x ; ϕ ) E(\bm{x}; \bm{\phi}) E ( x ; ϕ ) q ( z ∣ x ; θ ) q(\bm{z}|\bm{x}; \bm{\theta}) q ( z ∣ x ; θ )
p ( x ) = p ( x ∣ z ; θ ) q ( z ) q ( z ∣ x ; ϕ ) q ( z ∣ x ; ϕ ) q ( z ∣ x ; θ ) p(\bm{x}) = \frac{p(\bm{x}|\bm{z}; \bm{\theta})q(\bm{z})}{q(\bm{z}|\bm{x}; \bm{\phi})} \frac{q(\bm{z}|\bm{x}; \bm{\phi})}{q(\bm{z}|\bm{x}; \bm{\theta})}
p ( x ) = q ( z ∣ x ; ϕ ) p ( x ∣ z ; θ ) q ( z ) q ( z ∣ x ; θ ) q ( z ∣ x ; ϕ )
由于q ( z ∣ x ; θ ) q(\bm{z}|\bm{x}; \bm{\theta}) q ( z ∣ x ; θ ) z ∼ q ( z ∣ x ; ϕ ) \bm{z}\sim q(\bm{z}|\bm{x}; \bm{\phi}) z ∼ q ( z ∣ x ; ϕ )
log p ( x ) = E z ∼ q ( z ∣ x ; ϕ ) [ log p ( x ∣ z ; θ ) − log q ( z ∣ x ; ϕ ) q ( z ) + log q ( z ∣ x ; ϕ ) q ( z ∣ x ; θ ) ] = E z ∼ q ( z ∣ x ; ϕ ) log p ( x ∣ z ; θ ) − D KL ( q ( z ∣ x ; ϕ ) ∥ q ( z ) ) + D KL ( q ( z ∣ x ; ϕ ) ∥ q ( z ∣ x ; θ ) ) \begin{aligned}
\log p(\bm{x}) =& \mathbb{E}_{z\sim q(\bm{z}|\bm{x}; \bm{\phi})} \left[\log p(\bm{x}|\bm{z}; \bm{\theta}) - \log \frac{q(\bm{z}|\bm{x}; \bm{\phi})}{q(\bm{z})} + \log\frac{q(\bm{z}|\bm{x}; \bm{\phi})}{q(\bm{z}|\bm{x}; \bm{\theta})}\right]\\
=& \mathbb{E}_{z\sim q(\bm{z}|\bm{x}; \bm{\phi})} \log p(\bm{x}|\bm{z}; \bm{\theta}) - D_\text{KL}\big( q(\bm{z}|\bm{x}; \bm{\phi}) \| q(\bm{z}) \big) \\
&~~ + D_\text{KL}\big(q(\bm{z}|\bm{x}; \bm{\phi}) \| q(\bm{z}|\bm{x}; \bm{\theta}) \big)
\end{aligned} log p ( x ) = = E z ∼ q ( z ∣ x ; ϕ ) [ log p ( x ∣ z ; θ ) − log q ( z ) q ( z ∣ x ; ϕ ) + log q ( z ∣ x ; θ ) q ( z ∣ x ; ϕ ) ] E z ∼ q ( z ∣ x ; ϕ ) log p ( x ∣ z ; θ ) − D KL ( q ( z ∣ x ; ϕ ) ∥ q ( z ) ) + D KL ( q ( z ∣ x ; ϕ ) ∥ q ( z ∣ x ; θ ) )
这其中D KL ( q ( z ∣ x ; ϕ ) ∥ q ( z ∣ x ; θ ) ) D_\text{KL}\big(q(\bm{z}|\bm{x}; \bm{\phi}) \| q(\bm{z}|\bm{x}; \bm{\theta}) \big) D KL ( q ( z ∣ x ; ϕ ) ∥ q ( z ∣ x ; θ ) ) − E x ∼ p ^ data log p ( x ) -\mathbb{E}_{\bm{x}\sim \hat{p}_\text{data}} \log p(\bm{x}) − E x ∼ p ^ data log p ( x ) log p ( x ) \log p(\bm{x}) log p ( x )
− log p ( x ) + D KL ( q ( z ∣ x ; ϕ ) ∥ q ( z ∣ x ; θ ) ) = D KL ( q ( z ∣ x ; ϕ ) ∥ q ( z ) ) − E z ∼ q ( z ∣ x ; ϕ ) log p ( x ∣ z ; θ ) \begin{aligned}
-\log p(\bm{x}) + D_\text{KL}\big(q(\bm{z}|\bm{x}; \bm{\phi})& \| q(\bm{z}|\bm{x}; \bm{\theta}) \big) \\
=& D_\text{KL}\big( q(\bm{z}|\bm{x}; \bm{\phi}) \| q(\bm{z}) \big) - \mathbb{E}_{z\sim q(\bm{z}|\bm{x}; \bm{\phi})} \log p(\bm{x}|\bm{z}; \bm{\theta})
\end{aligned} − log p ( x ) + D KL ( q ( z ∣ x ; ϕ ) = ∥ q ( z ∣ x ; θ ) ) D KL ( q ( z ∣ x ; ϕ ) ∥ q ( z ) ) − E z ∼ q ( z ∣ x ; ϕ ) log p ( x ∣ z ; θ )
这里p ( x ) p(\bm{x}) p ( x ) p ( x ∣ θ ) = ∫ p ( x ∣ z ; θ ) q ( z ) d z p(\bm{x}|\bm{\theta}) = \int p(\bm{x}|\bm{z};\bm{\theta})q(\bm{z})d\bm{z} p ( x ∣ θ ) = ∫ p ( x ∣ z ; θ ) q ( z ) d z q ( z ) q(\bm{z}) q ( z ) θ \bm{\theta} θ 证据 。arg max θ p ( x ∣ θ ) \argmax_{\bm{\theta}}p(\bm{x}|\bm{\theta}) a r g m a x θ p ( x ∣ θ ) x \bm{x} x q ( z ) q(\bm{z}) q ( z ) D KL ( q ( z ∣ x ; ϕ ) ∥ q ( z ∣ x ; θ ) ) D_\text{KL}\big(q(\bm{z}|\bm{x}; \bm{\phi}) \| q(\bm{z}|\bm{x}; \bm{\theta}) \big) D KL ( q ( z ∣ x ; ϕ ) ∥ q ( z ∣ x ; θ ) ) log p ( x ) \log p(\bm{x}) log p ( x ) p ( x ) p(\bm{x}) p ( x )
最终,VAE网络整体损失函数为:
J ( θ , ϕ ) = E x ∼ p data [ D KL ( q ( z ∣ x ; ϕ ) ∥ q ( z ) ) − E z ∼ q ( z ∣ x ; ϕ ) log p ( x ∣ z ; θ ) ] \boxed{\mathcal{J}(\bm{\theta}, \bm{\phi}) = \mathbb{E}_{\bm{x}\sim p_\text{data}} \left[ D_\text{KL}\big( q(\bm{z}|\bm{x}; \bm{\phi}) \| q(\bm{z}) \big) - \mathbb{E}_{z\sim q(\bm{z}|\bm{x}; \bm{\phi})} \log p(\bm{x}|\bm{z}; \bm{\theta})\right] }
J ( θ , ϕ ) = E x ∼ p data [ D KL ( q ( z ∣ x ; ϕ ) ∥ q ( z ) ) − E z ∼ q ( z ∣ x ; ϕ ) log p ( x ∣ z ; θ ) ]
实际计算中q ( z ∣ x ; ϕ ) q(\bm{z}|\bm{x}; \bm{\phi}) q ( z ∣ x ; ϕ ) z ∼ N ( μ x ; ϕ , Σ x ; ϕ ) \bm{z}\sim\mathcal{N}(\bm{\mu}_\bm{x;\phi}, \bm{\Sigma}_\bm{x;\phi}) z ∼ N ( μ x ; ϕ , Σ x ; ϕ ) q ( z ) q(\bm{z}) q ( z ) N ( 0 , I ) \mathcal{N}(0, I) N ( 0 , I ) μ x ; ϕ , Σ x ; ϕ \bm{\mu}_\bm{x;\phi}, \bm{\Sigma}_\bm{x;\phi} μ x ; ϕ , Σ x ; ϕ
D K L ( N ( μ x ; ϕ , Σ x ; ϕ ) ∥ N ( 0 , I ) ) = 1 2 [ t r ( Σ x ; ϕ ) + μ x ; ϕ T μ x ; ϕ − k − log det ( Σ x ; ϕ ) ] D_{\rm KL}\Big(\mathcal{N}(\bm{\mu}_\bm{x;\phi}, \bm{\Sigma}_\bm{x;\phi}) \big\| \mathcal{N}(0, I)\Big) = \frac{1}{2} [{\rm tr}(\bm{\Sigma}_\bm{x;\phi}) + \bm{\mu}_\bm{x;\phi}^T\bm{\mu}_\bm{x;\phi} - k - \log\det(\bm{\Sigma}_\bm{x;\phi})]
D K L ( N ( μ x ; ϕ , Σ x ; ϕ ) ∥ ∥ ∥ N ( 0 , I ) ) = 2 1 [ t r ( Σ x ; ϕ ) + μ x ; ϕ T μ x ; ϕ − k − log det ( Σ x ; ϕ ) ]
第二项则相对复杂,需要对编码器输出分布q ( z ∣ x ; ϕ ) q(\bm{z}|\bm{x}; \bm{\phi}) q ( z ∣ x ; ϕ ) z ∼ N ( μ x ; ϕ , Σ x ; ϕ ) \bm{z}\sim\mathcal{N}(\bm{\mu}_\bm{x;\phi}, \bm{\Sigma}_\bm{x;\phi}) z ∼ N ( μ x ; ϕ , Σ x ; ϕ ) ϵ ∼ N ( 0 , I ) \bm{\epsilon}\sim\mathcal{N}(0, I) ϵ ∼ N ( 0 , I ) z = μ x ; ϕ + Σ x ; ϕ ϵ \bm{z}{\small =}\bm{\mu}_\bm{x;\phi}{\small +}\bm{\Sigma}_{\bm{x;\phi}}\bm{\epsilon} z = μ x ; ϕ + Σ x ; ϕ ϵ
J ( θ , ϕ ) = E x ∼ p data [ D KL ( q ( z ∣ x ; ϕ ) ∥ q ( z ) ) − E ϵ ∼ N ( 0 , I ) log p ( x ∣ z = μ ϕ + Σ ϕ ϵ ; θ ) ] \mathcal{J}(\bm{\theta}, \bm{\phi}) = \mathbb{E}_{\bm{x}\sim p_\text{data}} \left[ D_\text{KL}\big( q(\bm{z}|\bm{x}; \bm{\phi}) \| q(\bm{z}) \big) - \mathbb{E}_{\bm{\epsilon} \sim \mathcal{N}(0, I)} \log p(\bm{x}|\bm{z}{\small =}\bm{\mu}_\bm{\phi}{\small +}\bm{\Sigma}_{\bm{\phi}}\bm{\epsilon}; \bm{\theta})\right]
J ( θ , ϕ ) = E x ∼ p data [ D KL ( q ( z ∣ x ; ϕ ) ∥ q ( z ) ) − E ϵ ∼ N ( 0 , I ) log p ( x ∣ z = μ ϕ + Σ ϕ ϵ ; θ ) ]
最后,实际计算中,最简单情况可对隐变量只进行一次采样作为近似:
J ( θ , ϕ ) = E x ∼ p ^ data [ D KL ( q ( z ∣ x ; ϕ ) ∥ q ( z ) ) − log p ( x ∣ z = μ ϕ + Σ ϕ ϵ ; θ ) ∣ ϵ ∼ N ( 0 , I ) ] \boxed{\mathcal{J}(\bm{\theta}, \bm{\phi}) = \mathbb{E}_{\bm{x}\sim \hat{p}_\text{data}} \Big[ D_\text{KL}\big( q(\bm{z}|\bm{x}; \bm{\phi}) \| q(\bm{z}) \big) - \log p(\bm{x}|\bm{z}{\small =}\bm{\mu}_\bm{\phi}{\small +}\bm{\Sigma}_{\bm{\phi}}\bm{\epsilon}; \bm{\theta})|_{\bm{\epsilon} \sim \mathcal{N}(0, I)} \Big] }
J ( θ , ϕ ) = E x ∼ p ^ data [ D KL ( q ( z ∣ x ; ϕ ) ∥ q ( z ) ) − log p ( x ∣ z = μ ϕ + Σ ϕ ϵ ; θ ) ∣ ϵ ∼ N ( 0 , I ) ]
对抗生成网络GAN
https://en.wikipedia.org/wiki/Generative_adversarial_network Generative Adversarial Networks G ( z ; θ ) G(\bm{z};\bm{\theta}) G ( z ; θ ) D ( x ; ϕ ) D(\bm{x};\bm{\phi}) D ( x ; ϕ ) p g ( z ; θ ) p_\text{g}(\bm{z}; \bm{\theta}) p g ( z ; θ ) D ( x ; ϕ ) D(\bm{x};\bm{\phi}) D ( x ; ϕ ) D ( x ( G ) ; ϕ ) D\big( \bm{x}^{(G)}; \bm{\phi} \big) D ( x ( G ) ; ϕ )
J ( θ , ϕ ) = E x ∼ p data log D ( x ; ϕ ) + E x ( G ) ∼ p g ( x ∣ z ; θ ) log ( 1 − D ( x ( G ) ; ϕ ) ) = E x ∼ p data log D ( x ; ϕ ) + E z ∼ q ( z ) log ( 1 − D ( G ( z ; θ ) ; ϕ ) ) \begin{aligned}
\mathcal{J}(\bm{\theta}, \bm{\phi}) =& \mathbb{E}_{\bm{x}\sim p_\text{data}} \log D(\bm{x};\bm{\phi}) + \mathbb{E}_{\bm{x}^{(G)}\sim p_\text{g}(\bm{x} | \bm{z}; \bm{\theta})} \log \Big(1-D\big( \bm{x}^{(G)}; \bm{\phi} \big)\Big)\\
=& \mathbb{E}_{\bm{x}\sim p_\text{data}} \log D(\bm{x};\bm{\phi}) + \mathbb{E}_{\bm{z}\sim q(\bm{z})} \log \Big(1-D\big( G(\bm{z};\bm{\theta}); \bm{\phi} \big)\Big)
\end{aligned} J ( θ , ϕ ) = = E x ∼ p data log D ( x ; ϕ ) + E x ( G ) ∼ p g ( x ∣ z ; θ ) log ( 1 − D ( x ( G ) ; ϕ ) ) E x ∼ p data log D ( x ; ϕ ) + E z ∼ q ( z ) log ( 1 − D ( G ( z ; θ ) ; ϕ ) )
反向传播时,生成器与判别器分开优化,优化目标为:
arg min θ arg max ϕ J ( θ , ϕ ) \argmin_\bm{\theta} \argmax_\bm{\phi} \mathcal{J}(\bm{\theta}, \bm{\phi})
θ a r g m i n ϕ a r g m a x J ( θ , ϕ )
先固定生成器,调整判别器参数,最大化损失函数;之后,固定判别器,调整生成器参数,最小化损失,注意此时损失函数第一项不起作用。具体的:
更新判别器:
对数据和隐变量分别采样得到小批量样本{ x i , z i } \{\bm{x}^{i}, \bm{z}^{i}\} { x i , z i }
∇ ϕ 1 m ∑ i = 1 m [ log D ( x i ; ϕ ) + log ( 1 − D ( G ( z i ; θ ) ; ϕ ) ) ] \nabla_\bm{\phi}\frac{1}{m} \sum_{i=1}^{m} \left[ \log D(\bm{x}^{i};\bm{\phi}) + \log\Big(1-D\big( G(\bm{z}^{i};\bm{\theta}); \bm{\phi} \big)\Big)\right]
∇ ϕ m 1 i = 1 ∑ m [ log D ( x i ; ϕ ) + log ( 1 − D ( G ( z i ; θ ) ; ϕ ) ) ]
梯度上升 更新判别器的参数
重复采样和梯度上升k k k
更新生成器:
对隐变量分别采样得到小批量样本{ z j } \{\bm{z}^{j}\} { z j }
∇ θ 1 m ∑ j = 1 m log ( 1 − D ( G ( z j ; θ ) ; ϕ ) ) \nabla_\bm{\theta}\frac{1}{m} \sum_{j=1}^{m} \log\Big(1-D\big( G(\bm{z}^{j};\bm{\theta}); \bm{\phi} \big)\Big)
∇ θ m 1 j = 1 ∑ m log ( 1 − D ( G ( z j ; θ ) ; ϕ ) )
循环迭代,依次更新判别器和生成器
以上就是GAN的全部内容,其优化目标并不依赖通常的似然函数E x ∼ p ^ data log p g ( x ∣ z ; θ ) \mathbb{E}_{\bm{x}\sim \hat{p}_\text{data}} \log p_\text{g}(\bm{x} | \bm{z}; \bm{\theta}) E x ∼ p ^ data log p g ( x ∣ z ; θ ) p g ( x ∣ z ; θ ) → p data ( x ) p_\text{g}(\bm{x} | \bm{z}; \bm{\theta}) \rightarrow p_\text{data}(\bm{x}) p g ( x ∣ z ; θ ) → p data ( x )
数学理论基础
目标函数合理性 G ( x ) G(\bm{x}) G ( x ) p g ( x ∣ z ; θ ) p_\text{g}(\bm{x} | \bm{z}; \bm{\theta}) p g ( x ∣ z ; θ )
J ( θ , ϕ ) = E x ∼ p data log D ( x ; ϕ ) + E x ( G ) ∼ p g ( x ∣ z ; θ ) log ( 1 − D ( x ( G ) ; ϕ ) ) = ∫ p data ( x ) log D ( x ; ϕ ) + p g ( x ∣ z ; θ ) log ( 1 − D ( x ; ϕ ) ) d x \begin{aligned}
\mathcal{J}(\bm{\theta}, \bm{\phi}) =& \mathbb{E}_{\bm{x}\sim p_\text{data}} \log D(\bm{x};\bm{\phi}) + \mathbb{E}_{\bm{x}^{(G)}\sim p_\text{g}(\bm{x} | \bm{z}; \bm{\theta})} \log \Big(1-D\big( \bm{x}^{(G)}; \bm{\phi} \big)\Big)\\
=& \int p_\text{data}(\bm{x}) \log D(\bm{x};\bm{\phi}) + p_\text{g}(\bm{x} | \bm{z}; \bm{\theta}) \log \Big(1-D\big( \bm{x}; \bm{\phi} \big)\Big) d\bm{x}
\end{aligned} J ( θ , ϕ ) = = E x ∼ p data log D ( x ; ϕ ) + E x ( G ) ∼ p g ( x ∣ z ; θ ) log ( 1 − D ( x ( G ) ; ϕ ) ) ∫ p data ( x ) log D ( x ; ϕ ) + p g ( x ∣ z ; θ ) log ( 1 − D ( x ; ϕ ) ) d x
取任意x \bm{x} x p data ( x ) , p g ( x ∣ z ; θ ) p_\text{data}(\bm{x}), p_\text{g}(\bm{x} | \bm{z}; \bm{\theta}) p data ( x ) , p g ( x ∣ z ; θ ) D ( x ; ϕ ) D(\bm{x};\bm{\phi}) D ( x ; ϕ ) ∈ [ 0 , 1 ] {\small\in}[0,1] ∈ [ 0 , 1 ] y y y a log y + b log ( 1 − y ) a \log y + b\log(1-y) a log y + b log ( 1 − y ) [ 0 , 1 ] [0,1] [ 0 , 1 ] a a + b \frac{a}{a+b} a + b a G ( x ) G(\bm{x}) G ( x ) D ∗ ( x ) = p data ( x ) p data ( x ) + p g ( x ∣ z ; θ ) D^*(\bm{x}) = \frac{p_\text{data}(\bm{x})}{p_\text{data}(\bm{x})+p_\text{g}(\bm{x} | \bm{z}; \bm{\theta})} D ∗ ( x ) = p data ( x ) + p g ( x ∣ z ; θ ) p data ( x )
arg min θ arg max ϕ J ( θ , ϕ ) = arg min θ J ∗ ( θ ∣ D ( x ; ϕ ) = D ∗ ( x ) ) \argmin_\bm{\theta} \argmax_\bm{\phi} \mathcal{J}(\bm{\theta}, \bm{\phi}) = \argmin_\bm{\theta} \mathcal{J}^*\left(\bm{\theta}\Big|{\small D(\bm{x};\bm{\phi}) = D^*(\bm{x}) } \right)
θ a r g m i n ϕ a r g m a x J ( θ , ϕ ) = θ a r g m i n J ∗ ( θ ∣ ∣ ∣ ∣ D ( x ; ϕ ) = D ∗ ( x ) )
此时损失函数可表示为:
J ∗ ( θ ) = E x ∼ p data log p data ( x ) p data ( x ) + p g ( x ∣ z ; θ ) + E x ∼ p g ( x ∣ z ; θ ) log p g ( x ∣ z ; θ ) p data ( x ) + p g ( x ∣ z ; θ ) = D K L ( p data ∥ p data + p g 2 ) + D K L ( p g ∥ p data + p g 2 ) − 2 log 2 = 2 D J S ( p data ∥ p g ) − 2 log 2 \begin{aligned}
\mathcal{J}^*\left(\bm{\theta}\right) =& \mathbb{E}_{\bm{x}\sim p_\text{data}} \log \frac{p_\text{data}(\bm{x})}{p_\text{data}(\bm{x})+p_\text{g}(\bm{x} | \bm{z}; \bm{\theta})} + \mathbb{E}_{\bm{x}\sim p_\text{g}(\bm{x} | \bm{z}; \bm{\theta})} \log \frac{p_\text{g}(\bm{x} | \bm{z}; \bm{\theta})}{p_\text{data}(\bm{x})+p_\text{g}(\bm{x} | \bm{z}; \bm{\theta})}\\
=& D_{\rm KL}\left (p_\text{data} \Big\| \frac{p_\text{data}+p_\text{g}}{2} \right) +
D_{\rm KL}\left (p_\text{g} \Big\| \frac{p_\text{data}+p_\text{g}}{2} \right) -2\log 2\\
=& 2 D_{\rm JS}\big(p_\text{data} ~\|~ p_\text{g} \big) - 2\log 2
\end{aligned} J ∗ ( θ ) = = = E x ∼ p data log p data ( x ) + p g ( x ∣ z ; θ ) p data ( x ) + E x ∼ p g ( x ∣ z ; θ ) log p data ( x ) + p g ( x ∣ z ; θ ) p g ( x ∣ z ; θ ) D K L ( p data ∥ ∥ ∥ ∥ 2 p data + p g ) + D K L ( p g ∥ ∥ ∥ ∥ 2 p data + p g ) − 2 log 2 2 D J S ( p data ∥ p g ) − 2 log 2
其中D K L D_{\rm KL} D K L D J S D_{\rm JS} D J S 信息熵与统计距离 。为进行概率归一化,多了常数项− 2 log 2 -2\log2 − 2 log 2 p g = p data p_\text{g} = p_\text{data} p g = p data J m i n = − 2 log 2 {\small \mathcal{J}_{\rm min} = -2\log2} J m i n = − 2 log 2 p g ( x ∣ z ; θ ) = p data ( x ) p_\text{g}(\bm{x} | \bm{z}; \bm{\theta}) = p_\text{data}(\bm{x}) p g ( x ∣ z ; θ ) = p data ( x ) D ∗ ( x ) = p data ( x ) p data ( x ) + p g ( x ∣ z ; θ ) = 1 2 D^*(\bm{x}) = \frac{p_\text{data}(\bm{x})}{p_\text{data}(\bm{x})+p_\text{g}(\bm{x} | \bm{z}; \bm{\theta})} = \frac{1}{2} D ∗ ( x ) = p data ( x ) + p g ( x ∣ z ; θ ) p data ( x ) = 2 1 x \bm{x} x 1 2 \frac{1}{2} 2 1
算法收敛性 G G G D D D D D D G G G D ∗ D^* D ∗ D = D ∗ \small D=D^* D = D ∗ p g p_\text{g} p g
J ′ ( p g ) = sup D J ( G , D ) = E x ∼ p data log D ∗ ( x ) + E x ∼ p g log ( 1 − D ∗ ( x ) ) J'(p_g) = \sup_D J(G, D) =\mathbb{E}_{\bm{x}\sim p_\text{data}} \log D^*(\bm{x}) + \mathbb{E}_{\bm{x} \sim p_\text{g} } \log \big(1-D^*(\bm{x}) \big)
J ′ ( p g ) = D sup J ( G , D ) = E x ∼ p data log D ∗ ( x ) + E x ∼ p g log ( 1 − D ∗ ( x ) )
最小化损失等价于寻找p g p_\text{g} p g p g = p data p_\text{g} = p_\text{data} p g = p data p g p_\text{g} p g
每次迭代判别器都能达到最优解D ∗ D^* D ∗ k k k
生成器(及判别器)要有足够容量,从而可搜索整个函数空间,实际中网络参数有限,只能覆盖有限的函数空间,但最终实践的有效性侧面印证了算法的合理性。
最后,从博弈论角度理解,目标函数最优解对应于零和博弈下的纳什均衡状态,但纳什均衡要求判别器与生成器同时更新,而上面的算法则是判别器与生成器依次更新,两种情况下的最优解理论上并不一定相同。根据前面的讨论,在模型容量足够情况下,理论上依次更新是可以达到纳什均衡的。但GAN的很多后续很多改进都引入正则,限制了模型容量,此时无法保证p g = p data p_\text{g} = p_\text{data} p g = p data Do GANs always have Nash equilibria? 。
问题与改进
训练困难,损失不稳定
网络结构
目标函数D D D G G G p data p_\text{data} p data p g p_\text{g} p g
J ′ = sup D [ E x ∼ p data log D ( x ) + E x ∼ p g ( x ∣ z ; θ ) log ( 1 − D ( x ) ) ] = 2 D J S ( p data ∥ p g ) − 2 log 2 \begin{aligned}
J' &= \sup_D \Big[ \mathbb{E}_{\bm{x}\sim p_\text{data}} \log D(\bm{x}) + \mathbb{E}_{\bm{x}\sim p_\text{g}(\bm{x} | \bm{z}; \bm{\theta})} \log \big( 1-D(\bm{x}) \big) \Big]\\
&= 2 D_{\rm JS}\big(p_\text{data} ~\|~ p_\text{g} \big) - 2 \log 2
\end{aligned} J ′ = D sup [ E x ∼ p data log D ( x ) + E x ∼ p g ( x ∣ z ; θ ) log ( 1 − D ( x ) ) ] = 2 D J S ( p data ∥ p g ) − 2 log 2
理论上可在不影响全局最优前提下将JS散度扩展到其他统计距离,如f f f f f f 信息熵与统计距离 。对于f f f
D f ( p ∥ q ) = ∫ q ( x ) f ( p ( x ) q ( x ) ) d x = ∫ q ( x ) sup u ∈ dom f ∗ [ u p ( x ) q ( x ) − f ∗ ( u ) ] d x = u = D ( x ) sup D [ E x ∼ p data D ( x ) − E x ∼ p g f ∗ ( D ( x ) ) ] \begin{aligned}
D_f(p\|q) &= \int q(x)f\left(\frac{p(x)}{q(x)}\right)dx = \int q(x) \sup_{u\in \text{dom}_{f^*}} \left[u \frac{p(x)}{q(x)}-f^*(u)\right] dx\\
&\xlongequal{u=D(x)} \sup_D \Big[ \mathbb{E}_{\bm{x}\sim p_\text{data}} D(x) - \mathbb{E}_{\bm{x} \sim p_\text{g}} f^*\big(D(x)\big) \Big]
\end{aligned} D f ( p ∥ q ) = ∫ q ( x ) f ( q ( x ) p ( x ) ) d x = ∫ q ( x ) u ∈ dom f ∗ sup [ u q ( x ) p ( x ) − f ∗ ( u ) ] d x u = D ( x ) D sup [ E x ∼ p data D ( x ) − E x ∼ p g f ∗ ( D ( x ) ) ]
其中f ( t ) f(t) f ( t ) f ( 1 ) = 0 f(1)=0 f ( 1 ) = 0 f ( t ) f(t) f ( t ) f ( t ) = t log t f(t) = t\log t f ( t ) = t log t f ( t ) = sup u ∈ dom f ∗ [ u t − f ∗ ( u ) ] f(t) = \sup_{u\in \text{dom}_{f^*}} [u t - f^*(u)] f ( t ) = sup u ∈ dom f ∗ [ u t − f ∗ ( u ) ] f ∗ f^* f ∗ f f f f ∗ ( u ) = sup t ∈ dom f [ u t − f ( t ) ] f^*(u) = \sup_{t\in \text{dom}_{f}} [u t - f(t)] f ∗ ( u ) = sup t ∈ dom f [ u t − f ( t ) ] f f f f ∗ f^* f ∗ f f f f f f
WGAN-GP
不同分布间的Wasserstein距离为:
W ( p data , p g ) = inf γ ∼ Γ ( p data , p g ) E ( x , x ( G ) ) ∼ γ ∥ x − x ( G ) ∥ W(p_\text{data}, p_\text{g}) = \inf_{\gamma\sim\Gamma(p_\text{data}, p_\text{g})} \mathbb{E}_{(\bm{x}, \bm{x}^{(G)})\sim \gamma} \left\|\bm{x} -\bm{x}^{(G)}\right\|
W ( p data , p g ) = γ ∼ Γ ( p data , p g ) inf E ( x , x ( G ) ) ∼ γ ∥ ∥ ∥ ∥ x − x ( G ) ∥ ∥ ∥ ∥
其中γ \gamma γ p data , p g p_\text{data}, p_\text{g} p data , p g Γ \Gamma Γ d ( x , x ( G ) ) = ∥ x − x ( G ) ∥ d(\bm{x}, \bm{x}^{(G)}) = \left\|\bm{x} -\bm{x}^{(G)}\right\| d ( x , x ( G ) ) = ∥ ∥ ∥ x − x ( G ) ∥ ∥ ∥
W ( p data , p g ) = 1 K sup ∥ D ∥ L ≤ K [ E x ∼ p data D ( x ; ϕ ) − E x ∼ p g ( x ∣ z ; θ ) D ( x ; ϕ ) ] W(p_\text{data}, p_\text{g}) = \frac{1}{K}\sup_{\|D\|_L\le K} \Big[ \mathbb{E}_{\bm{x}\sim p_\text{data}} D(\bm{x};\bm{\phi}) - \mathbb{E}_{\bm{x} \sim p_\text{g}(\bm{x}|\bm{z};\bm{\theta})} D(\bm{x};\bm{\phi}) \Big]
W ( p data , p g ) = K 1 ∥ D ∥ L ≤ K sup [ E x ∼ p data D ( x ; ϕ ) − E x ∼ p g ( x ∣ z ; θ ) D ( x ; ϕ ) ]
其中D D D ∥ D ∥ L = ∣ D ( x 1 ) − D ( x 2 ) ∣ ∣ x 1 − x 2 ∣ \|D\|_L = \frac{|D(\bm{x}_1) -D(\bm{x}_2)|}{|\bm{x}_1-\bm{x}_2|} ∥ D ∥ L = ∣ x 1 − x 2 ∣ ∣ D ( x 1 ) − D ( x 2 ) ∣ x \bm{x} x D D D
更新判别器:
对数据和隐变量分别采样得到小批量样本{ x i , z i } \{\bm{x}^{i}, \bm{z}^{i}\} { x i , z i }
∇ ϕ 1 m ∑ i = 1 m [ D ( x i ; ϕ ) − D ( G ( z i ; θ ) ; ϕ ) ] \nabla_\bm{\phi}\frac{1}{m} \sum_{i=1}^{m} \left[D(\bm{x}^{i};\bm{\phi}) - D\Big( G(\bm{z}^{i};\bm{\theta}); \bm{\phi} \Big)\right]
∇ ϕ m 1 i = 1 ∑ m [ D ( x i ; ϕ ) − D ( G ( z i ; θ ) ; ϕ ) ]
梯度上升 更新判别器的参数
对参数做截断,限制任意判别器参数∣ ϕ ∣ < c |\phi| < c ∣ ϕ ∣ < c
重复采样和梯度上升k k k
更新生成器:
对隐变量分别采样得到小批量样本{ z j } \{\bm{z}^{j}\} { z j }
∇ θ 1 m ∑ j = 1 m D ( G ( z j ; θ ) ; ϕ ) \nabla_\bm{\theta}\frac{1}{m} \sum_{j=1}^{m} D\Big( G(\bm{z}^{j};\bm{\theta}); \bm{\phi} \Big)
∇ θ m 1 j = 1 ∑ m D ( G ( z j ; θ ) ; ϕ )
循环迭代,依次更新判别器和生成器
对比GAN,这其中核心的不同在于:
新的损失函数不再对判别器输出取对数
判别器参数始终被限制在指定范围
根据WGAN作者实验,随着生成器输出效果提升,JS散度不变甚至增加,而Wasserstein距离则稳步下降,进一步印证了后者的有效性。值得注意的,这里的“判别器”不具有判别数据属于真实数据的概率意义,不再输出(0, 1)的概率值,从而也不需要Sigmoid激活。这里的“判别器”只是构建Wasserstein距离的中间函数(拉格朗日乘子),原文中称之为critic(评价器)而非discriminator(判别器)。换句话说WGAN其实已经不遵从GAN中零和博弈的框架,这或许就是它训练相对稳定的原因。
WAGN相比GAN在训练稳定度上有了很大提升,但通过对判别器参数截断实现Lipschitz约束的操作,在实践中会出现梯度集中于边界值,网络结构相对简单,而在反向传递时又容易出现梯度发散或消失。对此,WGAN团队又提出可将Lipschitz约束作为损失函数的正则项,即引入梯度惩罚(Gradient Penalty)的WGAN-GP :
E x ∼ p data D ( x ; ϕ ) − E x ( G ) ∼ p g ( x ( G ) ∣ z ; θ ) D ( x ( G ) ; ϕ ) − λ E x ^ ∼ p x ^ ( ∥ ∇ x ^ D ( x ^ ; ϕ ) ∥ 2 − 1 ) 2 \mathbb{E}_{\bm{x}\sim p_\text{data}} D(\bm{x};\bm{\phi}) - \mathbb{E}_{\bm{x}^{(G)} \sim p_\text{g}(\bm{x}^{(G)}|\bm{z};\bm{\theta})} D(\bm{x}^{(G)};\bm{\phi}) - \lambda \mathbb{E}_{\bm{\hat{x}} \sim p_\bm{\hat{x}} } \big(\|\nabla_\bm{\hat{x}} D(\bm{\hat{x}};\bm{\phi})\|_2 -1\big)^2
E x ∼ p data D ( x ; ϕ ) − E x ( G ) ∼ p g ( x ( G ) ∣ z ; θ ) D ( x ( G ) ; ϕ ) − λ E x ^ ∼ p x ^ ( ∥ ∇ x ^ D ( x ^ ; ϕ ) ∥ 2 − 1 ) 2
显然这里梯度惩罚项不能对整个样本空间求期望,WGAN-GP中将x ^ \bm{\hat{x}} x ^ x \bm{x} x x ( G ) \bm{x}^{(G)} x ( G ) x ^ = ϵ x + ( 1 − ϵ ) x ( G ) = ϵ x + ( 1 − ϵ ) G ( z ; θ ) , ϵ ∈ U [ 0 , 1 ] \bm{\hat{x}} = \epsilon \bm{x} + (1-\epsilon)\bm{x}^{(G)} = \epsilon \bm{x} + (1-\epsilon)G(\bm{z}; \bm{\theta}), \epsilon\in U[0,1] x ^ = ϵ x + ( 1 − ϵ ) x ( G ) = ϵ x + ( 1 − ϵ ) G ( z ; θ ) , ϵ ∈ U [ 0 , 1 ] D ( x ) D(\bm{x}) D ( x ) x \bm{x} x x ( G ) \bm{x}^{(G)} x ( G ) x ( G ) = G ( z ; θ ) \bm{x}^{(G)}=G(\bm{z}; \bm{\theta}) x ( G ) = G ( z ; θ ) θ \bm{\theta} θ
E x ( G ) ∼ p g ( x ( G ) ∣ z ; θ ) D ( x ( G ) ; ϕ ) − E x ∼ p data D ( x ; ϕ ) + λ E x ^ ∼ p x ^ ( ∥ ∇ x ^ D ( x ^ ; ϕ ) ∥ 2 − 1 ) 2 \mathbb{E}_{\bm{x}^{(G)} \sim p_\text{g}(\bm{x}^{(G)}|\bm{z};\bm{\theta})} D(\bm{x}^{(G)};\bm{\phi}) - \mathbb{E}_{\bm{x}\sim p_\text{data}} D(\bm{x};\bm{\phi}) + \lambda \mathbb{E}_{\bm{\hat{x}} \sim p_\bm{\hat{x}} } \big(\|\nabla_\bm{\hat{x}} D(\bm{\hat{x}};\bm{\phi})\|_2 -1\big)^2
E x ( G ) ∼ p g ( x ( G ) ∣ z ; θ ) D ( x ( G ) ; ϕ ) − E x ∼ p data D ( x ; ϕ ) + λ E x ^ ∼ p x ^ ( ∥ ∇ x ^ D ( x ^ ; ϕ ) ∥ 2 − 1 ) 2
you can (and should) train the discriminator to convergence. If true, it would remove needing to balance generator updates with discriminator updates,
https://en.wikipedia.org/wiki/Generative_adversarial_network Wasserstein GAN From GAN to WGAN Read-through: Wasserstein GAN 令人拍案叫绝的Wasserstein GAN 互怼的艺术:从零直达 WGAN-GP
对偶 简单理解就是同一问题的不同视角,比如命题与逆反命题,集合的内部与外部,信号的时域与频域表示以及物质的波粒二象性等等。关于凸优化的拉格朗日对偶问题可参考深度学习入门 中关于凸优化的介绍。这里参照拉格朗日对偶对上面“莫名其妙”的变换做简单理解,不涉及证明。取W ( p , q ) = inf γ ∼ Γ ( p , q ) E ( x , y ) ∼ γ d ( x , y ) W(p, q) = \inf_{\gamma\sim\Gamma(p, q)} \mathbb{E}_{(x, y)\sim \gamma} d(x, y) W ( p , q ) = inf γ ∼ Γ ( p , q ) E ( x , y ) ∼ γ d ( x , y ) p ( x ) = ∫ γ ( x , y ) d y , q ( y ) = ∫ γ ( x , y ) d x p(x) = \int \gamma(x, y)dy, ~~ q(y) = \int \gamma(x, y) dx p ( x ) = ∫ γ ( x , y ) d y , q ( y ) = ∫ γ ( x , y ) d x
L ( p , q , f , g ) = ∫ d ( x , y ) d γ ( x , y ) + ∫ f ( x ) [ p ( x ) − ∫ γ ( x , y ) d y ] d x + ∫ g ( y ) [ q ( y ) − ∫ γ ( x , y ) d x ] d y = ∫ f ( x ) p ( x ) d x + ∫ g ( y ) q ( y ) d y + ∫ { d ( x , y ) − [ f ( x ) + g ( y ) ] } d γ ( x , y ) \begin{aligned}
L(p, q, f, g) =& \int d(x, y) d\gamma(x, y)\\
&+ \int f(x) \left[ p(x) - \int \gamma(x, y) dy \right] dx\\
&+ \int g(y) \left[q(y) - \int \gamma(x, y) dx \right] dy\\
=& \int f(x) p(x) dx + \int g(y) q(y) dy\\
& + \int \left\{d(x, y) - \left[f(x) + g(y) \right]\right\}d\gamma(x, y)
\end{aligned} L ( p , q , f , g ) = = ∫ d ( x , y ) d γ ( x , y ) + ∫ f ( x ) [ p ( x ) − ∫ γ ( x , y ) d y ] d x + ∫ g ( y ) [ q ( y ) − ∫ γ ( x , y ) d x ] d y ∫ f ( x ) p ( x ) d x + ∫ g ( y ) q ( y ) d y + ∫ { d ( x , y ) − [ f ( x ) + g ( y ) ] } d γ ( x , y )
这里f ( x ) , g ( y ) f(x),g(y) f ( x ) , g ( y ) W ( p , q ) \small W(p,q) W ( p , q )
W ( p , q ) = inf γ ∼ Γ ( p , q ) sup f , g L ( p , q , f , g ) = sup f , g inf γ ∼ Γ ( p , q ) L ( p , q , f , g ) = sup f , g [ ∫ f ( x ) p ( x ) d x + ∫ g ( y ) q ( y ) d y + inf γ ∼ Γ ( p , q ) ∫ { d ( x , y ) − [ f ( x ) + g ( y ) ] } d γ ( x , y ) ] \begin{aligned}
W(p,q) &= \inf_{\gamma\sim\Gamma(p, q)} \sup_{f, g} ~~ L(p, q, f, g) = \sup_{f, g} \inf_{\gamma\sim\Gamma(p, q)} L(p, q, f, g)\\
&= \sup_{f, g} \bigg[ \int f(x) p(x) dx + \int g(y) q(y) dy\\
& ~~~~~~~~~~~~ + \inf_{\gamma\sim\Gamma(p, q)} \int \left\{d(x, y) - \left[f(x) + g(y) \right]\right\}d\gamma(x, y) \bigg]
\end{aligned} W ( p , q ) = γ ∼ Γ ( p , q ) inf f , g sup L ( p , q , f , g ) = f , g sup γ ∼ Γ ( p , q ) inf L ( p , q , f , g ) = f , g sup [ ∫ f ( x ) p ( x ) d x + ∫ g ( y ) q ( y ) d y + γ ∼ Γ ( p , q ) inf ∫ { d ( x , y ) − [ f ( x ) + g ( y ) ] } d γ ( x , y ) ]
这里后一项求下限inf γ ∼ Γ ( p , q ) \inf_{\gamma\sim\Gamma(p, q)} inf γ ∼ Γ ( p , q ) f ( x ) + g ( y ) > d ( x , y ) f(x) + g(y) > d(x, y ) f ( x ) + g ( y ) > d ( x , y ) − ∞ -\infty − ∞ f ( x ) + g ( y ) ≤ d ( x , y ) f(x) + g(y) \le d(x, y ) f ( x ) + g ( y ) ≤ d ( x , y )
W ( p , q ) = sup f , g ∣ f ( x ) + g ( y ) ≤ d ( x , y ) [ ∫ f ( x ) p ( x ) d x + ∫ g ( y ) q ( y ) d y ] W(p,q) = \sup_{f, g ~|~ f(x) + g(y) \le d(x, y )} \bigg[ \int f(x) p(x) dx + \int g(y) q(y) dy\bigg]
W ( p , q ) = f , g ∣ f ( x ) + g ( y ) ≤ d ( x , y ) sup [ ∫ f ( x ) p ( x ) d x + ∫ g ( y ) q ( y ) d y ]
当概率空间为度量空间,对f , g f,g f , g g ( y ) = − f ( y ) g(y) = -f(y) g ( y ) = − f ( y )
sup f ( x ) − f ( y ) ≤ d ( x , y ) [ E x ∼ p f ( x ) − E y ∼ q f ( y ) ] = sup ∥ f ( x ) ∥ L ≤ 1 [ E x ∼ p f ( x ) − E y ∼ q f ( y ) ] \sup_{f(x) - f(y) \le d(x, y )} \Big[ \mathbb{E}_{x\sim p} f(x) - \mathbb{E}_{y\sim q} f(y) \Big] = \sup_{\|f(x)\|_L \le 1} \Big[ \mathbb{E}_{x\sim p} f(x) - \mathbb{E}_{y\sim q} f(y) \Big]
f ( x ) − f ( y ) ≤ d ( x , y ) sup [ E x ∼ p f ( x ) − E y ∼ q f ( y ) ] = ∥ f ( x ) ∥ L ≤ 1 sup [ E x ∼ p f ( x ) − E y ∼ q f ( y ) ]
基于流的生成模型NF
基于流的生成模型,或者说标准化流(Normalization flow)模型的思想可以说是各种生成模型中最直观的。其理论基础就是概率分布的变量代换。g g g
基于流的生成模型是最直观的,其理论基础就是概率分布的变量代换。其难点在于生成网络g g g x = g ( z ) \bm{x}=g(\bm{z}) x = g ( z ) ∣ det ( ∂ g ( z ) ∂ z ) ∣ \left|\det\left(\frac{\partial g(\bm{z})}{\partial\bm{z}}\right)\right| ∣ ∣ ∣ ∣ det ( ∂ z ∂ g ( z ) ) ∣ ∣ ∣ ∣ https://en.wikipedia.org/wiki/Flow-based_generative_model
q ( z ) = p ( g ( z ) ) ∣ det ( ∂ g ( z ) ∂ z ) ∣ ; p ( x ) = q ( g − 1 ( x ) ) ∣ det ( ∂ g ( z ) ∂ z ) ∣ − 1 q(\bm{z}) = p\left(g(\bm{z})\right) \left|\det\left(\frac{\partial g(\bm{z})}{\partial\bm{z}}\right)\right|; ~~~~~~ p(\bm{x}) = q\left(g^{-1}(\bm{x})\right) \left|\det\left(\frac{\partial g(\bm{z})}{\partial\bm{z}}\right)\right|^{-1}
q ( z ) = p ( g ( z ) ) ∣ ∣ ∣ ∣ ∣ det ( ∂ z ∂ g ( z ) ) ∣ ∣ ∣ ∣ ∣ ; p ( x ) = q ( g − 1 ( x ) ) ∣ ∣ ∣ ∣ ∣ det ( ∂ z ∂ g ( z ) ) ∣ ∣ ∣ ∣ ∣ − 1
arg max E x ∼ p data p ( x ) \argmax \mathbb{E}_{\bm{x}\sim p_\text{data}} p(\bm{x})
a r g m a x E x ∼ p data p ( x )
arg max E x ∼ p data [ log q ( g − 1 ( x ; θ ) ) − log ∣ det ( ∂ g ( z ; θ ) ∂ z ) ∣ ] \argmax \mathbb{E}_{\bm{x}\sim p_\text{data}} \left[ \log q\left(g^{-1}(\bm{x}; \bm{\theta})\right) - \log\left|\det\left(\frac{\partial g(\bm{z};\bm{\theta})}{\partial\bm{z}}\right)\right| \right]
a r g m a x E x ∼ p data [ log q ( g − 1 ( x ; θ ) ) − log ∣ ∣ ∣ ∣ ∣ det ( ∂ z ∂ g ( z ; θ ) ) ∣ ∣ ∣ ∣ ∣ ]
耦合流
一类较常见的可逆网络结构是“耦合层”(coupling layer):
输入数据被分为两部分[ z : m ; z m + 1 : ] [\bm{z}_{:m};\bm{z}_{m+1:}] [ z : m ; z m + 1 : ] f f f g g g g ( z m + 1 : ; θ ) = g ( z m + 1 : ; f ( z : m ) ) g(\bm{z}_{m+1:}; \bm{\theta}) = g\big(\bm{z}_{m+1:}; f(\bm{z}_{:m}) \big) g ( z m + 1 : ; θ ) = g ( z m + 1 : ; f ( z : m ) )
x = [ z : m ; g ( z m + 1 : ; f ( z : m ) ) ] ; z = [ x : m ; g − 1 ( x m + 1 : ; f ( x : m ) ) ] \bm{x} = [\bm{z}_{:m}; ~~ g\big(\bm{z}_{m+1:}; f(\bm{z}_{:m}) \big)]; ~~~~ \bm{z} = [\bm{x}_{:m}; ~~ g^{\tiny -1}\big(\bm{x}_{m+1:}; f(\bm{x}_{:m}) \big)]
x = [ z : m ; g ( z m + 1 : ; f ( z : m ) ) ] ; z = [ x : m ; g − 1 ( x m + 1 : ; f ( x : m ) ) ]
注意z : m = x : m , f ( z : m ) = f ( x : m ) \bm{z}_{:m} = \bm{x}_{:m}, f(\bm{z}_{:m}) = f(\bm{x}_{:m}) z : m = x : m , f ( z : m ) = f ( x : m ) g , g − 1 g, g^{\tiny -1} g , g − 1 f f f g g g f f f g g g g g g f f f g g g f f f g g g g g g 逐元素 (element-wise)操作时,右下角将成为对角阵,可极大减少行列式的计算量。最简单的情况下:
g ( z m + 1 : ; θ ) ) = z m + 1 : + θ g\big(\bm{z}_{m+1:}; \bm{\theta}) \big) = \bm{z}_{m+1:} + \bm{\theta}
g ( z m + 1 : ; θ ) ) = z m + 1 : + θ
右下角将是单位阵,行列式恒为1。这也是NICE中所提出的,
稍微复杂的是仿射耦合:
g ( z m + 1 : ; θ ) ) = θ 1 ⊙ z m + 1 : + θ 2 g\big(\bm{z}_{m+1:}; \bm{\theta}) \big) = \bm{\theta}_1 \odot \bm{z}_{m+1:} + \bm{\theta}_2
g ( z m + 1 : ; θ ) ) = θ 1 ⊙ z m + 1 : + θ 2
此时右下角是以 θ 1 \bm{\theta}_1 θ 1 θ 1 , θ 2 \bm{\theta}_1, \bm{\theta}_2 θ 1 , θ 2 f 1 ( z : m ) , f 2 ( z : m ) f_1(\bm{z}_{:m}), f_2(\bm{z}_{:m}) f 1 ( z : m ) , f 2 ( z : m ) 综述文章 。目前表达能力相对强的一类耦合函数是样条函数 ,如Neural Spline Flows 中提出的有理二次样条(Rational quadratic splines)。
自回归流
Autoregressive Flows https://mp.weixin.qq.com/s/XtlK3m-EHgFRKrtcwJHZCw https://mp.weixin.qq.com/s/oUQuHvy0lYco4HsocqvH3Q 正向KL散度 反向KL散度
正规化流A Family of Nonparametric Density Estimation Algorithms
基于正规化流的深度生成
问题
方法:
星系巡天观测盲源分离的技术:PCA, ICA, SMF
语音识别中声音分离的技术:这部分主要是神经网络
利用引力波特殊性质的技术:Chirp
反问题:站在更广的视角上,这个问题其实是典型的反问题。正向很简单,反向很困难,大部分的数据分析、参数推断都属于反问题,只是这个说法在天文领域不多见,在遥感和医学等领域更为常见。最近看到将深度网络与物理模型结合 来处理反问题的讨论,相关的技术能否借鉴,不过这部分还在调研,了解不多。
连续变换
扩散模型以及更一般的神经微分方程
泊松流
Poisson Flow Generative Models PFGM++: Unlocking the Potential of Physics-Inspired Generative Models
基于能量的生成模型
生成模型的核心目标是对数据的分布p ( x ) p(x) p ( x )
非负 p ( x ) ≥ 0 p(x) \ge 0 p ( x ) ≥ 0
归一 ∫ p ( x ) d x = 1 \int p(x) dx = 1 ∫ p ( x ) d x = 1
对任意函数f ( x ) f(x) f ( x ) ∣ f ∣ , f 2 , e f |f|, f^2, e^{f} ∣ f ∣ , f 2 , e f log ( 1 + e f ) \log(1 + e^{f}) log ( 1 + e f ) f ( x ; θ ) f(x;\theta) f ( x ; θ ) p ~ ( x ; θ ) \tilde{p}(x; \theta) p ~ ( x ; θ )
p ( x ; θ ) = p ~ ( x ; θ ) ∫ p ~ ( x ; θ ) d x = 1 Z ( θ ) p ~ ( x ; θ ) p(x; \theta) = \frac{\tilde{p}(x; \theta)}{\int \tilde{p}(x; \theta) dx} = \frac{1}{Z(\theta)}\tilde{p}(x; \theta)
p ( x ; θ ) = ∫ p ~ ( x ; θ ) d x p ~ ( x ; θ ) = Z ( θ ) 1 p ~ ( x ; θ )
Z ( θ ) = ∫ p ~ ( x ; θ ) d x Z(\theta) = \int \tilde{p}(x; \theta) dx Z ( θ ) = ∫ p ~ ( x ; θ ) d x p ~ ( x ; θ ) d x \tilde{p}(x; \theta) dx p ~ ( x ; θ ) d x f ( x ; θ ) f(x;\theta) f ( x ; θ ) f ( x ; θ ) f(x;\theta) f ( x ; θ ) p ~ ( x ; θ ) = e f ( x ; θ ) \tilde{p}(x; \theta) = e^{f(x; \theta)} p ~ ( x ; θ ) = e f ( x ; θ )
从直观上,可利用相对平滑的函数建模波动较大的分布
从数学上,指数族分布是概率论中很常见的一大类分布
从物理上,对应玻尔兹曼分布e − ε k T e^{-\frac{\varepsilon}{kT}} e − k T ε
对应于统计物理中的玻尔兹曼分布,通常称− f ( x ; θ ) -f(x; \theta) − f ( x ; θ ) 能量函数 ,而从这个视角出发的模型则被称为基于能量的生成模型,早期基于能量的无向图模型更是直接被称为玻尔兹曼机($16.2.4 of DL)。归一化因子Z ( θ ) Z(\theta) Z ( θ ) 配分函数 (partition function),同样来自统计物理。从统计物理视角,对应能量越低的状态x x x
考虑到要对整个样本空间积分,Z ( θ ) Z(\theta) Z ( θ )
E x ∼ p data ( x ) ∇ θ log p ( x ; θ ) = E x ∼ p data ( x ) ∇ θ log p ~ ( x ; θ ) − ∇ θ log Z ( θ ) \mathbb{E}_{x \sim p_\text{data}(x)} \nabla_{\theta} \log p(x; \theta) = \mathbb{E}_{x \sim p_\text{data}(x)} \nabla_{\theta} \log \tilde{p}(x; \theta) - \nabla_{\theta} \log Z(\theta)
E x ∼ p data ( x ) ∇ θ log p ( x ; θ ) = E x ∼ p data ( x ) ∇ θ log p ~ ( x ; θ ) − ∇ θ log Z ( θ )
注意,这里直接考虑(负)损失函数的梯度,而非损失函数本身。其中后一项:
∇ θ log Z ( θ ) = 1 Z ( θ ) ∇ θ Z ( θ ) = 1 Z ( θ ) ∇ θ ∫ p ~ ( x ; θ ) d x = 1 Z ( θ ) ∫ ∇ θ p ~ ( x ; θ ) d x \begin{aligned}
\nabla_{\theta} & \log Z(\theta) = \frac{1}{Z(\theta)}\nabla_{\theta} Z(\theta)\\
=& \frac{1}{Z(\theta)} \nabla_{\theta} \int \tilde{p}(x; \theta) dx = \frac{1}{Z(\theta)}\int \nabla_{\theta} \tilde{p}(x; \theta) dx\end{aligned} ∇ θ = log Z ( θ ) = Z ( θ ) 1 ∇ θ Z ( θ ) Z ( θ ) 1 ∇ θ ∫ p ~ ( x ; θ ) d x = Z ( θ ) 1 ∫ ∇ θ p ~ ( x ; θ ) d x
考虑到p ~ ( x ; θ ) > 0 \tilde{p}(x; \theta) > 0 p ~ ( x ; θ ) > 0 p ~ ( x ; θ ) = exp log p ~ ( x ; θ ) \tilde{p}(x; \theta) = \exp \log \tilde{p}(x; \theta) p ~ ( x ; θ ) = exp log p ~ ( x ; θ )
1 Z ( θ ) ∫ ∇ θ exp log p ~ ( x ; θ ) d x = 1 Z ( θ ) ∫ exp log p ~ ( x ; θ ) ∇ θ log p ~ ( x ; θ ) d x = 1 Z ( θ ) ∫ p ~ ( x ; θ ) ∇ θ log p ~ ( x ; θ ) d x = ∫ p ( x ; θ ) ∇ θ log p ~ ( x ; θ ) d x = E x ∼ p ( x ; θ ) ∇ θ log p ~ ( x ; θ ) \begin{aligned}
&\frac{1}{Z(\theta)}\int \nabla_{\theta} \exp \log \tilde{p}(x; \theta) dx\\
=& \frac{1}{Z(\theta)}\int \exp \log \tilde{p}(x; \theta) \nabla_{\theta} \log \tilde{p}(x; \theta) dx\\
=& \frac{1}{Z(\theta)}\int \tilde{p}(x; \theta) \nabla_{\theta} \log \tilde{p}(x; \theta) dx\\
=& \int p(x; \theta) \nabla_{\theta} \log \tilde{p}(x; \theta) dx
= \mathbb{E}_{x \sim p(x; \theta)} \nabla_{\theta} \log \tilde{p}(x; \theta)
\end{aligned} = = = Z ( θ ) 1 ∫ ∇ θ exp log p ~ ( x ; θ ) d x Z ( θ ) 1 ∫ exp log p ~ ( x ; θ ) ∇ θ log p ~ ( x ; θ ) d x Z ( θ ) 1 ∫ p ~ ( x ; θ ) ∇ θ log p ~ ( x ; θ ) d x ∫ p ( x ; θ ) ∇ θ log p ~ ( x ; θ ) d x = E x ∼ p ( x ; θ ) ∇ θ log p ~ ( x ; θ )
∇ θ J ( θ ) = − E x ∼ p data ( x ) ∇ θ log p ~ ( x ; θ ) + E x ∼ p ( x ; θ ) ∇ θ log p ~ ( x ; θ ) \nabla_{\theta} \mathcal{J}(\theta) = -\mathbb{E}_{x \sim p_\text{data}(x)} \nabla_{\theta} \log \tilde{p}(x; \theta) + \mathbb{E}_{x \sim p(x; \theta)} \nabla_{\theta} \log \tilde{p}(x; \theta)
∇ θ J ( θ ) = − E x ∼ p data ( x ) ∇ θ log p ~ ( x ; θ ) + E x ∼ p ( x ; θ ) ∇ θ log p ~ ( x ; θ )
对于基于能量的模型,p ~ ( x ; θ ) = e − E ( x ; θ ) \tilde{p}(x; \theta) = e^{-E(x; \theta)} p ~ ( x ; θ ) = e − E ( x ; θ )
∇ θ J ( θ ) = E x ∼ p data ( x ) ∇ θ E ( x ; θ ) − E x ∼ p ( x ; θ ) ∇ θ E ( x ; θ ) \nabla_{\theta} \mathcal{J}(\theta) = \mathbb{E}_{x \sim p_\text{data}(x)} \nabla_{\theta} E(x;\theta) - \mathbb{E}_{x \sim p(x; \theta)} \nabla_{\theta} E(x;\theta)
∇ θ J ( θ ) = E x ∼ p data ( x ) ∇ θ E ( x ; θ ) − E x ∼ p ( x ; θ ) ∇ θ E ( x ; θ )
注意不同于VAE、GAN或标准化流,基于能量的模型对“能量”建模,并未建立简单分布隐变量z z z z z z p ( x ; θ ) = 1 Z ( θ ) p ~ ( x ; θ ) p(x; \theta)=\frac{1}{Z(\theta)}\tilde{p}(x; \theta) p ( x ; θ ) = Z ( θ ) 1 p ~ ( x ; θ ) Z ( θ ) Z(\theta) Z ( θ ) p ~ ( x ; θ ) \tilde{p}(x; \theta) p ~ ( x ; θ ) p ~ ( x ; θ ) \tilde{p}(x; \theta) p ~ ( x ; θ )
在数据分布形式未知时,先利用神经网络学习目标分布的参数化形式,最后再对学习到的分布进行MCMC采样算法:从简单分布开始,经过马尔科夫迭代,逐渐收敛到目标分布。而在训练过程中
Thus to make maximum likelihood training feasible, likelihood-based models must either restrict their model architectures (e.g., causal convolutions in autoregressive models, invertible networks in normalizing flow models) to make
限制模型结构(causal convolutions in autoregressive models, invertible networks in normalizing flow models)来使得 Z θ = 1 Z_{\theta}=1 Zθ=1
近似规则化常数(variational inference in VAEs, or MCMC sampling used in contrastive divergence)
MCMC采样
f ( x ; θ ) f(x;\theta) f ( x ; θ ) Z ( θ ) Z(\theta) Z ( θ )
undirected graphical models cannot be normalized except in the Gaussian case.
基于得分的生成模型
需要使用MCMC采样避开配分函数,或借助变分推断近似估计配分函数
While the estimation of the gradient of log-density function is, in principle, a very difficult non-parametric problem.
minimizing the expected squared distance of the score function of x and the score function given by the model.
由于Z ( θ ) Z(\theta) Z ( θ ) E x ∼ p data ( x ) log p ( x ; θ ) \mathbb{E}_{x \sim p_\text{data}(x)} \log p(x; \theta) E x ∼ p data ( x ) log p ( x ; θ )
Hyvärinen 2005 提出得分匹配 ,以
此时优化时无需考虑配分函数,
J ( θ ) = 1 2 E x ∼ p data ( x ) ∥ ∇ x log p data ( x ) − ∇ x log p model ( x ) ∥ 2 \mathcal{J}(\theta) = \frac{1}{2}\mathbb{E}_{x \sim p_\text{data}(x)} \| \nabla_{x} \log p_\text{data}(x) - \nabla_{x} \log p_\text{model}(x)\|^2
J ( θ ) = 2 1 E x ∼ p data ( x ) ∥ ∇ x log p data ( x ) − ∇ x log p model ( x ) ∥ 2
只需要估计数据分布的梯度就可计算目标损失
其中对数似然(概率密度)关于随机变量的梯度 ∇ x log p ( x ) \nabla_{x} \log p(x) ∇ x log p ( x ) 得分函数 (score function),记:
s ( x ; θ ) = ∇ x log p ( x ; θ ) = ∇ x log p ~ ( x ; θ ) s ^ ( x ) = ∇ x log p data ( x ) = 1 p data ( x ) ∇ x p data ( x ) \begin{aligned}
\bm{s}(x;\theta) &= \nabla_{x} \log p(x; \theta) = \nabla_{x} \log \tilde{p}(x; \theta)\\
\hat{\bm{s}}(x) &= \nabla_{x} \log p_\text{data}(x) = \frac{1}{p_\text{data}(x)} \nabla_{x} p_\text{data}(x)
\end{aligned} s ( x ; θ ) s ^ ( x ) = ∇ x log p ( x ; θ ) = ∇ x log p ~ ( x ; θ ) = ∇ x log p data ( x ) = p data ( x ) 1 ∇ x p data ( x )
而对应的损失函数为:
J ( θ ) = 1 2 E x ∼ p data ( x ) ∥ s ^ ( x ) − s ( x ; θ ) ∥ 2 \mathcal{J}(\theta) = \frac{1}{2} \mathbb{E}_{x \sim p_\text{data}(x)} \| \hat{\bm{s}}(x) - \bm{s}(x;\theta) \|^2
J ( θ ) = 2 1 E x ∼ p data ( x ) ∥ s ^ ( x ) − s ( x ; θ ) ∥ 2
被称为得分匹配,即模型得分s ( x ; θ ) \bm{s}(x;\theta) s ( x ; θ ) s ^ ( x ) \hat{\bm{s}}(x) s ^ ( x )
得分函数的概念其实源自Fisher统计,通常将对数似然关于参数的梯度 称为Fisher得分函数(Fisher’s score function):
s ( x ∣ θ ) = ∇ θ log L ( x ∣ θ ) = ∑ i n ∇ θ log p ( x i ∣ θ ) \bm{s}(\mathbf{x}|\theta) = \nabla_\theta \log \mathcal{L}(\mathbf{x}|\theta) = \sum_i^n \nabla_\theta \log p(x_i|\theta)
s ( x ∣ θ ) = ∇ θ log L ( x ∣ θ ) = i ∑ n ∇ θ log p ( x i ∣ θ )
进一步的,可以定义得分函数的期望和方差。
E { s ( x ∣ θ ) } = ∫ ∇ θ log L ( x ∣ θ ) p ( x ; θ ^ ) d x \mathbb{E} \{\bm{s}(\mathbf{x}|\theta)\} = \int \nabla_\theta \log \mathcal{L}(\mathbf{x}|\theta) ~~ p(\mathbf{x};\hat{\theta}) d\mathbf{x}
E { s ( x ∣ θ ) } = ∫ ∇ θ log L ( x ∣ θ ) p ( x ; θ ^ ) d x
这里期望是将整个观测数据集x \mathbf{x} x p ( x ; θ ^ ) p(\mathbf{x};\hat{\theta}) p ( x ; θ ^ ) p ( x ; θ ) = L ( x ∣ θ ) p(\mathbf{x};\theta)=\mathcal{L}(\mathbf{x}|\theta) p ( x ; θ ) = L ( x ∣ θ ) θ ^ \hat{\theta} θ ^
E { s ( x ∣ θ ^ ) } = ∫ ∇ θ log L ( x ∣ θ ) ∣ θ ^ p ( x ; θ ^ ) d x = ∫ ∇ θ L ( x ∣ θ ) L ( x ∣ θ ) p ( x ; θ ) ∣ θ ^ d x = ∫ ∇ θ L ( x ∣ θ ) d x ∣ θ ^ = [ ∇ θ ∫ p ( x ; θ ) d x ] ∣ θ ^ = ∇ θ 1 = 0 \begin{aligned}
\mathbb{E} \{\bm{s}(\mathbf{x}|\hat{\theta})\} &= \int \nabla_\theta \log \mathcal{L}(\mathbf{x}|\theta)\big|_{\hat{\theta}} ~~ p(\mathbf{x};\hat{\theta}) d\mathbf{x}
= \int \frac{\nabla_\theta \mathcal{L}(\mathbf{x}|\theta)}{\mathcal{L}(\mathbf{x}|\theta)} ~ p(\mathbf{x};\theta)\Big|_{\hat{\theta}} ~ d\mathbf{x}\\
& = \int\nabla_\theta \mathcal{L}(\mathbf{x}|\theta) ~ d\mathbf{x} ~~\bigg|_{\hat{\theta}}
= \left[\nabla_\theta \int p(\mathbf{x}; \theta) d\mathbf{x}\right]\bigg|_{\hat{\theta}} = \nabla_\theta ~ 1 = 0
\end{aligned} E { s ( x ∣ θ ^ ) } = ∫ ∇ θ log L ( x ∣ θ ) ∣ ∣ ∣ θ ^ p ( x ; θ ^ ) d x = ∫ L ( x ∣ θ ) ∇ θ L ( x ∣ θ ) p ( x ; θ ) ∣ ∣ ∣ ∣ θ ^ d x = ∫ ∇ θ L ( x ∣ θ ) d x ∣ ∣ ∣ ∣ ∣ θ ^ = [ ∇ θ ∫ p ( x ; θ ) d x ] ∣ ∣ ∣ ∣ ∣ θ ^ = ∇ θ 1 = 0
即得分函数在参数真值处期望为0,此时得分函数方差可简化为(仅在参数真值成立):
I ( θ ) = V a r { s ( x ∣ θ ) } = E { s ( x ∣ θ ) s T ( x ∣ θ ) } \mathcal{I}(\theta) = {\rm Var} \{\bm{s}(\mathbf{x}| \theta)\} = \mathbb{E} \{ \bm{s}(\mathbf{x}| \theta)\bm{s}^T(x| \theta)\}
I ( θ ) = V a r { s ( x ∣ θ ) } = E { s ( x ∣ θ ) s T ( x ∣ θ ) }
可以证明,参数真值处得分函数方差等于负的黑塞矩阵的期望。
E { ∇ θ ∇ θ T log L ( x ∣ θ ) ∣ θ ^ } + E { s ( x ∣ θ ^ ) s T ( x ∣ θ ^ ) } = ∫ [ ∇ θ ∇ θ T log L ( x ∣ θ ) + ∇ θ log L ( x ∣ θ ) ∇ θ T log L ( x ∣ θ ) ] ∣ θ ^ p ( x ; θ ^ ) d x = ∫ [ ∇ θ ∇ θ T log L ( x ∣ θ ) p ( x ; θ ) + ∇ θ log L ( x ∣ θ ) ∇ θ T L ( x ∣ θ ) ] d x ∣ θ ^ = ∫ ∇ θ [ ∇ θ log L ( x ∣ θ ) p ( x ; θ ) ] d x ∣ θ ^ = ∫ ∇ θ [ ∇ θ L ( x ∣ θ ) ] d x ∣ θ ^ = [ ∇ θ ∇ θ T ∫ L ( x ∣ θ ) d x ] ∣ θ ^ = ∇ θ ∇ θ T 1 = 0 \begin{aligned}
& \mathbb{E} \{ \nabla_\theta \nabla^T_\theta \log \mathcal{L}(\mathbf{x}|\theta)\big|_{\hat{\theta}} \} + \mathbb{E} \{ \bm{s}(\mathbf{x}| \hat{\theta})\bm{s}^T(x| \hat{\theta})\} \\
=& \int \left[\nabla_\theta \nabla^T_\theta\log \mathcal{L}(\mathbf{x}|\theta) + \nabla_\theta \log \mathcal{L}(\mathbf{x}|\theta) \nabla^T_\theta \log \mathcal{L}(\mathbf{x}|\theta)\right]\big|_{\hat{\theta}} ~~ p(\mathbf{x};\hat{\theta})~ d\mathbf{x}\\
=& \int \left[\nabla_\theta \nabla^T_\theta\log \mathcal{L}(\mathbf{x}|\theta) ~~ p(\mathbf{x};\theta) + \nabla_\theta \log \mathcal{L}(\mathbf{x}|\theta) \nabla^T_\theta \mathcal{L}(\mathbf{x}|\theta)\right]~ d\mathbf{x} ~~ \bigg|_{\hat{\theta}}\\
=& \int \nabla_\theta \big[\nabla_\theta \log \mathcal{L}(\mathbf{x}|\theta) ~~ p(\mathbf{x};\theta) \big]~ d\mathbf{x} ~~\bigg|_{\hat{\theta}} = \int \nabla_\theta \big[\nabla_\theta \mathcal{L}(\mathbf{x}|\theta) \big]~ d\mathbf{x}~~\bigg|_{\hat{\theta}}\\
=& \left[\nabla_\theta \nabla^T_\theta \int \mathcal{L}(\mathbf{x}|\theta)~ d\mathbf{x} \right] \bigg|_{\hat{\theta}} = \nabla_\theta \nabla^T_\theta ~ 1 = 0
\end{aligned} = = = = E { ∇ θ ∇ θ T log L ( x ∣ θ ) ∣ ∣ ∣ θ ^ } + E { s ( x ∣ θ ^ ) s T ( x ∣ θ ^ ) } ∫ [ ∇ θ ∇ θ T log L ( x ∣ θ ) + ∇ θ log L ( x ∣ θ ) ∇ θ T log L ( x ∣ θ ) ] ∣ ∣ ∣ θ ^ p ( x ; θ ^ ) d x ∫ [ ∇ θ ∇ θ T log L ( x ∣ θ ) p ( x ; θ ) + ∇ θ log L ( x ∣ θ ) ∇ θ T L ( x ∣ θ ) ] d x ∣ ∣ ∣ ∣ ∣ θ ^ ∫ ∇ θ [ ∇ θ log L ( x ∣ θ ) p ( x ; θ ) ] d x ∣ ∣ ∣ ∣ ∣ θ ^ = ∫ ∇ θ [ ∇ θ L ( x ∣ θ ) ] d x ∣ ∣ ∣ ∣ ∣ θ ^ [ ∇ θ ∇ θ T ∫ L ( x ∣ θ ) d x ] ∣ ∣ ∣ ∣ ∣ θ ^ = ∇ θ ∇ θ T 1 = 0
由此:
I ( θ ^ ) = E { s ( x ∣ θ ^ ) s T ( x ∣ θ ^ ) } = − E { ∇ θ ∇ θ T log L ( x ∣ θ ) ∣ θ ^ } \mathcal{I}(\hat{\theta}) = \mathbb{E} \{ \bm{s}(\mathbf{x}| \hat{\theta})\bm{s}^T(x| \hat{\theta})\} = - \mathbb{E} \{ \nabla_\theta \nabla^T_\theta \log \mathcal{L}(\mathbf{x}|\theta)\big|_{\hat{\theta}} \}
I ( θ ^ ) = E { s ( x ∣ θ ^ ) s T ( x ∣ θ ^ ) } = − E { ∇ θ ∇ θ T log L ( x ∣ θ ) ∣ ∣ ∣ θ ^ }
根据概率乘法公式,独立事件的Fisher信息(矩阵)具有可加性,此外费雪信息矩阵为正定,
θ ˉ ∼ N ( θ ^ , I − 1 ( θ ^ ) ) ; I ( θ ^ ) ( θ ˉ − θ ^ ) → N ( 0 , 1 ) \bar{\theta} \sim \mathcal{N}(\hat{\theta}, I^{-1}(\hat{\theta}) ); ~~~ \sqrt{I(\hat{\theta})}(\bar{\theta}-\hat{\theta}) \rightarrow \mathcal{N}(0, 1)
θ ˉ ∼ N ( θ ^ , I − 1 ( θ ^ ) ) ; I ( θ ^ ) ( θ ˉ − θ ^ ) → N ( 0 , 1 )
即费雪信息矩阵的逆对应MLE估计的协方差矩阵。考虑到Fisher信息的可加性,对于独立观测,随着样本数n n n I ( θ ^ ) ∝ n I(\hat{\theta})\propto n I ( θ ^ ) ∝ n ∝ 1 n \propto \frac{1}{\sqrt{n}} ∝ n 1
费雪信息是对观测数据x x x θ \theta θ
Thus, the information contained in x about the true value of some parameter θ of the presumed distribution of x, has an inverse relation with the variance of the partial derivative w.r.t. θ of the log-likelihood function.
V a r ( θ ^ ) ≥ I − 1 ( θ ) {\rm Var}(\hat{\theta}) \ge \mathcal{I}^{-1}(\theta)
V a r ( θ ^ ) ≥ I − 1 ( θ )
The Fisher information is a way of measuring the amount of information that an observable random variable X X carries about an unknown parameter θ \theta upon which the probability of X X depends.
Fisher信息定义为得分函数的方差(协方差矩阵)
E { ∥ s ( x ; θ ) ∥ 2 } \mathbb{E} \left\{ \| \bm{s}(x; \theta) \|^2 \right\}
E { ∥ s ( x ; θ ) ∥ 2 }
Fisher
KL散度源自Shannon信息熵,而Fisher散度源自Fisher信息。费雪散度 (Fisher Divergence):
D F ( p ∣ q ) = 1 2 E x ∼ p ( x ) ∥ ∇ x log p ( x ) − ∇ x log p ( x ) ∥ 2 = 1 2 E x ∼ p ( x ) ∥ ∇ x log p ( x ) q ( x ) ∥ 2 D_{\rm F}(p|q) = \frac{1}{2}\mathbb{E}_{x\sim p(x)} \left\|\nabla_x \log p(x) - \nabla_x \log p(x)\right\|^2 = \frac{1}{2}\mathbb{E}_{x\sim p(x)} \left\|\nabla_x \log\frac{p(x)}{q(x)}\right\|^2
D F ( p ∣ q ) = 2 1 E x ∼ p ( x ) ∥ ∇ x log p ( x ) − ∇ x log p ( x ) ∥ 2 = 2 1 E x ∼ p ( x ) ∥ ∥ ∥ ∥ ∥ ∇ x log q ( x ) p ( x ) ∥ ∥ ∥ ∥ ∥ 2
可以证明:
D F ( p ~ ∣ q ~ ) = − d d t D K L ( p ~ ∣ q ~ ) D_{\rm F}(\tilde{p}|\tilde{q}) = -\frac{d}{dt} D_{\rm KL}(\tilde{p}|\tilde{q})
D F ( p ~ ∣ q ~ ) = − d t d D K L ( p ~ ∣ q ~ )
特别地,当t t t
D F ( p ∣ q ) = − d d t D K L ( p ~ ∣ q ~ ) ∣ t = 0 D_{\rm F}(p|q) = -\frac{d}{dt} D_{\rm KL}(\tilde{p}|\tilde{q})|_{t=0}
D F ( p ∣ q ) = − d t d D K L ( p ~ ∣ q ~ ) ∣ t = 0
不过数据的梯度,即s ^ ( x ) \hat{\bm{s}}(x) s ^ ( x ) Hyvärinen 2005 发现,通过简单变换就可绕开s ^ ( x ) \hat{\bm{s}}(x) s ^ ( x )
E x ∼ p data ( x ) [ ∥ s ^ ( x ) ∥ 2 + ∥ s ( x ; θ ) ∥ 2 − 2 s ^ T ( x ) s ( x ; θ ) ] \mathbb{E}_{x \sim p_\text{data}(x)} \left[ \| \hat{\bm{s}}(x)\|^2 + \|\bm{s}(x;\theta) \|^2 - 2 \hat{\bm{s}}^T(x)\bm{s}(x;\theta) \right]
E x ∼ p data ( x ) [ ∥ s ^ ( x ) ∥ 2 + ∥ s ( x ; θ ) ∥ 2 − 2 s ^ T ( x ) s ( x ; θ ) ]
其中第一项只与x x x
E x [ s ^ T ( x ) s ( x ; θ ) ] = ∫ p data ( x ) s ^ T ( x ) s ( x ; θ ) d x = ∫ p data ( x ) ∇ x T p data ( x ) p data ( x ) s ( x ; θ ) d x = ∫ ∇ x T p data ( x ) s ( x ; θ ) d x = p data ( x ) s ( x ; θ ) ∣ − ∞ + ∞ − ∫ p data ( x ) ∇ x T s ( x ; θ ) d x = − E x t r ( ∇ x s ( x ; θ ) ) \begin{aligned}
&\mathbb{E}_{x} [\hat{\bm{s}}^T(x)\bm{s}(x;\theta)] = \int p_\text{data}(x) \hat{\bm{s}}^T(x) \bm{s}(x;\theta) dx\\
& = \int p_\text{data}(x) \frac{\nabla_{x}^T p_\text{data}(x)}{p_\text{data}(x)} \bm{s}(x;\theta) dx = \int \nabla_{x}^T p_\text{data}(x) \bm{s}(x;\theta) dx\\
& = p_\text{data}(x) \bm{s}(x;\theta)|_{-\infty}^{+\infty} - \int p_\text{data}(x) \nabla_{x}^T \bm{s}(x;\theta) dx = - \mathbb{E}_{x} ~ {\rm tr}\big(\nabla_{x} \bm{s}(x;\theta)\big)
\end{aligned} E x [ s ^ T ( x ) s ( x ; θ ) ] = ∫ p data ( x ) s ^ T ( x ) s ( x ; θ ) d x = ∫ p data ( x ) p data ( x ) ∇ x T p data ( x ) s ( x ; θ ) d x = ∫ ∇ x T p data ( x ) s ( x ; θ ) d x = p data ( x ) s ( x ; θ ) ∣ − ∞ + ∞ − ∫ p data ( x ) ∇ x T s ( x ; θ ) d x = − E x t r ( ∇ x s ( x ; θ ) )
这里假设p data ( x ) → 0 , ∣ x ∣ → ∞ p_\text{data}(x) \rightarrow 0, |x| \rightarrow \infty p data ( x ) → 0 , ∣ x ∣ → ∞ s ( x ; θ ) \bm{s}(x;\theta) s ( x ; θ )
J ( θ ) = 1 2 E x ∼ p data ( x ) ∥ s ^ ( x ) − s ( x ; θ ) ∥ 2 = E x ∼ p data ( x ) [ 1 2 ∥ s ( x ; θ ) ∥ 2 + t r ( ∇ x s ( x ; θ ) ) ] + const. = E x ∼ p data ( x ) [ 1 2 ∥ ∇ x log p ~ ( x ; θ ) ∥ 2 + ∇ x 2 log p ~ ( x ; θ ) ] + const. \begin{aligned}
\mathcal{J}(\theta) &= \frac{1}{2} \mathbb{E}_{x \sim p_\text{data}(x)} \| \hat{\bm{s}}(x) - \bm{s}(x;\theta) \|^2\\
& = \mathbb{E}_{x \sim p_\text{data}(x)} \left[ \frac{1}{2}\| \bm{s}(x; \theta) \|^2 + {\rm tr}\big(\nabla_{x} \bm{s}(x;\theta)\big) \right] + \text{const.}\\
& = \mathbb{E}_{x \sim p_\text{data}(x)} \left[ \frac{1}{2}\| \nabla_{x} \log \tilde{p}(x; \theta) \|^2 + \nabla^2_{x} \log \tilde{p}(x; \theta)\right] + \text{const.}
\end{aligned} J ( θ ) = 2 1 E x ∼ p data ( x ) ∥ s ^ ( x ) − s ( x ; θ ) ∥ 2 = E x ∼ p data ( x ) [ 2 1 ∥ s ( x ; θ ) ∥ 2 + t r ( ∇ x s ( x ; θ ) ) ] + const. = E x ∼ p data ( x ) [ 2 1 ∥ ∇ x log p ~ ( x ; θ ) ∥ 2 + ∇ x 2 log p ~ ( x ; θ ) ] + const.
其中∇ 2 \nabla^2 ∇ 2 ∇ x 2 log p ~ ( x ; θ ) = ∑ i ∂ 2 log p ~ ( x ; θ ) ∂ x i \nabla^2_x\log \tilde{p}(\bm{x}; \theta) = \sum_i \frac{\partial^2 \log \tilde{p}(\bm{x}; \theta)}{\partial x_i} ∇ x 2 log p ~ ( x ; θ ) = ∑ i ∂ x i ∂ 2 l o g p ~ ( x ; θ ) O ( D ) O(D) O ( D ) Sliced Score Matching :
J ′ ( θ ) = 1 2 E v ∼ p v E x ∼ p data ( x ) ∥ v T [ s ^ ( x ) − s ( x ; θ ) ] ∥ 2 = E v ∼ p v E x ∼ p data ( x ) [ 1 2 ( v T s ( x ; θ ) ) 2 + v T ∇ x s ( x ; θ ) v ] + const. \begin{aligned}
\mathcal{J}'(\theta) &= \frac{1}{2} \mathbb{E}_{\mathbf{v} \sim p_\mathbf{v}} \mathbb{E}_{x \sim p_\text{data}(x)} \left\| \mathbf{v}^T\big[\hat{\bm{s}}(x) - \bm{s}(x;\theta)\big] \right\|^2\\
& = \mathbb{E}_{\mathbf{v} \sim p_\mathbf{v}} \mathbb{E}_{x \sim p_\text{data}(x)} \left[ \frac{1}{2}\big(\mathbf{v}^T\bm{s}(x; \theta) \big)^2 + \mathbf{v}^T ~ \nabla_{x} \bm{s}(x;\theta) ~ \mathbf{v} \right] + \text{const.}\end{aligned} J ′ ( θ ) = 2 1 E v ∼ p v E x ∼ p data ( x ) ∥ ∥ ∥ v T [ s ^ ( x ) − s ( x ; θ ) ] ∥ ∥ ∥ 2 = E v ∼ p v E x ∼ p data ( x ) [ 2 1 ( v T s ( x ; θ ) ) 2 + v T ∇ x s ( x ; θ ) v ] + const.
其中v \mathbf{v} v p v p_\mathbf{v} p v
ResNetscore matching -> flow matching(Lipman et al. 2022)
使用神经网络参数化隐藏状态的导数,而不是如往常那样直接参数化隐藏状态。这里参数化隐藏状态的导数就类似构建了连续性的层级与参数,而不再是离散的层级。因此参数也是一个连续的空间,我们不需要再分层传播梯度与更新参数。理论上,使用 ODE 求解器能够根据给定的误差容忍度选择适当的步长逼近真实解。ODE 求解器并不总是有效。
前向过程:ODE Solver torchdiffeq
Neural ODE,这个世界终究是连续的 神经网络常微分方程 (Neural ODEs) 解析 https://jiangsiyuan.com/2019/03/20/Neural ODE/
https://julialang.org/blog/2019/01/fluxdiffeq/#what_is_the_neural_ordinary_differential_equation_ode
基于ODENet的标准化流
扩散概率模型DPM
概率扩散模型由Sohl-Dickstein等人于2015年提出,之后DDPM借助重参数化技巧有效简化了模型的训练,实现了真正的突破。如上图所示扩散模型包含由数据到隐变量的前向扩散和由隐变量到数据的反向扩散。其中前向扩散过程为马尔科夫过程,q ( x t ∣ x t − 1 ) q(x_t|x_{t-1}) q ( x t ∣ x t − 1 ) β t ∈ [ 0 , 1 ] \beta_t\in[0,1] β t ∈ [ 0 , 1 ]
q ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t x t − 1 , β t I ) q(x_t|x_{t-1}) = \mathcal{N}(x_t; \sqrt{1-\beta_t}x_{t-1}, \beta_t I)
q ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t x t − 1 , β t I )
即给定x t − 1 x_{t-1} x t − 1 x t x_t x t q ( x t ∣ x t − 1 ) q(x_t|x_{t-1}) q ( x t ∣ x t − 1 ) β t \beta_t β t x t x_t x t x t = 1 − β t x t − 1 + β t ϵ t − 1 x_t = \sqrt{1-\beta_t}x_{t-1} + \sqrt{\beta_t}\epsilon_{t-1} x t = 1 − β t x t − 1 + β t ϵ t − 1 ϵ t − 1 \epsilon_{t-1} ϵ t − 1 x 0 x_0 x 0
x t = α t x 0 + 1 − α t ϵ , ϵ ∼ N ( 0 , I ) x_t = \sqrt{\alpha_t}x_0 + \sqrt{1- \alpha_t}\epsilon, \epsilon \sim \mathcal{N}(0, I)
x t = α t x 0 + 1 − α t ϵ , ϵ ∼ N ( 0 , I )
其中α t = ∏ s = 1 t ( 1 − β s ) \alpha_t = \prod_{s=1}^t (1-\beta_s) α t = ∏ s = 1 t ( 1 − β s ) x 0 x_0 x 0 x t x_t x t q ( x t ∣ x 0 ) = N ( x t ; α t x 0 , ( 1 − α t ) I ) q(x_t|x_0) = \mathcal{N}\big(x_t; \sqrt{\alpha_t}x_0, (1-\alpha_t)I\big) q ( x t ∣ x 0 ) = N ( x t ; α t x 0 , ( 1 − α t ) I ) β t ∈ [ 0 , 1 ] \beta_t\in[0,1] β t ∈ [ 0 , 1 ] x t x_t x t β t \beta_t β t β t \beta_t β t β 1 < β 2 < . . . < β T \beta_1 < \beta_2 < ... < \beta_T β 1 < β 2 < . . . < β T U-Net ,且参数在所有扩散步间共享 ,通过额外的时间向量(time embedding)指示当前扩散步数。此外在训练时,对于各扩散步DDPM并未按顺序逐个计算,而是直接随机采样,训练完成后的生成过程才依次反向扩散。
DPM
关于目标函数(似然函数)的具体推导可参考Sohl-Dickstein et al. (2015) :
L = E x ∼ p data log p model ( x ) = E x 0 ∼ q ( x 0 ) log p model ( x 0 ) = E x 0 ∼ q ( x 0 ) log ∫ p ( x 0 , . . . , x T ) d x 1 . . . d x T = E x 0 ∼ q ( x 0 ) log ∫ q ( x 1 , . . . , x T ∣ x 0 ) p ( x 0 , . . . , x T ) q ( x 1 , . . . , x T ∣ x 0 ) d x 1 . . . d x T = E x 0 ∼ q ( x 0 ) log E ( x 1 , . . . x T ) ∼ q ( x 1 , . . . , x T ∣ x 0 ) p ( x 0 , . . . , x T ) q ( x 1 , . . . , x T ∣ x 0 ) ≥ E x 0 ∼ q ( x 0 ) E ( x 1 , . . . x T ) ∼ q ( x 1 , . . . , x T ∣ x 0 ) log p ( x 0 , . . . , x T ) q ( x 1 , . . . , x T ∣ x 0 ) = E ( x 0 , x 1 , . . . x T ) ∼ q ( x 0 , x 1 , . . . , x T ) log p ( x 0 , . . . , x T ) q ( x 1 , . . . , x T ∣ x 0 ) = E ( x 0 , x 1 , . . . x T ) ∼ q ( x 0 , x 1 , . . . , x T ) [ log p ( x T ) + ∑ t = 1 T log p ( x t − 1 ∣ x t ) q ( x t ∣ x t − 1 ) ] \begin{aligned}
\mathcal{L} &= \mathbb{E}_{\bm{x}\sim p_\text{data}} ~ \log p_\text{model}(\bm{x}) =\mathbb{E}_{x_0\sim q(x_0)} ~ \log p_\text{model}(x_0)\\
&= \mathbb{E}_{x_0\sim q(x_0)} \log \int p(x_0, ..., x_T) d x_1 ... d x_T\\
&= \mathbb{E}_{x_0\sim q(x_0)} \log \int q(x_1, ..., x_T|x_0) \frac{p(x_0, ..., x_T)}{q(x_1, ..., x_T|x_0)} d x_1 ... d x_T\\
&= \mathbb{E}_{x_0\sim q(x_0)} \log \mathbb{E}_{(x_1, ... x_T)\sim q(x_1, ..., x_T|x_0)} \frac{p(x_0, ..., x_T)}{q(x_1, ..., x_T|x_0)} \\
&\ge \mathbb{E}_{x_0\sim q(x_0)} \mathbb{E}_{(x_1, ... x_T)\sim q(x_1, ..., x_T|x_0)} \log \frac{p(x_0, ..., x_T)}{q(x_1, ..., x_T|x_0)} \\
&= \mathbb{E}_{(x_0, x_1, ... x_T)\sim q(x_0, x_1, ..., x_T)} \log \frac{p(x_0, ..., x_T)}{q(x_1, ..., x_T|x_0)} \\
&= \mathbb{E}_{(x_0, x_1, ... x_T)\sim q(x_0, x_1, ..., x_T)} \left[ \log p(x_T) + \sum_{t=1}^T \log \frac{p(x_{t-1}|x_t)}{q(x_t|x_{t-1})}\right]
\end{aligned} L = E x ∼ p data log p model ( x ) = E x 0 ∼ q ( x 0 ) log p model ( x 0 ) = E x 0 ∼ q ( x 0 ) log ∫ p ( x 0 , . . . , x T ) d x 1 . . . d x T = E x 0 ∼ q ( x 0 ) log ∫ q ( x 1 , . . . , x T ∣ x 0 ) q ( x 1 , . . . , x T ∣ x 0 ) p ( x 0 , . . . , x T ) d x 1 . . . d x T = E x 0 ∼ q ( x 0 ) log E ( x 1 , . . . x T ) ∼ q ( x 1 , . . . , x T ∣ x 0 ) q ( x 1 , . . . , x T ∣ x 0 ) p ( x 0 , . . . , x T ) ≥ E x 0 ∼ q ( x 0 ) E ( x 1 , . . . x T ) ∼ q ( x 1 , . . . , x T ∣ x 0 ) log q ( x 1 , . . . , x T ∣ x 0 ) p ( x 0 , . . . , x T ) = E ( x 0 , x 1 , . . . x T ) ∼ q ( x 0 , x 1 , . . . , x T ) log q ( x 1 , . . . , x T ∣ x 0 ) p ( x 0 , . . . , x T ) = E ( x 0 , x 1 , . . . x T ) ∼ q ( x 0 , x 1 , . . . , x T ) [ log p ( x T ) + t = 1 ∑ T log q ( x t ∣ x t − 1 ) p ( x t − 1 ∣ x t ) ]
上式需要对整个联合分布q ( x 0 , . . . , x T ) q(x_0, ..., x_T) q ( x 0 , . . . , x T )
q ( x t ∣ x t − 1 ) = q ( x t ∣ x t − 1 , x 0 ) = q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) q(x_t|x_{t-1}) = q(x_t|x_{t-1}, x_0) = \frac{q(x_{t-1}|x_t, x_0) q(x_t|x_0)}{q(x_{t-1}|x_0)}
q ( x t ∣ x t − 1 ) = q ( x t ∣ x t − 1 , x 0 ) = q ( x t − 1 ∣ x 0 ) q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 )
从而似然函数的下界可进一步展开为:
E q ( x 0 , . . . , x T ) [ log p ( x T ) + ∑ t = 2 T log p ( x t − 1 ∣ x t ) q ( x t − 1 ∣ x t , x 0 ) q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) + log p ( x 0 ∣ x 1 ) q ( x 1 ∣ x 0 ) ] = E q ( x 0 , . . . , x T ) [ log p ( x T ) + ∑ t = 2 T log p ( x t − 1 ∣ x t ) q ( x t − 1 ∣ x t , x 0 ) + log q ( x 1 ∣ x 0 ) q ( x T ∣ x 0 ) + log p ( x 0 ∣ x 1 ) q ( x 1 ∣ x 0 ) ] = E q ( x 0 , . . . , x T ) [ log p ( x T ) q ( x T ∣ x 0 ) + ∑ t = 2 T log p ( x t − 1 ∣ x t ) q ( x t − 1 ∣ x t , x 0 ) + log p ( x 0 ∣ x 1 ) ] = ∫ q ( x 0 , x T ) log p ( x T ) q ( x T ∣ x 0 ) d x 0 d x T + ∫ q ( x 0 , x 1 ) log p ( x 0 ∣ x 1 ) d x 0 d x 1 + ∑ t = 2 T ∫ q ( x 0 , x t − 1 , x t ) log p ( x t − 1 ∣ x t ) q ( x t − 1 ∣ x t , x 0 ) d x 0 d x t − 1 d x t = − E q ( x 0 ) D K L ( q ( x T ∣ x 0 ) ∥ p ( x T ) ) + E q ( x 0 , x 1 ) log p ( x 0 ∣ x 1 ) − ∑ t = 2 T E q ( x 0 , x t ) D K L ( q ( x t − 1 ∣ x t , x 0 ) ∥ p ( x t − 1 ∣ x t ) ) = L T + L 0 + ∑ t = 2 T L t − 1 \begin{aligned}
&\mathbb{E}_{q(x_0, ..., x_T)} \left[ \log p(x_T) + \sum_{t=2}^T \log \frac{p(x_{t-1}|x_t)}{q(x_{t-1}|x_{t}, x_0)} \frac{q(x_{t-1}|x_0)}{q(x_t|x_0)} + \log \frac{p(x_0|x_1)}{q(x_1|x_0)} \right]\\
=&\mathbb{E}_{q(x_0, ..., x_T)} \left[ \log p(x_T) + \sum_{t=2}^T \log \frac{p(x_{t-1}|x_t)}{q(x_{t-1}|x_{t}, x_0)} + \log \frac{q(x_1|x_0)}{q(x_T|x_0)} + \log \frac{p(x_0|x_1)}{q(x_1|x_0)} \right]\\
=&\mathbb{E}_{q(x_0, ..., x_T)} \left[ \log \frac{p(x_T)}{q(x_T|x_0)} + \sum_{t=2}^T \log \frac{p(x_{t-1}|x_t)}{q(x_{t-1}|x_{t}, x_0)} + \log p(x_0|x_1) \right]\\
=&\int q(x_0, x_T)\log \frac{p(x_T)}{q(x_T|x_0)} dx_0 dx_T + \int q(x_0, x_1) \log p(x_0|x_1) dx_0 dx_1 \\
& + \sum_{t=2}^T \int q(x_0, x_{t-1}, x_t) \log \frac{p(x_{t-1}|x_t)}{q(x_{t-1}|x_{t}, x_0)} dx_0 dx_{t-1} dx_t \\
=&~ -\mathbb{E}_{q(x_0)} D_{KL} \Big(q(x_T|x_0) \Big\| p(x_T) \Big) + \mathbb{E}_{q(x_0, x_1)} \log p(x_0|x_1)\\
&- \sum_{t=2}^T \mathbb{E}_{q(x_0, x_t)} D_{KL} \Big(q(x_{t-1}|x_{t}, x_0) \Big\| p(x_{t-1}|x_t) \Big)\\
=& ~~~ L_T + L_0 + \sum_{t=2}^T L_{t-1}
\end{aligned} = = = = = E q ( x 0 , . . . , x T ) [ log p ( x T ) + t = 2 ∑ T log q ( x t − 1 ∣ x t , x 0 ) p ( x t − 1 ∣ x t ) q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) + log q ( x 1 ∣ x 0 ) p ( x 0 ∣ x 1 ) ] E q ( x 0 , . . . , x T ) [ log p ( x T ) + t = 2 ∑ T log q ( x t − 1 ∣ x t , x 0 ) p ( x t − 1 ∣ x t ) + log q ( x T ∣ x 0 ) q ( x 1 ∣ x 0 ) + log q ( x 1 ∣ x 0 ) p ( x 0 ∣ x 1 ) ] E q ( x 0 , . . . , x T ) [ log q ( x T ∣ x 0 ) p ( x T ) + t = 2 ∑ T log q ( x t − 1 ∣ x t , x 0 ) p ( x t − 1 ∣ x t ) + log p ( x 0 ∣ x 1 ) ] ∫ q ( x 0 , x T ) log q ( x T ∣ x 0 ) p ( x T ) d x 0 d x T + ∫ q ( x 0 , x 1 ) log p ( x 0 ∣ x 1 ) d x 0 d x 1 + t = 2 ∑ T ∫ q ( x 0 , x t − 1 , x t ) log q ( x t − 1 ∣ x t , x 0 ) p ( x t − 1 ∣ x t ) d x 0 d x t − 1 d x t − E q ( x 0 ) D K L ( q ( x T ∣ x 0 ) ∥ ∥ ∥ ∥ p ( x T ) ) + E q ( x 0 , x 1 ) log p ( x 0 ∣ x 1 ) − t = 2 ∑ T E q ( x 0 , x t ) D K L ( q ( x t − 1 ∣ x t , x 0 ) ∥ ∥ ∥ ∥ p ( x t − 1 ∣ x t ) ) L T + L 0 + t = 2 ∑ T L t − 1
上式中p ( x T ) p(x_T) p ( x T ) z \bm{z} z p ( x t − 1 ∣ x t ) p(x_{t-1}|x_t) p ( x t − 1 ∣ x t ) x 0 x_0 x 0 q ( x 0 ) q(x_0) q ( x 0 ) q ( x 0 , x t ) q(x_0, x_t) q ( x 0 , x t ) q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t, x_0) q ( x t − 1 ∣ x t , x 0 ) Lil’Log ),从而上述似然函数下界是可解的。
q ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x t − 1 ) q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) = N ( x t − 1 ; μ ( x t , x 0 ) , β ~ t I ) q(x_{t-1}|x_t, x_0) = q(x_t|x_{t-1}) \frac{q(x_{t-1}|x_0)}{q(x_t|x_0)} = \mathcal{N}(x_{t-1}; \mu(x_t, x_0), \tilde{\beta}_tI)
q ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x t − 1 ) q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) = N ( x t − 1 ; μ ( x t , x 0 ) , β ~ t I )
μ ( x t , x 0 ) = 1 − β t ( 1 − α t − 1 ) 1 − α t x t + α t − 1 β t 1 − α t x 0 , β ~ t = 1 − α t − 1 1 − α t β t \mu(x_t, x_0) = \frac{\sqrt{1-\beta_t}(1-\alpha_{t-1}) }{1-\alpha_t}x_t + \frac{\sqrt{\alpha_{t-1}}\beta_t}{1-\alpha_t}x_0, ~~~ \tilde{\beta}_t = \frac{1-\alpha_{t-1}}{1-\alpha_t}\beta_t
μ ( x t , x 0 ) = 1 − α t 1 − β t ( 1 − α t − 1 ) x t + 1 − α t α t − 1 β t x 0 , β ~ t = 1 − α t 1 − α t − 1 β t
事实上,β t \beta_t β t q ( x T ∣ x 0 ) q(x_T|x_0) q ( x T ∣ x 0 ) L T L_T L T L 0 L_0 L 0 L t − 1 L_{t-1} L t − 1 β \beta β p ( x t − 1 ∣ x t ) p(x_{t-1}|x_t) p ( x t − 1 ∣ x t ) β 1 = 1 0 − 4 , β T = 0.02 \beta_1=10^{-4}, \beta_T=0.02 β 1 = 1 0 − 4 , β T = 0 . 0 2 L t − 1 L_{t-1} L t − 1 Sohl-Dickstein et al. (2015) 中所构建的概率扩散模型框架已完成。
DDPM的主要贡献是通过重参数化,将对(条件)分布均值方差的预测转化为对噪声 的预测,因此名为去噪DPM。文章中选择固定方差Σ t = σ t 2 I \Sigma_t = \sigma^2_t I Σ t = σ t 2 I σ t 2 \sigma^2_t σ t 2 β t \beta_t β t β ~ t \tilde{\beta}_t β ~ t p ( x t − 1 ∣ x t ) = N ( x t − 1 ; μ ~ ( x t , t ; θ ) , σ t 2 I ) p(x_{t-1}|x_t) = \mathcal{N}(x_{t-1}; \tilde{\mu}(x_t, t; \bm{\theta}), \sigma_t^2 I) p ( x t − 1 ∣ x t ) = N ( x t − 1 ; μ ~ ( x t , t ; θ ) , σ t 2 I ) L t − 1 L_{t-1} L t − 1
L t − 1 = E q ( x 0 , x t ) [ 1 2 σ t 2 ∥ μ ( x t , x 0 ) − μ ~ ( x t , t ; θ ) ∥ 2 ] + C L_{t-1} = \mathbb{E}_{q(x_0, x_t)} \left[ \frac{1}{2\sigma^2_t} \left\|\mu(x_t, x_0) - \tilde{\mu}(x_t, t; \bm{\theta})\right\|^2\right] + C
L t − 1 = E q ( x 0 , x t ) [ 2 σ t 2 1 ∥ μ ( x t , x 0 ) − μ ~ ( x t , t ; θ ) ∥ 2 ] + C
其中μ ( x t , x 0 ) \mu(x_t, x_0) μ ( x t , x 0 ) q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q ( x t − 1 ∣ x t , x 0 ) μ ~ ( x t , t ; θ ) \tilde{\mu}(x_t, t; \bm{\theta}) μ ~ ( x t , t ; θ ) p ( x t − 1 ∣ x t ) p(x_{t-1}|x_t) p ( x t − 1 ∣ x t ) x t x_t x t x t ( x 0 , ϵ ) = α t x 0 + 1 − α t ϵ , ϵ ∼ N ( 0 , I ) x_t(x_0, \epsilon) = \sqrt{\alpha_t}x_0 + \sqrt{1-\alpha_t}\epsilon, ~~\epsilon \sim \small\mathcal{N}(0, I) x t ( x 0 , ϵ ) = α t x 0 + 1 − α t ϵ , ϵ ∼ N ( 0 , I ) x t ( x ~ 0 , ϵ ~ ) = α t x ~ 0 + 1 − α t ϵ ~ ( x t , t ; θ ) x_t(\tilde{x}_0, \tilde{\epsilon}) = \sqrt{\alpha_t}\tilde{x}_0 + \sqrt{1-\alpha_t}\tilde{\epsilon}(x_t, t; \bm{\theta}) x t ( x ~ 0 , ϵ ~ ) = α t x ~ 0 + 1 − α t ϵ ~ ( x t , t ; θ ) x ~ 0 \tilde{x}_0 x ~ 0 x 0 x_0 x 0 ϵ ~ ( x t , t ; θ ) \tilde{\epsilon}(x_t, t; \bm{\theta}) ϵ ~ ( x t , t ; θ ) ϵ \epsilon ϵ x t x_t x t x 0 , x ~ 0 x_0, \tilde{x}_0 x 0 , x ~ 0 x t x_t x t μ ( x t , x 0 ) \mu(x_t, x_0) μ ( x t , x 0 )
μ ( x t , x 0 ) = 1 1 − β t ( x t − β t 1 − α t ϵ ) μ ~ ( x t , t ; θ ) = 1 1 − β t ( x t − β t 1 − α t ϵ ~ ( x t , t ; θ ) ) \begin{aligned}
\mu(x_t, x_0) &= \frac{1}{\sqrt{1-\beta_t}}(x_t - \frac{\beta_t}{\sqrt{1-\alpha_t} }\epsilon)\\
\tilde{\mu}(x_t, t; \bm{\theta}) &= \frac{1}{\sqrt{1-\beta_t}}(x_t - \frac{\beta_t}{\sqrt{1-\alpha_t} }\tilde{\epsilon}(x_t, t; \bm{\theta}))
\end{aligned}
μ ( x t , x 0 ) μ ~ ( x t , t ; θ ) = 1 − β t 1 ( x t − 1 − α t β t ϵ ) = 1 − β t 1 ( x t − 1 − α t β t ϵ ~ ( x t , t ; θ ) )
其中x t x_t x t L t − 1 L_{t-1} L t − 1 ϵ \epsilon ϵ
L t − 1 = E x 0 , ϵ [ β t 2 2 σ t 2 ( 1 − β t ) ( 1 − α t ) ∥ ϵ − ϵ ~ ( x t ( x 0 , ϵ ) , t ; θ ) ∥ 2 ] + C L_{t-1} = \mathbb{E}_{x_0, \epsilon} \left[ \frac{\beta^2_t}{2\sigma_t^2 (1-\beta_t)(1-\alpha_t)} \left\|\epsilon - \tilde{\epsilon}\big(x_t(x_0, \epsilon), t; \bm{\theta}\big)\right\|^2 \right] + C
L t − 1 = E x 0 , ϵ [ 2 σ t 2 ( 1 − β t ) ( 1 − α t ) β t 2 ∥ ∥ ∥ ϵ − ϵ ~ ( x t ( x 0 , ϵ ) , t ; θ ) ∥ ∥ ∥ 2 ] + C
最终目标函数的核心为:
L = E x 0 ∼ q ( x 0 ) , ϵ ∼ N ( 0 , I ) ∥ ϵ − ϵ ~ ( x t ( x 0 , ϵ ) , t ; θ ) ∥ 2 \boxed{L = \mathbb{E}_{x_0 \sim q(x_0), \epsilon\sim\tiny \mathcal{N}(0,I)} \left\|\epsilon - \tilde{\epsilon}\big(x_t(x_0, \epsilon), t; \bm{\theta}\big)\right\|^2 }
L = E x 0 ∼ q ( x 0 ) , ϵ ∼ N ( 0 , I ) ∥ ∥ ∥ ϵ − ϵ ~ ( x t ( x 0 , ϵ ) , t ; θ ) ∥ ∥ ∥ 2
DDPM的训练过程可简单概括为:
对数据x 0 x_0 x 0 t ∼ Uniform ( { 1 , . . . , T } ) t\sim \small \text{Uniform}(\{1, ..., T\}) t ∼ Uniform ( { 1 , . . . , T } ) ϵ ∼ N ( 0 , I ) \epsilon\sim \small \mathcal{N}(0,I) ϵ ∼ N ( 0 , I )
∇ θ ∥ ϵ − ϵ ~ ( x t ( x 0 , ϵ ) , t ; θ ) ∥ 2 \nabla_\bm{\theta} \left\|\epsilon - \tilde{\epsilon}\big(x_t(x_0, \epsilon), t; \bm{\theta}\big)\right\|^2
∇ θ ∥ ∥ ∥ ϵ − ϵ ~ ( x t ( x 0 , ϵ ) , t ; θ ) ∥ ∥ ∥ 2
生成过程需由x T x_T x T
对x T ∼ N ( 0 , I ) x_T \sim \small \mathcal{N}(0, I) x T ∼ N ( 0 , I ) x T x_T x T
反向扩散:给定x t x_t x t p ( x t − 1 ∣ x t ) p(x_{t-1}|x_t) p ( x t − 1 ∣ x t ) x t − 1 x_{t-1} x t − 1 t = T , . . . , 1 t = T, ..., 1 t = T , . . . , 1 x t − 1 = 1 1 − β t ( x t − β t 1 − α t ϵ ~ ( x t , t ; θ ) ) + σ t ε x_{t-1} = \frac{1}{\sqrt{1-\beta_t}}\left(x_t - \frac{\beta_t}{\sqrt{1-\alpha_t}} \tilde{\epsilon}(x_t, t; \bm{\theta}) \right) + \sigma_t \varepsilon
x t − 1 = 1 − β t 1 ( x t − 1 − α t β t ϵ ~ ( x t , t ; θ ) ) + σ t ε
t > 1 t>1 t > 1 ε ∼ N ( 0 , I ) \varepsilon \sim \small \mathcal{N}(0, I) ε ∼ N ( 0 , I ) x 0 ( t = 1 ) x_0(t=1) x 0 ( t = 1 ) ε = 0 \varepsilon=0 ε = 0
Improved
DDIM
Improved DDPM
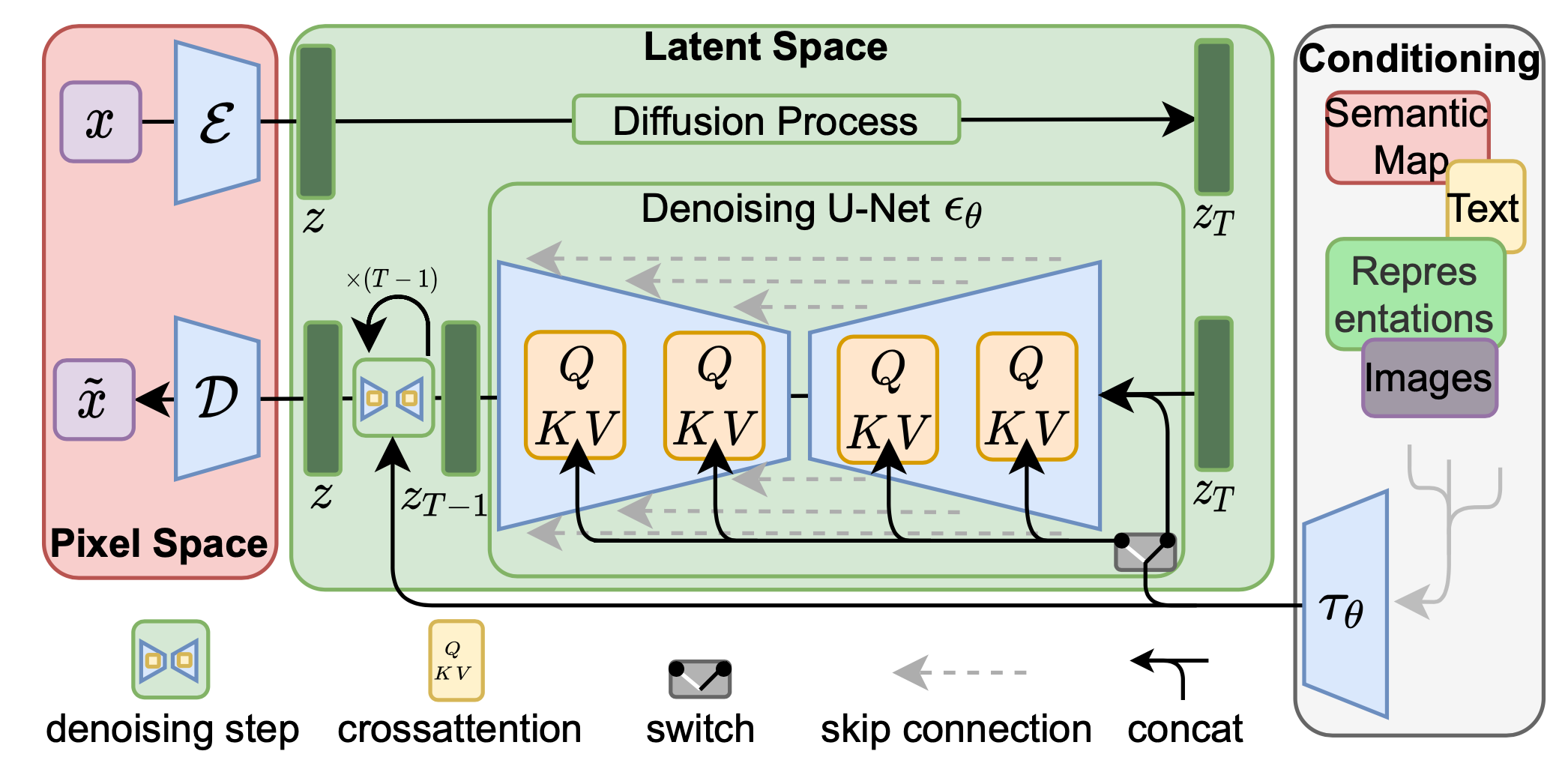
LDM τ θ ( y ) \tau_\bm{\theta}(y) τ θ ( y )
L = E x , y , ϵ ∥ ϵ − ϵ ~ ( z t ( z , ϵ ) , τ θ ( y ) , t ; θ ) ∥ 2 \boxed{L = \mathbb{E}_{x, ~y,~ \epsilon} \left\|\epsilon - \tilde{\epsilon}\big(z_t(z, \epsilon), \tau_\bm{\theta}(y), t ; \bm{\theta}\big)\right\|^2 }
L = E x , y , ϵ ∥ ∥ ∥ ϵ − ϵ ~ ( z t ( z , ϵ ) , τ θ ( y ) , t ; θ ) ∥ ∥ ∥ 2
https://en.wikipedia.org/wiki/Diffusion_model Deep Unsupervised Learning using Nonequilibrium Thermodynamics Denoising Diffusion Probabilistic Models
SDE视角下的扩散模型
GflowNets
探索(exploration)和开发(exploitation)
Wasserstein GAN Read-through: Wasserstein GAN 令人拍案叫绝的Wasserstein GAN 扩散模型之DDPM https://www.thepaper.cn/newsDetail_forward_8089082