信号分析：随机过程

广义平稳随机过程、各态历经性；匹配滤波；高斯过程、随机游走、泊松过程、马尔科夫链

随机过程基础

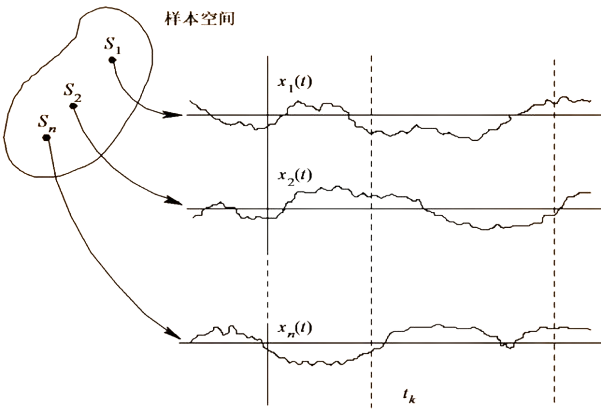
随机过程就是每刻取值都随机的过程。如上图所示：从纵向角度，对于固定的时间$t_k$，随机过程表现为随机变量$\mathbf{x}(t_k)$；而从横向角度，对于一系列时序观测，随机过程对应确定的时序函数$x(t)$，被称为样本函数或一次实现(relization)；在整体上，无数可能实现/样本函数所组成的系综/函数族(ensemble)才对应于随机过程$\mathbf{x}(t)$。

随机过程在某种程度上可理解为以“函数”为样本的随机变量，每次“试验”得到的不是一个数值，而是一系列随机数值所组成的函数(实现)。其随机性源自$\mathbf{x}$而非$t$，不同时刻对应不同的随机变量，而每次试验得到的具体实现$x(t)$是确定性的时序信号。

相关的一些符号介绍：

• $\mathbf{x}(t), \mathbf{y}(t)$：随机过程（或其在时刻$t$对应的随机变量）
• $\mathbf{x}(t_1), \mathbf{x}(t_2)$：随机过程在不同时刻所对应的随机变量
• $x(t), y(t)$：随机过程的一次具体试验/实现(relization)
• $x_1(t), x_2(t)$：同一随机过程的两次不同试验/实现
• $\{x_i(t)\}$：全部可能实现的集合，即系综(ensemble)
• $x(t_1), x(t_2)$：随机过程一次实现的不同时刻取值
• $x_1(t_1), x_2(t_2)$：随机过程不同实现在的不同时刻取值

从随机变量角度，最基本的是从统计上进行研究，获取确定性的统计量，为此需先引入描述随机过程的概率分布。任意时刻$t$，可定义分布函数$F(x; t) = P\{\mathbf{x}(t) \le x\}$，对应的概率密度为$f(x;t) = \frac{\partial F(x; t)}{\partial x}$。从事件频率角度理解，随机过程的每次实现都将得到一个关于时间的函数$x(t)$，重复$n$次实验将有$n$个不同函数$\{x_i(t)\}$，对每一时刻$t$计算函数值小于给定值$x$的频率就可近似得到分布函数$F(x; t)$。根据上述概率密度可计算随机过程的均值和方差：

$$\mu(t) = E\{ \mathbf{x}(t) \} = \int x(t) f(x; t) dx$$

$$\sigma^2(t) = E\left\{ \big[\mathbf{x}(t)-\mu(t)\big]^2 \right\} = \int \big[x(t)-\mu(t)\big]^2 f(x; t) dx$$

显然，一般情况下均值和方差会随时间变化。注意随机过程是关于时间的随机变量，而其均值和方差则是关于时间的确定性函数。

进一步的，对于随机过程中不同时刻的随机变量$\mathbf{x}(t_1), \mathbf{x}(t_2)$还可以定义联合分布，被称为二阶分布：$F(x_1, x_2; t_1, t_2) = P\{\mathbf{x}(t_1) \le x_1, \mathbf{x}(t_2) \le x_2\}$，对应的概率密度函数为$f(x_1, x_2; t_1, t_2) = \frac{\partial^2 F(x_1, x_2; t_1, t_2)}{\partial x_1 \partial x_2}$。相对的，任意时刻随机变量单独的分布被称为一阶分布，对二阶分布其中一个时刻的随机变量积分可得到另一时刻随机变量的分布(边际概率)。利用二阶分布可计算随机过程的自相关函数：

$$r_{\mathbf{xx}}(t_1, t_2) = E\big\{ \mathbf{x}(t_1)\mathbf{x}(t_2) \big\} = \iint x_1(t_1) x_2(t_2) f(x_1, x_2; t_1, t_2) dx_1 dx_2$$

类似的，还可以定义两个随机过程$\mathbf{x}(t), \mathbf{y}(t)$不同时刻的互相关函数：

$$r_{\mathbf{xy}}(t_1, t_2) = E\big\{ \mathbf{x}(t_1)\mathbf{y}(t_2) \big\} = \iint x(t_1) y(t_2) f(x, y; t_1, t_2) dx dy$$

在计算自相关/互相关前减去均值，可以得到对应的自协方差(autocovariance)$\gamma_{\mathbf{xx}}(t_1, t_2)$及协方差(covariance)$\gamma_{\mathbf{xy}}(t_1, t_2)$：

$$\gamma_{\mathbf{xx}}(t_1, t_2) = E\big\{ [\mathbf{x}(t_1) -\mu(t_1)][\mathbf{x}(t_2)-\mu(t_2)] \big\} = r_{\mathbf{xx}}(t_1, t_2) - \mu(t_1)\mu(t_2)$$

$$\gamma_{\mathbf{xy}}(t_1, t_2) = E\big\{ [\mathbf{x}(t_1) -\mu_\mathbf{x}(t_1)][\mathbf{y}(t_2)-\mu_\mathbf{y}(t_2)] \big\} = r_{\mathbf{xy}}(t_1, t_2) - \mu_\mathbf{x}(t_1)\mu_\mathbf{y}(t_2)$$

类似随机变量方差与协方差的关系$\text{var}\{\mathbf{x}\} = \text{cov}\{\mathbf{x}, \mathbf{x}\}$，随机过程方差与自协方差有$\sigma^2(t) = \gamma_{\mathbf{xx}}(t, t) = r_{\mathbf{xx}}(t, t) - \mu^2(t)$。

更进一步有$n$阶分布：$F(x_1, ..., x_n; t_1, ..., t_n) = P\{\mathbf{x}(t_1) \le x_1, ..., \mathbf{x}(t_n) \le x_n\}$及对应的概率密度$f(x_1, ..., x_n; t_1, ..., t_n)$。$n$阶分布对应随机过程$n$个不同时刻的联合分布，由高阶分布可以确定任意低阶分布(边际概率)。

最后，上面的讨论都仅限于对应实值函数的随机过程，对复值过程可通过两个实随机过程进行描述$\mathbf{z}(t) = \mathbf{x}(t) + i \mathbf{y}(t)$，并据此定义常用的统计量，唯一的区别的在于在计算二阶统计量(相关或协方差)时需取复共轭，如自相关为$r_\mathbf{zz}(t_1, t_2)= E\big\{ \mathbf{z}(t_1)\overline{\mathbf{z}(t_2)} \big\}$。

广义平稳过程

• (狭义)平稳过程：$\mathbf{x}(t)$与$\mathbf{x}(t+\epsilon)$具有相同的统计性质(分布)
  最严格的平稳过程要求任意阶分布都不随时间变化，可放宽到有限阶分布平稳。由于任意低阶分布都可由更高阶确定，因此$n$阶平稳，所有低于$n$阶的分布也都平稳。最高$n$阶分布不随时间变化的过程被称为$n$阶平稳过程。
  统计量上，一阶平稳过程均值、方差为常数，二阶平稳过程自相关函数只与时间差值有关$r_{\mathbf{xx}}(t_1, t_2) = E\{\mathbf{x}(t_1)\mathbf{x}(t_1)\}= E\{\mathbf{x}(t_1+\epsilon)\mathbf{x}(t_1+\epsilon)\} \equiv r_\mathbf{xx}(t_1-t_2)$。
• 广义平稳过程：均值为常数，且自相关函数只依赖时间差
  广义平稳(Wide Sense Stationary, WSS)过程，也被翻译为宽平稳过程。狭义平稳过程是从分布角度定义的，而广义平稳过程只限制了随机过程的一阶和二阶统计量，对具体分布则并没有要求。部分广义平稳过程可能连一阶平稳的要求都不满足，即虽然均值为常数(且自相关与具体时间无关)，但一阶分布却并不稳定，会随时间变化。比如$\mathbf{x}(t) = \cos(t+\bm{\theta})$, 其中$\bm{\theta}$服从均匀分布，样本空间为$\{0, \frac{1}{2}\pi, \pi, \frac{3}{2}\pi\}$。
• 联合平稳性：对两个随机过程$\mathbf{x}(t), \mathbf{y}(t)$可类似定义联合平稳性
  两个随机过程广义联合平稳被定义为：各自广义平稳，且互相关函数只依赖时间差。
• 其他平稳形式：周期平稳、渐近平稳、增量平稳、局部平稳

在时域中，广义平稳过程均值恒定，自相关函数只依赖时间差，并不直观。后面会介绍随机过程自相关函数与功率谱可构成傅里叶变换对，自相关只依赖时间差，即对应确定的功率谱。因此在频域视角下，广义平稳随机过程是频率成分固定、相位随机的过程，而非平稳过程则是频率成分随时间演化的过程。

广义平稳过程自相关性质：

• 只是时间差值的函数，记为$r_\mathbf{xx}(\tau)$
• 对实随机过程$\mathbf{x}(t)$，$r_\mathbf{xx}(\tau)$为实函数
• 偶对称 $r_\mathbf{xx}(\tau) = r_\mathbf{xx}(-\tau)$
• 零点值最大 $r_\mathbf{xx}(0) \ge |r_\mathbf{xx}(\tau)|$
• 零点值 $r_\mathbf{xx}(0) = r_\mathbf{xx}(t, t) = E\{\mathbf{x}^2(t)\} = \sigma^2 + \mu^2$
  其中$\mu^2$为直流功率，$\sigma^2$交流功率，$r_\mathbf{xx}(0)$则对应总的平均功率。
• $r_\mathbf{xx}(\tau) = \gamma_\mathbf{xx}(\tau) + \mu^2$ 任何时刻直流分量都是可拆分出来的
• 周期性 如果$r_\mathbf{xx}(T) = r_\mathbf{xx}(0)$，则$r_\mathbf{xx}(\tau)$和$\mathbf{x}(t)$都具有周期$T$
  反过来，如果$r_\mathbf{xx}(\tau)$和$\mathbf{x}(t)$不具有周期性，$r_\mathbf{xx}(0) > |r_\mathbf{xx}(\tau)|$将严格成立

对于广义联合平稳过程的互相关$r_\mathbf{xy}(\tau)$，不具有对称性，零点值也没有特殊意义。但$r_\mathbf{xy}(\tau) = r_\mathbf{yx}(-\tau)$，$r_\mathbf{xy}(\tau) \le \frac{1}{2}[r_\mathbf{xx}(0) + r_\mathbf{xx}(0)] \le \sqrt{r_\mathbf{xx}(0) r_\mathbf{yy}(0)}$

相关函数与相关系数
概率论中分析随机变量的相关性，通常会用到皮尔逊相关系数$\rho(\mathrm{X},\mathrm{Y}) = \frac{\mathrm{cov}(X, Y)}{\sigma_X \sigma_Y}$。虽然都是“相关”(correlate)，但显然两者有所区别。对于随机过程可引入作为时间函数的相关系数，相当于归一化的相关函数：减去均值乘积，除以方差乘积，取值范围变为$[-1, 1]$。对于广义平稳过程

$$\rho_{\mathbf{x},\mathbf{y}}(\tau) = \frac{\gamma_{\mathbf{x},\mathbf{y}}(\tau)}{\sigma_\mathbf{x} \sigma_\mathbf{x}} = \frac{r_{\mathbf{x},\mathbf{y}}(\tau) - \mu_\mathbf{x} \mu_\mathbf{y}}{\sigma_\mathbf{x} \sigma_\mathbf{y}}$$

随机向量与协方差矩阵
参照随机过程互相关的定义$r_\mathbf{xy}(t_1, t_2) = E\{ \mathbf{x}(t_1)\mathbf{y}(t_2) \}$，还可定义随机向量的互相关矩阵$R_\mathbf{XY} = E\{ \mathbf{XY}^T \}$，元素为随机向量元素两两相乘的期望$(R_\mathbf{XY})_{ij} = E\{ X_i Y_j \}$。相应的互协方差矩阵$K_\mathbf{XY} = E\Bigl\{ \bigl(\mathbf{X}-E\{\mathbf{X}\}\bigr)\bigl(\mathbf{Y}-E\{\mathbf{Y}\}\bigr)^T \Bigr\}$。

而通常说的，协方差矩阵一般是自协方差矩阵：

$$\Sigma = K_\mathbf{XX} = E\Bigl\{ \bigl(\mathbf{X}-E\{\mathbf{X}\}\bigr)\bigl(\mathbf{X}-E\{\mathbf{X}\}\bigr)^T \Bigr\}$$

从随机向量整体角度理解，协方差矩阵是随机向量的方差$\mathrm{var}\{\mathbf{X}\}$，是方差的高维推广；而从向量元素角度理解，协方差矩阵是不同向量分量(随机变量)间协变差构成的矩阵，这是其名称由来。实际上，考虑到对角元为分量方差，更准确的名称是“方差-协方差矩阵”。

进一步的，还可引入相关系数矩阵，即归一化的自相关矩阵，也可理解为归一化随机向量$\frac{\mathbf{X}-\bm{\mu}_\mathbf{X}}{\bm{\sigma}_\mathbf{X}} = \left(\frac{X_i-\mu_{X_i}}{\sigma_{X_i}}\right)$的自相关，对角元均为1，取值范围$[-1, 1]$。作为对比：

• 自相关矩阵 $R_\mathbf{XX} = E\{ \mathbf{XX}^T \}$
• 协方差矩阵 $\Sigma = R_\mathbf{XX} - E\{\mathbf{X}\}E\{\mathbf{X}\}^T$
• 相关(系数)矩阵 $C_\mathbf{XX} = \left(\frac{\Sigma_{ij}}{\sigma_{X_i}\sigma_{X_j}}\right)$

自相关矩阵和协方差矩阵都是对称矩阵，同时也都是半正定矩阵(特征值非负)。在Numpy中，一维序列相关为np.correlate，随机向量协方差为np.cov(输入的行对应单个随机变量，列对应单次观测)，而对应的相关系数为np.corrcoef。

各态历经性

前面都是从统计角度分析随机过程，作为无数具体实现(样本函数)组成的系综，实际中通常仅能获得随机过程的少数有限次、甚至单次的实现(如股价曲线)，从统计角度的分析并不现实。最好的情况是基于单次实现就可获取对系统整体统计性质的认知，这种优良特性被称为各态历经性/遍历性(Ergodicity)。这一概念源自统计物理，在随机过程中可简单描述为：系综期望(统计平均)等于具体实现的时间平均(ensemble average == time average)。基于各态历经性，对随机过程的描述可由(状态)空间变换到时间，获取单次试验数据即可展开分析，而无需进行大量重复试验。

$$\mu(t) = E[\mathbf{x}(t)] = \int x(t) f(x;t) dx ~~~ \leftrightarrow ~~~ \mu_x = ⟨x(t)⟩ = \lim_{T\rightarrow \infty} \frac{1}{2T}\int_{-T}^{T} x(t) dt$$

$$r_\mathbf{xx}(t, t+\tau) = E[\mathbf{x}(t)\mathbf{x}(t+\tau)] ~~~ \leftrightarrow ~~~ r_{xx}(\tau) = \lim_{T\rightarrow \infty} \frac{1}{2T}\int_{-T}^{T} x(t)x(t+\tau) dt$$

注意，各态历经性是与具体统计量直接相关联的，如均值各态历经、自相关/自协方差各态历经等。实际中各态历经通常默认指自相关各态历经(也自然暗含均值各态历经)。由于随机过程具体实现的时间平均$⟨x(t)⟩$是常数，均值各态历经要求随机过程均值$\mu(t) = E[\mathbf{x}(t)]$为常数；同时自相关的时间平均$r_{xx}(\tau)$只是时间差值的函数，自相关各态历经要求随机过程自相关函数$r_\mathbf{xx}(t, t+\tau)$只依赖时间差值。因此各态历经过程是广义平稳的，但反过来并不成立，平稳过程不一定各态历经。
注：上述结论是基于“系综平均等于时间平均”的要求得出的，但其实严谨的，数学上各态历经性仅要求系统“保测度(measure)”，即测度在时间演化下保持不变，或者说系统测度具有时间平移不变性。具体的对于均值各态历经，仅要求随机过程时间平均为常数，即任意实现的时间平均相等，并不要求该常数就是系综平均。因此，严格的各态经历与广义平稳是两个独立概念。

“各态历经”字面理解就是要每次实现都会遍历所有可能的状态。为直观的理解各态历经性，可将对随机变量的采样视为随机过程：逐次独立采样所构成的时间序列可理解为该随机过程的一次实现，而同时的无数次独立采样则对应随机过程系综的时间切片，显然前后两者具有相同的统计性质，即单次试验的时间平均等于系综平均。最简单的，一个色子的连续投掷与无数色子的同时投掷在统计上是没有区别的。

相对的，如果先后采样不独立，则采样过程就可能不再具有各态历经性，比如初始时刻取值是随机变量，但其后所有时刻取值都等于初始时刻值。这种情况下，每次实现显然无法遍历所有状态：随机过程具体实现的时间平均就等于初始时刻取值，是随机变量，而系统的系综平均则为初始时刻随机变量的均值，为固定值，因此不是各态历经的。事实上，该过程是平稳的，但非各态历经，类似的过程还有随机游走。

一般的，随机过程的时间平均应为随机变量(或过程)，对于均值和自相关/自协方差有：

$$\begin{aligned} \bm{\mu}_\mathbf{x} &= ⟨\mathbf{x}(t)⟩ = \lim_{T\rightarrow \infty} \frac{1}{T}\int_{-T/2}^{T/2} \mathbf{x}(t) dt\\ \bm{r}_\mathbf{x}(\tau) &= \big⟨\mathbf{x}(t)\mathbf{x}(t+\tau)\big⟩ = \lim_{T\rightarrow \infty} \frac{1}{T}\int_{-T/2}^{T/2} \mathbf{x}(t)\mathbf{x}(t+\tau) dt\\ \bm{\gamma}_\mathbf{x}(\tau) &= \big⟨[\mathbf{x}(t)-\bm{\mu}_\mathbf{x}][\mathbf{x}(t+\tau)-\bm{\mu}_\mathbf{x}]\big⟩ = \bm{r}_\mathbf{x}(\tau) - \bm{\mu}_\mathbf{x}^2 \end{aligned}$$

而各态历经则要求该随机变量为常数(或确定函数)，即：

$$\begin{aligned} \bm{\mu}_\mathbf{x} &= E\{\mathbf{x}(t)\} = \mu_x,\\ \bm{r}_\mathbf{x}(\tau) &= r_\mathbf{xx}(\tau) = r_{xx}(\tau),\\ \bm{\gamma}_\mathbf{x}(\tau) &= \gamma_\mathbf{xx}(\tau) = \gamma_{xx}(\tau) \end{aligned}$$

以均值各态历经为例，在统计上，这对应于：

$$E\{\mathbf{x}(t)\} = \bm{\mu}_\mathbf{x} = \mu_x, ~~~~ \text{Var}\{\bm{\mu}_\mathbf{x}\} = E\{[\bm{\mu}_\mathbf{x}- \mu_x]^2\} = E\{\bm{\mu}_\mathbf{x}^2\} - \mu_x^2 = 0$$

利用期望、极限及积分的可交换性(这里不讨论严格的数学要求)：

$$\begin{aligned} E\{\bm{\mu}_\mathbf{x}\} &= \lim_{T\rightarrow \infty} \frac{1}{T}\int_{-T/2}^{T/2} E\{\mathbf{x}(t)\} dt,\\ E\{\bm{\mu}_\mathbf{x}^2\} &= \lim_{T\rightarrow \infty} \frac{1}{T^2}\int_{-T/2}^{T/2}\int_{-T/2}^{T/2} E\{\mathbf{x}(t_1)\mathbf{x}(t_2)\} dt_1dt_2 \end{aligned}$$

即，为检验均值各态历经，不仅要考虑随机过程的均值$\mu(t) = E\{\mathbf{x}(t)\}$，还需要借助其自相关函数$r_\mathbf{xx}(t_1, t_2) = E\{\mathbf{x}(t_1)\mathbf{x}(t_2)\}$，而自相关各态历经则需要考虑四阶统计量的信息，这里不再讨论。广义平稳过程均值为常数，自相关函数仅依赖时间差值，容易证明$E\{\bm{\mu}_\mathbf{x}\} = E\{\mathbf{x}(t)\} = \mu_x$。$\text{Var}\{\bm{\mu}_\mathbf{x}\}$ 处理起来相对复杂，但可以证明，对于广义平稳的随机过程，其均值各态历经的充要条件是：

$$\lim_{T\rightarrow \infty} \frac{1}{T}\int_{-T/2}^{T/2} \gamma_\mathbf{xx}(\tau) d\tau = 0 ~~~~~ \text{\small 或} ~~~~~ \lim_{T\rightarrow \infty} \frac{1}{T}\int_{-T/2}^{T/2} r_\mathbf{xx}(\tau) d\tau = \mu_x^2$$

进一步，可证明以下情况是符合上述条件的，是广义平稳过程均值各态历经的充分条件：

$$\lim_{\tau\rightarrow \infty} \gamma_\mathbf{xx}(\tau) = 0 ~~~~~ \text{\small 或} ~~~~~ \lim_{\tau\rightarrow \infty} r_\mathbf{xx}(\tau) = \mu^2$$

直观的，上述条件要求随机过程，在间隔时间足够长时，前后随机变量趋向不相关，这其实是一个很合理的要求。

Stochastic Processes

$$\bm{\mu}_T = \frac{1}{T}\int_{-T/2}^{T/2} \mathbf{x}(t) dt, ~~~ \bm{\mu}_\mathbf{x} = \lim_{T\rightarrow\infty} \frac{1}{T}\int_{-T/2}^{T/2} \mathbf{x}(t) dt = \lim_{T\rightarrow\infty} \bm{\mu}_T$$

$$\begin{aligned}\text{Var}\{\bm{\mu}_T\} =& E\{ \bm{\mu}_T^2\} -E^2\{\bm{\mu}_T\}\\ =& \int\int \mu_{x_{1T}}\mu_{x_{2T}} f(x_1, x_2) dx_1 dx_2 - \left(\int \mu_{x_T} f(x) dx \right)^2 \\ =& \int\int dx_1 dx_2 \int_{-T/2}^{T/2}\frac{dt_1}{T} \int_{-T/2}^{T/2} \frac{dt_2}{T} ~ x_1(t_1)x_2(t_2) f(x_1, x_2; t_1, t_2) \\ &-\int dx_1 \int_{-T/2}^{T/2}\frac{dt_1}{T} ~ x_1(t_1)f(x_1; t_1) \int dx_2 \int_{-T/2}^{T/2} \frac{dt_2}{T} ~ x_2(t_2) f(x_2; t_2)\\ =& \int_{-T/2}^{T/2}\frac{dt_1}{T} \int_{-T/2}^{T/2} \frac{dt_2}{T} ~ r_{\mathbf{xx}}(t_1, t_2) - \left(\int_{-T/2}^{T/2} \frac{dt}{T} \mu_x(t)\right)^2 \end{aligned}$$

对于广义平稳过程，$r_{\mathbf{xx}}(t_1, t_2) = r_{\mathbf{xx}}(t_1-t_2), ~ \mu_x(t) = \mu_x$：

$$\begin{aligned} \text{Var}\{\bm{\mu}_T\} =& \frac{1}{T^2}\int_{-T/2}^{T/2} \int_{-T/2}^{T/2} dt_1dt_2 ~ r_{\mathbf{xx}}(t_1-t_2) - \mu_x^2\\ =& \frac{1}{T^2}\int_{-T/2}^{T/2}dt \int_{-\frac{T}{2}-t}^{\frac{T}{2}-t} d\tau ~ \gamma_{\mathbf{xx}}(\tau)\\ =& \frac{1}{T^2}\int_{0}^{T}dt \int_{-t}^{T-t} d\tau ~ \gamma_{\mathbf{xx}}(\tau)\\ =& \frac{1}{T^2} \left(\int_{-T}^{0}d\tau ~ \gamma_{\mathbf{xx}}(\tau) \int_{-\tau}^{T} dt + \int_{0}^{T}d\tau ~ \gamma_{\mathbf{xx}}(\tau) \int_{0}^{T-\tau} dt\right)\\ =& \frac{1}{T^2} \int_{-T}^{T}d\tau ~ \bigl(T-|\tau|\bigr) ~ \gamma_{\mathbf{xx}}(\tau)\\ =& \frac{1}{T^2} \int_{-T}^{T}d\tau ~ \left(\int^{T}_{|\tau|} dt\right) ~ \gamma_{\mathbf{xx}}(\tau)\\ =& \frac{1}{T^2} \int_{0}^{T} dt \int_{-t}^{t} d\tau ~ \gamma_{\mathbf{xx}}(\tau) \\ \lim_{T\rightarrow \infty} \frac{1}{T}\int_{-T/2}^{T/2} & \gamma_\mathbf{xx}(\tau) d\tau = 0 \\ \Leftrightarrow& \forall \epsilon>0, ~ \exists T_0, ~ \text{for} ~ t>T_0, \left|\frac{1}{2t}\int_{-t}^{t} \gamma_\mathbf{xx}(\tau) d\tau\right| < \epsilon\\ \Leftrightarrow& \forall \epsilon>0, ~ \exists T_0, ~ \text{for} ~ t>T_0, \left|\int_{-t}^{t} \gamma_\mathbf{xx}(\tau) d\tau\right| < 2t\epsilon\\ \text{Var}\{\bm{\mu}_T\} =& \frac{1}{T^2} \left( \int_{0}^{T_0} dt \int_{-t}^{t} d\tau ~ \gamma_{\mathbf{xx}}(\tau) + \int_{T_0}^{T} dt \int_{-t}^{t} d\tau ~ \gamma_{\mathbf{xx}}(\tau) \right)\\ \le& \frac{1}{T^2} \int_{0}^{T_0} dt \int_{-t}^{t} d\tau ~ |\gamma_{\mathbf{xx}}(\tau)| + \frac{1}{T^2} \int_{T_0}^{T} dt \left|\int_{-t}^{t} d\tau ~ \gamma_{\mathbf{xx}}(\tau)\right|\\ \le& \frac{1}{T^2} \int_{0}^{T_0} dt \int_{-t}^{t} d\tau ~ \gamma_{\mathbf{xx}}(0) + \frac{1}{T^2} \int_{T_0}^{T} 2t\epsilon ~ dt\\ =& \frac{T_0^2}{T^2} \gamma_{\mathbf{xx}}(0) + \frac{T^2-T_0^2}{T^2}\epsilon \end{aligned}$$

$$\forall \epsilon>0, ~ \text{Var}\{\bm{\mu}_\mathbf{x}\} = \lim_{T\rightarrow\infty} \text{Var}\{\bm{\mu}_T\} \le \epsilon ~~~ \Rightarrow ~~~ \text{Var}\{\bm{\mu}_\mathbf{x}\}=0$$

其他特殊过程

随机过程$\mathbf{x}(t)$在时刻$t$的概率分布$F(x; t)$是依赖于时间的，其划分也依赖于统计性质。

• 两个随机过程的正交、独立和不相关：
  • 不相关：不同时刻互协方差为零 $\forall t_1 \neq t_2, \gamma_\mathbf{xy}(t_1, t_2)=0$
    $~~~~r_\mathbf{xy}(t_1, t_2)=\mu_\mathbf{x}(t_1)\mu_\mathbf{y}(t_2)$
  • 正交：不同时刻互相关为零 $\forall t_1 \neq t_2, r_\mathbf{xy}(t_1, t_2)=0$
  • 独立：联合分布为逐点分布之积
    $\small \forall n, m, f(x_1, ..., x_n, y_1, ..., y_m; t_1, ..., t_n, t'_1, ..., t'_m ) = \prod_l f(x_k; t_k)\prod_l f(y_l; t'_l)$
• 类似的，根据自相关/自协方差可定义单个随机过程的不相关、正交与独立等概念
• 不相关/正交/独立增量过程：增量$\forall t_k,\mathbf{x}(t_k)\text{-}\mathbf{x}(t_{k+1})$为不相关/正交/独立过程
• 独立同分布(i.i.d.)过程：$\forall t, f(x; t)$ 相同且独立，属于严格平稳过程，常用于加性噪声的描述模型
• 高斯过程：$\forall n, f(x_1, ..., x_n; t_1, ..., t_n)$为正态分布
  注意高斯过程要求任意阶分布为正态分布，而不仅仅是一阶分布$f(x;t)$为正态分布。高斯过程的统计性质完全由其均值$\mu(t)$和自相关$r_\mathbf{xx}(t_1, t_2)$确定。

相关与功率谱

对于确定性函数，可通过傅里叶变换进行频域分解，而随机过程可视为无数具体实现组成的系综，原则上可以对其具体的实现进行傅里叶变换。但由于任意$t$，$\mathbf{x}(t)$为随机变量，因此大部分实现在$t\rightarrow\infty$时并不会趋于0，能量发散，也就不能进行傅里叶变换。

功率谱定义

为获取频谱可参照确定性函数的功率谱，针对随机过程的具体实现定义功率谱，但一般地该功率谱是随机的，不同实现的功率谱不同，需进一步对其求期望：

$$S(f) = \lim_{T\rightarrow\infty} \frac{1}{T} E\left\{ |\mathbf{X}_T(f)|^2 \right\}$$

在实际计算上，原则上可进行大量重复试验，对于每次试验得到的具体信号，截取有限时间区间计算功率谱$\frac{1}{T} |X_T(f)|^2$，并将所有试验得到功率谱求平均(系综期望)。下面会看到，对于各态历经过程，功率谱是确定的，所有实现功率谱相同。

除了分析随机过程的具体实现，另一个角度是分析随机过程的统计量，后者是确定性的函数。具体的，对于广义平稳过程，其均值为常数，没有分析的价值，而自相关作为时间差的函数，根据维纳-辛钦定理(Wiener–Khinchin theorem)有：

$$r_\mathbf{xx}(\tau) = E\big\{ \mathbf{x}(t)\mathbf{x}(t+\tau) \big\} = \int S(f) e^{i 2 \pi f \tau} df = \mathcal{F}^{-1}\{ S(f) \}$$

即对于广义平稳过程的自相关函数，存在频域的对应$S(f)$，为随机过程的功率谱：

$$\boxed{S(f) = \mathcal{F}\{ r_\mathbf{xx}(\tau) \} = \int r_\mathbf{xx}(\tau) e^{-i 2 \pi f \tau} d\tau}$$

上述关系对所有广义平稳过程成立，而对于自相关各态历经过程有$r_\mathbf{xx}(\tau) = r_{xx}(\tau)$，即随机过程的自相关可由单次试验的时间平均自相关得到，从而：

$$\begin{aligned} S(f) = \mathcal{F}\{ r_\mathbf{xx}(\tau) \} &= \mathcal{F}\{ r_{xx}(\tau) \} \\ &= \mathcal{F}\left\{ \lim_{T\rightarrow \infty} \frac{1}{T}\int_{-T/2}^{T/2} x(t)x(t+\tau) dt \right\}\\ &= \lim_{T\rightarrow \infty} \frac{1}{T} ~ \mathcal{F}\left\{ x_T(t) \star x_T(t)\right\}\\ &= \lim_{T\rightarrow \infty} \frac{1}{T} ~ |X_T(f)|^2 \end{aligned}$$

基于自相关各态历经，计算随机过程的功率谱$\mathcal{F}\{ r_\mathbf{xx}(\tau) \}$被转变为计算单次实现的功率谱$\mathcal{F}\{ r_{xx}(\tau) \} = \lim_{T\rightarrow \infty} \frac{1}{T} ~ |X_T(f)|^2$。

功率谱为实对称函数$S(-f) = S(f)$，且取值非负$S(f) \ge 0$。从能量或功率角度，显然功率谱需要是非负的，但是仅从FT角度该如何理解：$r_\mathbf{xx}(\tau)$不必非负，除了对称实函数外特殊在哪，为什么FT后非负？反过来说，满足什么条件的函数FT后一定非负，似乎是只有自相关函数具有这种性质，FT后会变为函数与自身共轭积(相关定理)。那么自相关函数在数学上的特殊性是什么，任意的函数满足什么条件，可作为另一个函数的自相关？这个问题其实并不简单，答案是正定性，正定函数是作为自相关函数的充要条件。其定义为对任意的$x_1, ..., x_n \in \R$，由$f(x_i-x_j)$构成的矩阵是半正定的，这很难验证，但博赫纳定理表明函数正定与傅里叶变换非负相对应。

对功率谱积分对应随机过程平均功率 $r_\mathbf{xx}(0) = E\left\{ \mathbf{x}^2(t) \right\} = \int S(f) df$，对均值为零的信号，反映的就是信号的方差$\sigma^2$。反过来，对自相关函数的积分对应直流分量，$S(0) = \int r_\mathbf{xx}(\tau) d\tau = \mu^2\delta(f)$。这个要如何证明？？为什么信号的均值就是直流分量，如何建立自相关积分与均值的联系，要利用各态历经性吗？

最后，对于广义联合平稳的两个随机过程，基于互相关函数可定义互功率谱。互功率谱并不一定为实函数$S_\mathbf{xy}(-f) = \overline{S_\mathbf{xy}(f)} = S_\mathbf{yx}(f)$。

自相关与功率谱的直观理解

数学上，自相关为间隔$\tau$的随机变量相乘的期望$r_\mathbf{xx}(\tau) = E\big\{ \mathbf{x}(t)\mathbf{x}(t+\tau) \big\}$。广义平稳过程均值为常数，即前后两者之和期望恒定，相乘的期望越大，则两者大致越接近。同时广义平稳过程自相关与时间无关，意味这种相似对随机过程所有时刻同时成立。因此自相关反映的是整个随机过程在平移$\tau$前后的相似性，即在不同时间尺度上趋势的一致性。

$r_\mathbf{xx}(\tau)$在越小$\tau$取值大，代表随机过程在越短的时间尺度上具有相似性，从而随机波动越剧烈(频率高)；而$r_\mathbf{xx}(\tau)$在越大的$\tau$上保持较大值，则随机在越长的时间尺度上保持相关性，随机过程变化越缓慢(频率低)。事实上考虑到自相关与功率谱构成傅里叶变换对，自相关与功率谱的延展程度(衰减速度)是反相关的。

均值为0时$\lim_{\tau\rightarrow \infty} r_\mathbf{xx}(\tau)=0$，同时自相关函数对称且$r_\mathbf{xx}(0) \ge |r_\mathbf{xx}(\tau)|$，尤其是对于非周期性信号，大于号严格成立。因此自相关函数通常呈现为零点最高，向两侧衰减的形式，具体值可正可负，所以可能存在震荡。而模值衰减的快慢反映了随机过程内部关联程度，衰减越快关联性越弱，也意味着信号随时间波动越剧烈(频率高)，反之则信号震荡越缓慢(频率低)。事实上
极端情况，前后完全不相关的白噪声，只有零点处取值非零；而完全相关的直流信号，自相关为恒值。

直观地，假设$\mathbf{x}(t)$为平稳随机过程，$\mathbf{y}(t)$由前者经时间压缩后得到，因此随机震荡会更为频繁。考虑到一阶平稳过程要求分布$f(x;t)$与时间无关，两个随机过程在一阶分布上完全相同。而在自相关上，$\mathbf{x}(t)$波动相对平稳，意味着对于小的时间差$\tau$，前后随机变量间具有相对更高的相关性，自相关的期望值也会更大。最终，功率谱在不同时间差值$\tau$的取值，反映出随机过程$\mathbf{x}(t)$震荡变化的快慢程度。

事实上，对于随机过程，自相关函数能够检测出原始信号内部蕴藏的周期组分。以初始相位随机的正弦波动为例，$\mathbf{x}(t)=\sin(\omega t + \bm{\phi})$，$\bm{\phi}$为$[0, 2\pi]$的均匀分布，大量初始相位随机的周期性随机信号叠加看似白噪声，但只要做自相关就可将周期性显现出来。

功率谱估计

平稳随机过程自相关函数是确定的，相应的功率谱也是确定的，但现实中观测数据是有限的，无法得到完整的自相关函数，只能用有限的数据对目标功率谱进行估计。具体方法上分两大类：以傅里叶变换为基础、非参数化的经典谱估计，以及以参数化模型为基础的现代谱估计。

经典谱估计中，观测数据之外直接视为零(或理解为周期性延拓)，受限于数据长度，频率分辨率有限，且存在偏置(谱泄露)。而考虑到数据中的随机噪声，经典谱估计还存在较大的方差，需要专门措施来补救。现代谱估计的出现点是基于数据内部关联性建立模型，合理外推，打破数据长度的限制，改善谱估计的分辨率和方差，最常见的是自回归AR模型。

经典谱估计：以FT为基础、非参数化、线性

• 直接法：周期图法及其改进
  • 周期图(Periodogram)：$\frac{1}{N f_s}\left|X_k\right|^2$ 对应数据的周期性延拓
  • 平均周期图(Bartlett’s method)：对数据切片，功率谱求平均
    对于随机过程，简单的周期图法得到的功率谱存在较大随机波动，平均周期图法将数据分段，之后分别计算功率谱并求平均(对应于数据折叠延拓)。数据切片牺牲了一定频率分辨率，但通过求平均，也减少了谱估计的波动性(方差)。
  • 加窗平均周期图(Welch’s method)：对数据片段加窗，允许重叠
    平均周期图直接切分数据，相当于对数据加矩形窗，存在较大频谱泄露(偏置)。Welch法通过使用其它窗口函数，改善频谱泄露，降低谱估计的偏置。由于窗函数会压低边缘数据，作为补偿Welch在数据分段时允许一定程度重叠。
  • 多窗口法(Multitaper method, MTM)：多个(正交)窗口，功率谱求平均
    多窗法是对完整数据应用一系列正交窗口，分别计算功率谱并求平均，以减低功率谱估计的波动(方差)和谱泄露(偏置)。虽然使用了完整数据，但相对简单周期图，多窗口法同样会降低频率分辨率。
  • 非均匀采样：Lomb-Scargle周期图
    受观测条件限制，现实数据经常存在采样不规律或数据缺失的情况，此时周期图法无法直接使用，除了对数据进行插值外，也可使用Lomb-Scargle周期图，对各频率成分引入不同时延，并将正弦和余弦系数分开加权。
• 间接法：自相关方法(Blackman-Tukey method)
  自相关函数是对称实函数，DFT只需要计算正频率的实部(1/4的计算量)，而通过对自相关函数加窗还可进一步减少计算量，这些计算上的优势使得BT法成为FFT普及前较常见的谱估计方法，不过现在更常用的是简单直接的周期图法。

现代谱估计：基于模型、(半)参数化、非线性
最常见的是将数据视为白噪声经过线性滤波得到的信号，比如移动平均MA模型将信号建模为输入白噪声的移动平均，自回归AR模型则将信号建模为自身的移动平均，ARMA是两者结合。功率谱密度$S(f; \theta_1, \ldots , \theta_p)$完全由模型参数决定，确定了参数就得到了谱密度。

无偏估计与一致估计
假设样本统计量$\hat{\mu}$为整体统计量$\mu$的估计，$\hat{\mu}$本身是随机变量：均值$E\{\hat{\mu}\}$(不一定等于$\mu$)，方差$\sigma_{\hat{\mu}}^2 = E\{(\hat{\mu} - E\{\hat{\mu}\})^2\} = E\{\hat{\mu}^2\} - E\{\hat{\mu}\}^2$。估计量$\hat{\mu}$相对真值$\mu$的偏置记为$b = \mu-E\{\hat{\mu}\}$，平均平方误差${\rm MSE}(\hat{\mu}) = E\{(\hat{\mu} - \mu)^2\} = b^2 + \sigma_{\hat{\mu}}^2$。

若$b=0, E\{\hat{\mu}\} = \mu$，称$\hat{\mu}$为$\mu$的无偏估计；若${\rm MSE}(\hat{\mu}) = 0$，称$\hat{\mu}$为$\mu$的一致估计。此外，当样本统计量依赖样本数$N$，若$\lim_{N\rightarrow\infty} E\{\hat{\mu}_N\} = \mu$，称$\hat{\mu}_N$为$\mu$的渐进无偏估计；若$\lim_{N\rightarrow\infty} {\rm MSE}(\hat{\mu}_N) = 0$，称$\hat{\mu}_N$为$\mu$的渐进一致估计。

自相关函数估计
对于各态历经的随机过程，自相关函数：

$$r_\mathbf{xx}(\tau) = E[\mathbf{x}(t)\mathbf{x}(t+\tau)] = r_{xx}(\tau) = \lim_{T\rightarrow \infty} \frac{1}{2T}\int_{-T}^{T} x(t)x(t+\tau) dt$$

对于离散随机过程：

$$r_\mathbf{xx}[k] = r_{xx}[k] = \lim_{N\rightarrow \infty} \frac{1}{N}\sum_{n=0}^{N-1} x[n]x[n+k] = \lim_{N\rightarrow \infty} E\{\mathbf{r}_N[k]\}$$

其中$\mathbf{r}_N[k]$是基于有限长随机过程对自相关函数的估计：

$$\mathbf{r}_N[k] = \frac{1}{N}\sum_{n=0}^{N-1} \mathbf{x}[n]\mathbf{x}[n+k], ~~ |k| \le N-1$$

注意，这里会出现指标越界，此时值取零(补零延拓)，等价的也可表示为：

$$\mathbf{r}_N[k] = \frac{1}{N}\sum_{n=0}^{N-|k|-1} \mathbf{x}[n]\mathbf{x}[n+|k|], ~~ |k| \le N-1$$

对上述表达式求期望有：

$$E\{\mathbf{r}_N[k]\} = \frac{1}{N}\sum_{n=0}^{N-|k|-1} E\{\mathbf{x}[n]\mathbf{x}[n+|k|]\} = \frac{N-|k|}{N} r_\mathbf{xx}[k], ~~ |k| \le N-1$$

可见$\mathbf{r}_N[k]$是自相关函数的有偏估计，但$\lim_{N\rightarrow\infty}\mathbf{r}_N[k] = r_\mathbf{xx}[k]$，因此是渐进无偏的。而根据上面的结果，可以引入$r_\mathbf{xx}[k]$的无偏估计：

$$\mathbf{r}'_N[k] = \frac{1}{N-|k|}\sum_{n=0}^{N-|k|-1} \mathbf{x}[n]\mathbf{x}[n+|k|], ~~ |k| \le N-1$$

但注意$\sigma^2_{\mathbf{r}'_N} = \left(\frac{N}{N-|k|}\right)^2\sigma^2_{\mathbf{r}_N}$，即估计的方差增大了。

自相关法频谱估计

$$\mathbf{S}_N[k] = \mathcal{F}\{ \mathbf{r}_N[m]\}$$

$$E\{\mathbf{S}_N[f_k]\} = \mathcal{F}\left\{ E\{\mathbf{r}_N[m]\}\right\} = \mathcal{F}\left\{ \frac{N-|m|}{N} r_\mathbf{xx}[m]\right\}, ~~ |m| \le N-1$$

$\mathbf{r}_N[k]$对$r_\mathbf{xx}[k]$估计局限于$\small [-(N-1), N-1]$区间，定义窗口函数：

$$w_N[m] = \begin{cases} \frac{N-|m|}{N} & \text{if} ~~ |m| \le N-1\\ 0 & \text{others} \end{cases}$$

$$E\{\mathbf{S}_N[f_k]\} = \mathcal{F}\left\{w_N[m] r_\mathbf{xx}[m]\right\} = \frac{1}{f_s} F_N\left(\frac{2\pi f}{f_s}\right)*S(f), ~~~ f\in[-\frac{f_s}{2}, \frac{f_s}{2})$$

注意这里$S(f)$需要是有限带宽的，限制在$[-\frac{f_s}{2}, \frac{f_s}{2})$区间，因为如果频率超过Nyquist频率，频谱将出现混叠，无论如何也无法正确估计原始频谱。$w_N[m]$其实就是三角窗，而$F_N(f)$为离散三角窗的傅里叶变换，被称为费耶尔核(Fejer Kernel)$F_N(x)=\frac{\sin^2(\frac{N}{2} x)}{N\sin^2(\frac{1}{2}x)}$，是以$2\pi$为周期的函数，对应于$\rm sinc^2$的折叠延拓。

类似的，基于自相关的无偏估计$\mathbf{r'}_N[m]$有：

$$E\{\mathbf{S'}_N[k]\} = \mathcal{F}\{ w'_N[m] r_\mathbf{xx}[m]\} = \frac{1}{f_s} D_N\left(\frac{2\pi f}{f_s}\right)*S(f), ~~~ f\in[-\frac{f_s}{2}, \frac{f_s}{2})$$

其中$w'_N[m]$为$\small [-(N-1),N-1]$区间的矩形窗，$D_N(f)$为离散矩形窗的傅里叶变换，被称为狄利克雷核(Dirichlet Kernel)$D_N(x)=\frac{\sin(\frac{2N+1}{2}x)}{\sin(\frac{1}{2}x)}$，也是以$2\pi$为周期的函数，对应于$\rm sinc$的折叠延拓。该估计的一个缺陷在于矩形窗傅里叶变换有负值，导致功率谱估计也会出现负值，这显然是不合理的，因此较少使用。不过无偏估计的$\mathbf{r'}_N[m]$可作为对自相关函数使用其他窗口函数的基础。

两种谱估计都是有偏的，但当$N\rightarrow\infty$时，$F_N(f)$和$D_N(f)$都趋向周期$2\pi$的狄拉克梳，从而谱估计趋向于$S(f), f\in[-\frac{f_s}{2}, \frac{f_s}{2})$，都是渐进无偏的。

周期图法 v.s. 自相关法

$$\begin{aligned} \mathbf{S}_N^{(P)}[k] &= \frac{1}{Nf_s} \left|\sum_{n=0}^{N-1} \mathbf{x}_n e^{-i \frac{2\pi k}{N} n}\right|^2 = \frac{1}{Nf_s} \sum_{p=0}^{N-1}\sum_{q=0}^{N-1} \overline{\mathbf{x}_p e^{-i \frac{2\pi k}{N} p}} \mathbf{x}_q e^{-i \frac{2\pi k}{N} q}\\ &= \frac{1}{Nf_s} \sum_{p=0}^{N-1}\sum_{q=0}^{N-1} \mathbf{x}_p \mathbf{x}_q e^{-i \frac{2\pi k}{N} (q-p)}\\ &= \frac{1}{f_s} \sum_{m=-(N-1)}^{N-1} \frac{1}{N}\sum_{p=0}^{N-|m|-1} \mathbf{x}_p \mathbf{x}_{p+|m|} ~~ e^{-i \frac{2\pi k}{N} m}\\ &= \frac{1}{f_s} \sum_{m=-(N-1)}^{N-1} \mathbf{r}_N[m] ~ e^{-i \frac{2\pi k}{N} m}\\ &= \mathcal{F}\{\mathbf{r}_N[m]\} = \mathbf{S}_N[k] \end{aligned}$$

对连续谱$S(f)=\int r(\tau) e^{-i2\pi f \tau} d\tau$，上式中相关函数离散傅里叶变换中出现的$\frac{1}{f_s}$对应这里的$d\tau$。可以看到周期图法与自相关法是等价的。

当然这种“等价”是有条件的。一方面，长度$2N+1$的自相关序列直接DFT，频率采样点是$\frac{f_s}{2N+1}$，也不同于周期图法中的$\frac{f_s}{N}$。注意频率分辨率上限受限于采样时间，即窗函数引入的频谱展宽$F_N(f)$，这里只是频点更多，并不能提高频谱的分辨率。另一方面，实际自相关计算中会对自相关序列加窗：

$$\mathbf{S}_N[k] = \frac{1}{f_s} \sum_{m=-(M-1)}^{M-1} \mathbf{r}_N[m] ~ e^{-i \frac{2\pi k}{N} m}$$

这里$\small M<N-1$，限制了相关的延迟量，通过牺牲频率分辨率(由$\frac{f_s}{N}$变为$\frac{f_s}{M}$)，实现功率谱的平滑，缓解信号截断造成的频泄露。直观理解，由于数据长度有限，当$m$取值较大时，计算$\mathbf{r}_N[m]$所用的数据量很少，波动较大，极端情况$\mathbf{r}_N[N-1] = \frac{1}{N}x[0]x[N-1]$。因此降低$m$较大部分自相关函数的贡献(加窗)，有助于降低频谱整体的不确定性。最终，自相关功率谱估计的期望为：

$$E\{\mathbf{S}_N[k]\} = S(f)*\frac{1}{f_s} F_N\left(\frac{2\pi f}{f_s}\right)*\frac{1}{f_s}D_M\left(\frac{2\pi f}{f_s}\right), ~~~ f\in[-\frac{f_s}{2}, \frac{f_s}{2})$$

在$\small N\rightarrow \infty, M\rightarrow \infty$时才是渐进无偏估计。而谱估计的方差$\sigma^2_{\mathbf{S}_N} \sim \frac{M}{N} S^2(f)$，显然随$M$减小方差减小，但另一方面随$M$减小分频率辨率会变差，偏置也会增强。渐进一致估计需要$M, \frac{N}{M}$同时趋向无穷。

而对于加窗的周期图法(时间序列直接加窗)：

$$\begin{aligned} E\{\mathbf{S}_N^{(P)}[k]\} &= \frac{1}{Nf_s} \sum_{p=0}^{N-1}\sum_{q=0}^{N-1} w_p w_q ~~ E\{\mathbf{x}_p \mathbf{x}_q\} ~~ e^{-i \frac{2\pi k}{N} (q-p)}\\ &= \frac{1}{Nf_s} \sum_{p=0}^{N-1}\sum_{q=0}^{N-1} w_p w_q ~~ r_\mathbf{xx}(q-p) ~~ e^{-i \frac{2\pi k}{N} (q-p)}\\ & = \frac{1}{f_s} \sum_{m=-(N-1)}^{N-1} ~~ \frac{1}{N}\sum_{n=0}^{N-|m|-1} w_n w_{n+|m|} ~~ r_\mathbf{xx}(m) e^{-i \frac{2\pi k}{N} m}\\ & = \mathcal{F}\left\{ \frac{w_n * w_n}{N} ~ r_\mathbf{xx}(m)\right\} = |W_N(f)|^2 * S(f) \end{aligned}$$

对应于自相关法，相当于对无偏的自相关估计加以下延迟窗：

$$w'_N = \frac{1}{N} w_N\star w_N = \frac{1}{N} w_N*w_N$$

最简单的，时间序列的矩形窗对应于自相关的三角窗。

可以看到虽然在一定条件下，自相关法与周期图法等价，但两者还是有区别的，尤其是考虑到对自相关加窗是不同于时序信号直接加窗的，前者限制的是计算自相关时的提前或滞后量，而非时序信号长度，也被称为延迟窗(lag window)。自相关加窗等价于对功率谱进行滤波(卷积操作)，可实现功率谱的平滑(降方差)，同时缓解谱泄露引入的偏置，但相应牺牲了频率分辨率。这其中相较窗口形状，更重要的是窗口长度，$\small M=N/K$的效果与$K$折的Welch周期图效果相当。

对周期图方差的理解
随机信号傅里叶变换同样随机(幅值和相位均随机)，因此周期图法的谱估计也是随机变量。具体的，$X_k = \sum x_n e^{-i\frac{2\pi k}{N} n} = \sum x_n \cos\frac{2\pi k n}{N} - i\sum x_n \sin\frac{2\pi k n}{N}$，对于高斯白噪声，$x_n$服从高斯分布，作为$x_n$的线性组合，$X_k$实部和虚部也都服从高斯分布，且方差相同。同时考虑到基函数的正交性，频谱实部虚部(以及不同频率成分)独立，在零均值情况下，经过适当归一化$|X_k|^2$将服从自由度为2的卡方分布，均值2、方差4。
对于零均值高斯白噪声，假设信号功率(方差)为$\sigma^2$，采样频率为Nyquist速率，则：

$$\left|\frac{1}{\sqrt{N}}\sum \frac{x_n}{\sigma}\right|^2 \sim \chi^2_1, ~~ \left|\sqrt{\frac{2}{N}}\sum \frac{x_n \cos\frac{2\pi k n}{N}}{\sigma}\right|^2 \sim \chi^2_1, ~~ \frac{2}{N\sigma^2}|X_k|^2 \sim \chi^2_2$$

由此，离散谱估计$\left|\frac{X_k}{N}\right|^2 \sim \frac{\sigma^2}{2N}\chi^2_2$，均值对应离散谱$\frac{\sigma^2}{N}$，方差为$\left(\frac{\sigma^2}{N}\right)^2$；而功率谱密度估计$\frac{1}{Nf_s}|X_k|^2 \sim \frac{\sigma^2}{2f_s}\chi^2_2$，均值对应谱密度$\frac{\sigma^2}{f_s}$，方差为$\left(\frac{\sigma^2}{f_s}\right)^2$。从功率(能量)角度看，信号能量被分配到了各频段，总功率守恒(Parseval定理)；而从方差(随机性)角度理解，随机性也被分配到各频段，经过取平方，最终功率谱估计的标准差与功率谱本身相当。从$x_n$到$X_k$，时域噪声的随机性被分散到了多个频段，但各频段独立，无法进一步抵消。

对于一般的高斯噪声，可理解为由白噪声经过成形滤波得到，$|X_k|^2=|X'_k|^2S(f)$，考虑到不同频率成分不相关，最终周期图估计各频率分别$\sim \frac{1}{2}S(f)\chi^2_2$，均值为$S(f)$，方差为$S^2(f)$。对于更一般的非高斯噪声结论类似，即频谱的周期图估计是渐近无偏，但不是一致的，方差为频谱自身的平方。这一结论不依赖于样本数(采样数)$N$，因此增加采样时长不能改善功率谱估计的方差。降低频谱估计的方差，需要多次测量取平均，这就是平均周期图法所做的改进，将数据分段计算功率谱，最后求平均。这样做会降低频谱的频率分辨率，但通过求平均，减少了噪声的干扰，$K$段平均后标准差降为初始的$\frac{1}{\sqrt{K}}$。

注意，除白噪声外，周期图估计是渐进无偏，也即有偏的，利用与自相关法的等价性：

$$E\{ \mathbf{S}_N^{(P)}[k] \} = S(f) * \frac{1}{f_s} F_N\left(\frac{2\pi f}{f_s}\right)$$

频谱的动态范围越大，偏置越大。加窗可以减少频谱泄露，降低偏置，但会相应增加谱估计的方差(压低边缘信号，引入了额外波动)，分段求平均则可降低方差。

随机过程运算

分析随机过程功率谱时通常先减去均值，只考虑零均值过程。对于均值非零的广义平稳过程，可理解为零均值过程加上常数，后者会在自相关中贡献常数项，并在功率谱中对应位于零点的$\delta$函数(直流分量)。以下讨论中默认$\mathbf{x}(t)$为零均值广义平稳过程。

• 随机信号相加：$\mathbf{y}(t) = \mathbf{x}_1(t) + \mathbf{x}_2(t)$

  $$r_\mathbf{yy}(\tau) = r_\mathbf{x_1x_1}(\tau) + r_\mathbf{x_2x_2}(\tau) + r_\mathbf{x_1x_2}(\tau) + r_\mathbf{x_2x_1}(\tau)$$

  若两个随机过程$\mathbf{x}_1(t), \mathbf{x}_2(t)$ 不相关，则有$r_\mathbf{yy}(\tau) = r_\mathbf{x_1x_1}(\tau) + r_\mathbf{x_2x_2}(\tau)$，即不相关的零均值广义平稳过程相加的自相关函数为各自自相关函数之和。对应功率谱有$S_\mathbf{yy}(f) = S_\mathbf{x_1x_1}(f) + S_\mathbf{x_2x_2}(f)$，即不相关的零均值广义平稳过程相加的功率谱为各自功率谱之和。

• 随机信号与确定信号相加：$\mathbf{y}(t) = \mathbf{x}(t) + s(t)$

  $$r_\mathbf{yy}(t, \tau) = r_\mathbf{xx}(\tau) + \overline{s(t)}\mu_\mathbf{x} + s(t+\tau)\overline{\mu_\mathbf{x}} + \overline{s(t)}s(t+\tau)$$

  考虑到$\mathbf{x}(t)$为零均值过程有$r_\mathbf{yy}(t, \tau) = r_\mathbf{xx}(\tau) + \overline{s(t)}s(t+\tau)$。一般情况，$\mathbf{y}(t)$的均值和自相关函数都依赖$t$，为非平稳过程，也就不存在功率谱。特例是当$s(t) = e^{i\omega_s t}, ~ \overline{s(t)}s(t+\tau)=e^{i\omega_s \tau}$，此时互相关并不依赖时间（均值依然依赖时间），功率谱相比$\mathbf{x}(t)$处多在频率$\frac{1}{2\pi}\omega_s$处的$\delta$函数。尤其是当$s(t)$为常数，此时$\mathbf{y}(t)$仍为广义平稳过程，功率谱相比$\mathbf{x}(t)$多了在零点处的$\delta$函数。

• 随机信号与确定信号相乘：$\mathbf{y}(t) = \mathbf{x}(t) s(t)$

  $$r_\mathbf{yy}(t, \tau) = \overline{s(t)}s(t+\tau)r_\mathbf{xx}(\tau)$$

  一般情况，$\mathbf{y}(t)$的均值和自相关函数都依赖$t$，为非平稳过程，也就不存在功率谱。特例是当$s(t) = e^{i\omega_s t}, ~ \overline{s(t)}s(t+\tau)=e^{i\omega_s \tau}$，此时互相关并不依赖时间，$\mathbf{y}(t)$仍为广义平稳过程，且此时有$S_\mathbf{yy}(f) = S_\mathbf{xx}(f-\frac{1}{2\pi}\omega_s)$，即功率谱对称中心由零点平移至$\frac{1}{2\pi}\omega_s$。
  此外，对于实信号$s(t) = \cos\omega_s t$，其自相关函数依赖时间，但具有周期性，如果对周期平均后计算功率谱有$S_\mathbf{yy}(f) = \frac{1}{4}[S_\mathbf{xx}(f+\frac{1}{2\pi}\omega_s) + S_\mathbf{xx}(f-\frac{1}{2\pi}\omega_s)]$。

• 随机信号滤波：$\mathbf{y}(t) = \mathbf{x}(t) * h(t)$

  $$E\{\mathbf{y}(t)\} = E\{\mathbf{x}(t)\}H(0)$$

  其中$H(0)$为$h(t)$傅里叶变换在零点的取值，对零均值过程$\mathbf{x}(t)$，$\mathbf{y}(t)$均值也为零。从信号处理系统角度理解，卷积形式的系统是线性时不变的，$h(t)$为系统脉冲响应，$H(f)$为对应的频响函数，而$H(0)$被称为系统的直流增益(DC Gain)。

  $$r_\mathbf{yx}(\tau) = r_\mathbf{xx}(\tau) * h(\tau), ~~~ r_\mathbf{xy}(\tau) = r_\mathbf{yx}(-\tau) = r_\mathbf{xx}(\tau) * h(-\tau)$$

  $$r_\mathbf{yy}(\tau) = r_\mathbf{xy}(\tau) * h(\tau) = r_\mathbf{xx}(\tau) * h(-\tau) * h(\tau)$$

  $$S_\mathbf{yy}(f) = S_\mathbf{xx}(f) |H(f)|^2$$

噪声与信噪比

彩色噪声

类似于包含各波长的可见光为白光，各频率功率均等的随机信号被称为白噪声，对应功率谱密度为常数。所有频谱不为常数的随机噪声都被称为有色噪声：类比可见光，当低频成分占比多时，颜色偏红，功率谱$∝f^{-1}$被称粉红噪声，$∝f^{-2}$则被称为红噪声；当高频成分占比多时，颜色偏蓝，功率谱$∝f$被称为蓝噪声，$∝f^2$则被称为紫噪声。

不过很多时候，颜色的区分并不严格，红噪声可能指代任何低频功率更高或功率谱呈负指数分布的噪声，相反高频成分偏多的噪声被统称为蓝噪声。负指数谱(红)，低频成分占比多，系统自相关性持续较长，具有长时记忆；正指数谱(蓝)，高频成分占比多，系统具有反持久性，相邻增量间反相关，前者在信号处理中很常见。
相邻信号正相关、相邻增量反相关

• 白噪声：$S(f)\propto 1$
  热噪声(thermal noise)和散粒噪声(shot noise)是常见的高斯白噪声：

  • 热噪声：电子设备中无源器件，由于大量电子热运动引起的噪声
  • 散粒噪声：电子设备中有源器件，由于电子发射不均匀性(涨落)所引起的噪声

  白噪声功率谱密度为常数，通常记为$N_0$，对于实信号默认指的单边PSD，对应的双边PSD为$N_0/2$；复信号没有单边PSD，$N_0$就是双边PSD。傅里叶逆变换可得到自相关函数$r_\mathbf{xx}(\tau) = \frac{N_0}{2}\delta(\tau)$，即任意不同时刻信号相关$E\{\mathbf{x}(t_1)\mathbf{x}(t_2)\}$为零，相同时刻信号相关$E\{\mathbf{x}^2(t)\}$发散。前者代表白噪声随机过程前后不存在关联，后者则对应零均值信号的方差以及功率$\sigma^2 = E\{\mathbf{x}^2(t)\} = r_\mathbf{xx}(0) = \int S(f)df = P$，从而理想白噪声信号的功率/方差无限大。

  现实中白噪声一般有较广但有限的带宽，通常会先对信号进行低通或带通滤波，之后再以超过Nyquist速率的采样率进行采样。此时：

  $$\sigma^2 = E\{\mathbf{x}^2(t)\} = r_\mathbf{xx}(0) = \int \frac{N_0}{2}|H(f)|^2df = N_0 B$$

  $H(f)$为滤波器频率响应，$B$为带宽。理想低通滤波$|H(f)|^2=2B{\rm rect}(\frac{f}{2B})$，对应自相关函数由$\delta$函数展宽为${\rm sinc}$函数$r_\mathbf{xx}(\tau) = N_0B{\rm sinc}(2B\tau)$。若以Nyquist频率2B进行采样，离散的自相关函数表现为$r_\mathbf{xx}[k] =N_0B \delta[k]$，这里$\delta[k]$为克氏符，而非狄拉克$\delta$函数，在$\tau=0$处取1，其余位置为0。

  注意区分功率$\sigma^2$与谱密度$N_0$，两者容易混淆。一些地方会出现$S(f)=\sigma^2$，这其实只针对归一化频率$f/f_s$，此时对应频率范围为$[-\frac{1}{2}, \frac{1}{2})$，有$N_0=\sigma^2$。

• 粉噪声：$S(f)\propto 1/f$ 1/f噪声、闪烁噪声
  粉红噪声也被为1/f噪声，功率谱密度$∝1/f$，功率在对数频率间隔上均匀分布，即等比频带功率相同。粉红噪声的常见实例有电子元件的闪烁噪声(flicker noise)，以及人的心电图、脑电图等生物信号。人的听觉系统对高频更敏感，因此音阶(八度)划分也是对数均匀的。白噪声在听觉上会表现得刺耳(高频过剩)，对数均匀的粉噪声反而更均衡，因此粉红噪声会被用作声学的参考信号。而要各频率听感完全均衡(灰噪声)，则需针对个人的听觉感知专门定制，主要用于心理学。

• 红噪声：$S(f)\propto 1/f^2$ 布朗噪声、褐噪声
  红噪声也被称为布朗噪声或随机游走噪声，功率谱密度$∝1/f^2$。“褐噪声”的说法虽然很常见，但感觉是误用，“Brown”对应其实是布朗运动。布朗运动是随机运动的累积，粒子每次位移量对应白噪声，而粒子与初始位置的位移量则对应布朗噪声(红噪声)，红噪声对应于白噪声的时间积分。红噪声低频端能量更高，听起来类似大雨、瀑布、海浪等所产生的低沉声响。

噪声模拟

对于白噪声，最常用的形式是(均值为零的)独立同分布(i.d.d.)过程，具体分布并没有要求。当共同分布为零均值正态分布时，又被称为高斯白噪声。注意，单独的高斯噪声，仅要求随机信号服从高斯分布，但并不要相互独立，也就不一定是白噪声。

模拟高斯白噪声，可直接按$x_n \sim \mathcal{N}(0, \sigma^2)$采样得到时间序列，其中方差对应信号功率。需注意的是，不同于现实噪声，通过这种方式模拟的白噪声，功率有限，频率范围却是无限制的，生成的采样信号带宽完全由采样频率决定。$\sigma^2$的总功率分配到$[-\frac{f_s}{2}, \frac{f_s}{2})$的频率区间，对应功率谱密度$\sigma^2/f_s$；分配到N个频率区间，对应离散功率谱$\sigma^2/N$。这种情况下，噪声的自相关函数可理解为$r_\mathbf{xx}[k] = \sigma^2\delta[k]$，这里$\delta[k]$为克氏符，而非狄拉克$\delta$函数。$\sigma^2$固定意味模拟噪声的功率谱或谱密度依赖具体的采样设置，谱密度随采样频率增加而降低，而离散谱随采样点数增加降低，保持恒定的是$E\left\{\frac{|X_k|^2}{N}\right\} = \sigma^2$。

实际信号通常是功率谱$\left|\frac{X_k}{N}\right|^2$(离散频率信号)或谱密度$\frac{|X_k|^2}{N f_s}$(连续谱信号)保持恒定。噪声通常呈现连续谱，现实白噪声，带宽有限，功率及谱密度恒定：如果$f_s$低于Nyquist采样率，将出现混叠，部分频率谱密度会被抬升；当$f_s$高于Nyquist采样率，则谱密度在低频部分保持不变，高频出现截断，继续增加采样率谱密度并不变。

对于一般的噪声功率谱密度(PSD)$S_n(f)$，如何生成对应的(高斯)噪声时间序列？

根据功率谱的周期图估计$S(f) = \frac{1}{T}|X(f)|^2 = \frac{1}{Nf_s}|X_k|^2$，可以得到信号DFT频谱幅值为$|X_k| = \sqrt{N f_s S(f)}$。对于相位，如果不同频率成分不相关，可取为$[0, 2\pi)$均匀分布，从而$X_k = \sqrt{N f_s S(f)} e^{i\phi_k}$，最后变换回时域即可得到时间序列。事实上可以证明，对于平稳信号，不同频率成分确实是不相关(正交)的：

$$\begin{aligned} E\left\{\overline{\mathbf{X}(f_1)}\mathbf{X}(f)\right\} &= E\left\{ \int \mathbf{x}(t_1)e^{i 2\pi f_1 t_1}dt_1 \int \mathbf{x}(t)e^{-i 2\pi f t}dt \right\}\\ & = \int E\left\{ \mathbf{x}(t_1) \mathbf{x}(t_1+\tau)\right\} e^{i 2\pi f_1 t_1}e^{-i 2\pi f (t_1+\tau)} dt_1d\tau \\ & = \int r_\mathbf{xx}(\tau) e^{-i 2\pi f \tau} d\tau \int e^{i 2\pi (f_1-f) t_1} dt_1 \\ & = S(f)\delta(f_1-f) \end{aligned}$$

这里利用了自相关函数的稳定性(不依赖$t_1$)，对二阶平稳随机过程成立。最后，在实现时需注意零频率和Nyquist频率对应的复谱$X_k$必须为实数：

$$X_k=\begin{cases} \sqrt{f_s N \frac{1}{2}S_{\tiny +}(f_k)} e^{i\phi_k} &\text{if} ~~ 0<k<\frac{N}{2}\\ \sqrt{f_s N S_{\tiny +}(f_k)} &\text{if} ~~ k=0, ~ \frac{N}{2}\end{cases}$$

注意这里只考虑正频率，$S_{\tiny +}(f_k)$为单边谱，相应的需要用单边DFT。对于零均值的随机过程，$S_{\tiny +}(0) = 0$，从而$X_0=0$。简单取$S(f_k)= N_0$可得到白噪声，不同于前面时域方法，这里固定谱密度，平均功率或信号方差将随采样频率变化$\sigma^2=\frac{N_0}{2}f_s$。

这里有个问题：随机的只有相位，幅值是确定的，而根据前面对周期图法的分析，幅值是服从$\chi^2_2$的随机变量。Timmer & Koenig 1995据此认为更合理的噪声生成方式是：

$$X_k=\begin{cases} [\mathcal{N}(0, 1) + i\mathcal{N}(0, 1)]\frac{1}{2} \sqrt{N f_s S_{\tiny +}(f_k)} &\text{if} ~~ 0<k<\frac{N}{2}\\ \mathcal{N}(0, 1) \sqrt{N f_s S_{\tiny +}(f_k)} &\text{if} ~~ k=0, ~ \frac{N}{2}\end{cases}$$

这里复频谱的实部与虚部作为完全独立的随机变量，与前面频谱相位随机分布相对应，所不同的是幅值也具有了随机性。注意$S_{\tiny +}(f_k)$为单边谱，且零频率和Nyquist频率对应的复谱$X_k$为实数，服从正态分布。astroML中彩色噪声模拟就用了该算法。

还有一种思路是先在时域生成高斯白噪声，DFT得到对应复谱，再使用成形滤波$\sqrt{S(f)}$变换得到复频谱，这个过程只改变了幅值，不改变相位。

$$x^{(w)}_n \sim \mathcal{N}(0, 1), ~~~ X_k = X^{(w)}_k\sqrt{f_s S(f)}$$

其中红噪声和紫噪声可通过对白噪声信号简单积分(自回归AR)和差分(移动平均MA)得到。

最后，Matlab中使用了更为复杂的实现方式：负指数谱用的是自回归AR模型，除了粉红和红噪声使用双二次IIR滤波器(sosfilt)；正指数谱则是移动平均MA模型，除了紫噪声使用一阶滤波器，不清楚这样选择的优势。

import numpy as np
from scipy import signal
from matplotlib import pyplot as plt

def generate_noise(N, fs, color, noise_generater, seed=None):
    # power low psd functions
    noise_power_index = {'white': 0, 'pink': -1, 'red': -2}
    def power_law_spectra(alpha):
        return lambda f: np.power(f, alpha, where=(f!=0))

    slope = noise_power_index[color]
    psd_func = power_law_spectra(slope)

    L = N//2 + 1
    freqs = np.arange(L)*fs/N
    psd_scaled = psd_func(freqs) * fs
    # psd变为psd*fs，以对应归一化频率

    noises = noise_generater(N, psd_scaled, seed)
    return noises, psd_scaled

def psd_compare(noise_generater, random_seed=42):
    T, fs = 10, 4096
    N = int(T*fs)
    for color in ['white', 'pink', 'red']:
        noises, psd_scaled = generate_noise(N, fs, color,
                              noise_generater, random_seed)
        freqs, psd = signal.periodogram(noises, fs=fs)
        if color == 'white':
            color = 'grey'
        plt.loglog(freqs, psd, color=color)
        plt.loglog(freqs, psd_scaled/fs)
        plt.ylim(1e-12, 1e3)
    plt.show()

def show_noise(noise_generater, random_seed=42):
    T, fs = 10, 4096
    N = int(T*fs)
    times = np.arange(N)/fs
    for color in ['white', 'pink', 'red']:
        noises, psd_scaled = generate_noise(N, fs, color,
                              noise_generater, random_seed)
        sigma = np.sqrt(np.sum(psd_scaled)/N)
        if color == 'white':
            color = 'grey'
        plt.plot(times, noises/sigma, color=color)
    plt.show()

def noise_from_psd1(N, psd, seed):
    L = N//2 + 1
    A_k = np.sqrt(psd/2 * N)
    rng = np.random.default_rng(seed)
    phases = rng.uniform(0., 2*np.pi, size=L)
    X_k = A_k*np.exp(1j*phases)
    X_k[0] = A_k[0]*np.sqrt(2)
    if N % 2 == 0:
        X_k[-1] = A_k[-1]*np.sqrt(2)

    noises = np.fft.irfft(X_k)
    return noises

def noise_from_psd2(N, psd, seed):
    L = N//2 + 1
    rng = np.random.default_rng(seed)
    X1 = rng.normal(0., 1., size=L)
    X2 = rng.normal(0., 1., size=L)
    X_k = (X1 + 1j*X2)/2 * np.sqrt(psd * N)
    X_k[0] = 2*X_k[0].real
    if N % 2 ==0:
        X_k[-1] = 2*X_k[-1].real

    noises = np.fft.irfft(X_k)
    return noises

def noise_from_psd3(N, psd, seed):
    rng = np.random.default_rng(seed)
    X_white = np.fft.rfft(rng.normal(0, 1, N))
    X_k = X_white * np.sqrt(psd)

    noises = np.fft.irfft(X_k)
    return noises

psd_compare(noise_from_psd1)
psd_compare(noise_from_psd2)
psd_compare(noise_from_psd3)
show_noise(noise_from_psd3)

def psd_mean(noise_generater, random_seed=None):
    T, fs = 10, 4096
    N = int(T*fs)
    color = 'white'# ['white', 'pink', 'red']
    for _ in range(10):
        noises, psd_scaled = generate_noise(N, fs, color,
                              noise_generater, random_seed)
        freqs, psd = signal.periodogram(noises, fs=fs)
        if color == 'white':
            color = 'grey'
        plt.loglog(freqs, psd, color=color)
        plt.loglog(freqs, psd_scaled/fs)
        plt.ylim(1e-12, 1e3)
    plt.show()

SNR is the ratio of detected signal to uncertainty of the signal measurement. Higher is better.

系统灵敏度是对于给定的SNR和观测时长，系统所能分辨的流量水平下限。
泊松分布期望和方差都为$\lambda$，信噪比期望比标准差，

SNR提升

常见噪声

• 信号自身(散粒噪声)：光子到达时间随机性造成的流量波动
  信号光子到达时间本身不确定(泊松分布)，会造成观测流量的内禀波动。而且除了目标天体外，观测还会受到天体以及地面环境光的影响，这些额外的信号可通过一定技术扣除，但信号的内禀波动(散粒噪声)却无法消除，最终提升噪声水平。根据泊松统计，每秒到达的光子数波动方差与期望相等，随观测时长增加方差和期望随之增长。信噪比为期望与标准差之比，因此正比于积分时长开根号。
• 读出噪声(量化噪声)：信号读出过程(模拟变数字)引入的噪声
  读出电路整体噪声
  There are usually a number of sources in the circuitry of a sensor and it’s readout logic that can add noise to the image signal, and generally manufacturers lump them all together as an RMS (root mean square) called “read noise”.
• 暗电流噪声(热噪声)：

提升SNR

• 堆栈(stacking)：增加积分时长
• 滤光片(filter)：窄带滤波

平稳信号提升信噪比
增加采样时间 不行
信号分段平均 不行
增加采样时间 + 求平均 行
分辨率低、信噪比好、但幅值估计不准??

https://jonrista.com/the-astrophotographers-guide/astrophotography-basics/snr/

在单次观测中读出噪声是固定的，不随积分时间变化，但却会随着堆栈次数增加，因此在不过曝的前提下优先增加积分时间，之后再进行堆栈。
However using longer exposures is also another way to increase integration time. So long as you are not exposing too long, and thus needlessly wasting dynamic range, it is generally better to expose for longer first, before increasing how many subs you are stacking. Once you have reached a reasonable limit on exposure time, then the best way to improve SNR is by stacking

匹配滤波技术

假设噪声是与信号不相关的加性噪声有：

$$\mathbf{x}(t) = s(t-t_0) + \mathbf{n}(t), ~~~ \mathbf{y}(t) = h(t)*\mathbf{x}(t)$$

匹配滤波

这里先从“相关”视角建立对匹配滤波的直观理解。在数据噪声为白噪声时，匹配滤波就是信号模板$s(t)$与数据$\mathbf{x}(t)$的直接相关操作：

$$\mathbf{y}(t) = (s\star \mathbf{x})(t) = \int s(\tau-t) \mathbf{x}(\tau) d\tau, ~~~~ Y(f) = \overline{X_s(f)}X(f)$$

频域形式可由傅里叶变换的相关定理或卷积定理得到：$s(t)$为实函数，相关等价于反转卷积，同时对于实函数$s(-t)$，傅里叶变换为$\overline{X_s(f)}$。而在时域上有$\mathbf{y}(t) = r_{ss}(t-t_0) + r_{s\mathbf{n}}(t)$。由于信号与噪声不相关$E\{r_{s\mathbf{n}}(t)\}=0, E\{\mathbf{y}(t)\}= r_{ss}(t-t_0)$，反映了时刻$t$模板与信号的匹配度，在$t=t_0$处取最大值。

对于非白噪声情况，匹配滤波是将信号模板与数据分别用噪声功率谱$S_n(f)$白化后，再进行相关操作。在频域上有：

$$Y(f) = \frac{\overline{X_s(f)}}{\sqrt{S_n}}\frac{X(f)}{\sqrt{S_n(f)}} = \frac{\overline{X_s(f)}X(f)}{S_n(f)}$$

相比白噪声时的$\overline{X_s(f)}X(f)$，核心区别在于用噪声功率谱倒数进行了加权，增加了低噪频段的相对权重，最终可提升整体的信噪比。变换到时域为：

$$\mathbf{y}(t) = \mathcal{F}^{-1}\left\{\frac{X_s(f)}{\sqrt{S_n(f)}}\right\} \star \mathcal{F}^{-1}\left\{\frac{X(f)}{\sqrt{S_n(f)}}\right\}=\mathcal{F}^{-1}\left\{\frac{X_s(f)}{S_n(f)}\right\} \star \mathbf{x}(t)$$

最终$\mathbf{y}(t) = r_{s's'}(t-t_0) + r_{s'\mathbf{n}}(t), s'(t) = \mathcal{F}^{-1}\left\{\frac{X_s(f)}{S_n(f)}\right\}$。类似白噪声情况，$\mathbf{y}(t)$反映了时刻$t$模板与信号的匹配度，取最大值时对应信号在数据中出现的时刻$t_0$。注意，实际计算中通常会使用单边谱，此时$\mathbf{y}(t)$不再是实信号，需要对比$|\mathbf{y}(t)|$。

实际中$s(t)$通常预先并不清楚，要从大量备选中筛选匹配度最高的模板。而相关结果依赖模板自身幅值，如$s(t)$与$k~s(t)$，波形相同，结果相差常数倍$k$。因此对比前需要对模板总能量进行归一化$X_{\frak t} \rightarrow X_{\frak t} /\sqrt{E}, E = \int \left| X_{\frak t}(f) \right|^2 df$。事实上，更好的选择是用白化后模板能量进行归一化$E ={\displaystyle \int} \left| \frac{\overline{X_{\frak t}(f)}}{\sqrt{S_n(f)}} \right|^2 df$，此时：

$$\hat{\mathbf{y}}(t) = \mathcal{F}^{-1}\left\{\frac{\overline{X_{\frak t}(f)}X(f)}{S_n(f)}\right\} / \sqrt{\int \frac{ \left|X_{\frak t} (f) \right|^2}{S_n(f)} df}$$

归一化后，$\hat{\mathbf{y}}(t)$不仅可确定模板匹配度最高时刻，还可用于对比不同模板，事实上$\hat{\mathbf{y}}(t)$就对应于输出信号的信噪比。此时输出噪声$\hat{\mathbf{y}}_\mathbf{n}(t)$功率谱为$\left|\frac{\overline{X_{\frak t}(f)}}{S_n(f)}\right|^2 S_n(f) / \int \frac{ \left|X_{\frak t} (f) \right|^2}{S_n(f)} df$，平均功率$E\{\hat{\mathbf{y}}^2_\mathbf{n}(t)\}=1$，从而任意时刻信噪比为

$$\mathrm{SNR}(t) = \frac{P_{y_s}(t)}{P_\mathbf{y_n}(t)} = \frac{E\{\hat{\mathbf{y}}(t)\}^2}{E\{\hat{\mathbf{y}}^2_\mathbf{n}(t)\}} = E\{\hat{\mathbf{y}}(t)\}^2 = \hat{y}^2_s(t)$$

这就是用白化后模板能量进行归一化的好处。最后，可以证明，当模板与信号相匹配时信噪比最大：

$$\mathrm{SNR}(t) = \hat{y}^2_s(t) = \left|\frac{ \int \frac{\overline{X_{\frak t}(f)}X_s(f)e^{-i2\pi f t_0}}{S_n(f)}e^{i2\pi f t} df }{ \sqrt{\int \frac{ \left|X_{\frak t} (f) \right|^2}{S_n(f)} df} }\right|^2 \le \int \frac{ \left|X_s (f) \right|^2}{S_n(f)} df$$

上面利用了柯西-施瓦兹不等式$\left|\int f(x) g(x) dx\right|^2 \le \int |f(x)|^2 dx \int |g(x)|^2 dx$，其中等号当且仅当$f(x)=k\overline{g(x)}$时成立。等号成立时有$X_{\frak t}(f)=k X_s(f), t=t_0$，即在模板为$ks(t)$(与信号相匹配)，时间为$t_0$(信号出现时刻)时信噪比最大。

最后，从通常的“滤波”角度理解，结论是一致的：

$$\mathbf{y}(t) = y_s(t) + \mathbf{y_n}(t) = s(t-t_0)*h(t) + \mathbf{n}(t)*h(t)$$

$$y_s(t) = \mathcal{F}^{-1}\left\{Y_s(f)\right\}, ~~ Y_s(f) = X_s(f)e^{-i2\pi ft_0}H(f)$$

$$\mathrm{SNR}(t) = \frac{y^2_s(t)}{E\left\{ \mathbf{y}^2_n(t)\right\} } = \frac{\displaystyle\left|\int X_s(f)H(f) e^{i2\pi f (t-t_0)} df\right|^2}{\displaystyle\int S_n(f)|H(f)|^2 df} \le \int \frac{|X_s(f)|^2}{S_n(f)} df$$

上式同样利用了柯西-施瓦兹不等式，信噪比在$t_0$时刻取得最大值，同时滤波器频率响应$H(f) = k\frac{\overline{X_s(f)}}{S_n(f)}$(用噪声功率谱对反转信号频谱加权)。

信号白化的计算

$$\frac{X(f)}{\sqrt{S_n(f)}}$$

白化后功率谱密度为1，

为什么看到别人的实现中没有$N$？只有$f_s$，计算$S_n$时$N = f_s$，还是不对！
白化后功率谱为1？？

参数估计

匹配滤波只能实现点估计，且受模板网格精细度限制，要获得参数不确定性，需要基于概率分布，利用Fisher信息矩阵(FIM)、MCMC采样等进行区间估计。

Maggiore 2008 GW 7.4.2
The PyCBC search for gravitational waves from CBCs

常见随机过程

Random Processes
Some Important Random Processes
Stats 325 https://www.stat.auckland.ac.nz/~fewster/325/notes.php

https://www.datasciencecentral.com/profiles/blogs/fee-book-applied-stochastic-processes 需要订阅 Data Science Central才能获取

https://en.wikipedia.org/wiki/Stochastic_process
https://www.math.ucdavis.edu/~hunter/m280_09/ch5.pdf

https://dlsun.github.io/probability/random-process.html

高斯过程

(白噪声) 自相关为$\delta$函数，频谱为恒定
An intuitive guide to Gaussian processes

泊松过程

The Poisson Distribution and Poisson Process Explained

马尔可夫

列维过程
离散马尔科夫
连续马尔科夫
PageRank 马尔科夫稳态分布

随机游走

维纳过程
随机游走：布朗运动、高斯随机游走
布朗运动，布朗运动是高斯过程的积分(红噪声)
Relation to Wiener process

时间序列技术

时间序列分析基础-定义、均值、方差、自协方差及相关性

Applied Time Series Analysis in Python
Time Series Modeling AR, StateSpace

随机游走RW

自回归移动平均ARMA

移动平均MA
自回归AR
ARMA/ARIMA

Stationary Random Processes
Random Process - TaigaComplex
Does the autocorrelation function completely describe a stochastic process?
Generating coloured noise to simulate physical processes

Astrophotography Basics: SNR