信号分析：基础概念

https://en.wikipedia.org/wiki/Signal_processing
傅里叶变换、相关、卷积
频谱、功率谱、周期图

光的色散对应信号的傅里叶分析，光谱对应信号频谱

衍射条纹光强对应的是孔径函数傅里叶变换的幅值
光栅衍射则对应周期性函数的傅里叶变换

Signal Recovery with Differentiable Scalograms and Spectrograms
用相位来训练模型??

Measure Power of Deterministic Periodic Signals

Practical Statistics for Astronomers 第8章
Statistics, Data Mining, and Machine Learning in Astronomy 第10章
Analysis of Gravitational Wave Data
https://pysdr.org/content/frequency_domain.html

傅里叶变换及其应用学习笔记 - TaigaComplex
离散时间信号处理学习笔记 - TaigaComplex
随机过程学习笔记 - TaigaComplex
卡尔曼滤波器详解——从零开始
Spectrum and spectral density estimation by DFT
Signals, Sampling, & Filtering - Scientific Computing

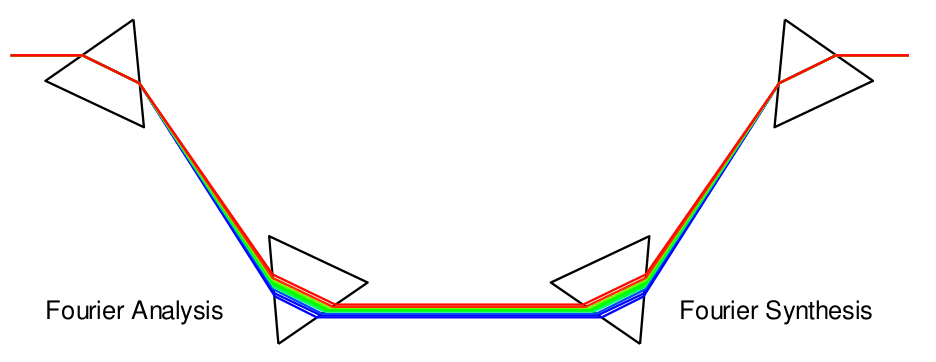
傅里叶分析与合成

傅里叶变换 FT

傅里叶分析最初是研究周期性现象，对于周期函数，利用傅里叶级数(Fourier Series)，可将其展开为离散频率(谐频)三角函数的无限求和，展开系数由函数的单个周期决定。

$$x(t) = \sum_{k=-\infty}^{\infty} \alpha_k e^{i \frac{2\pi k}{T} t}, ~~~ \alpha_k = \frac{1}{T}\int_{-T/2}^{T/2} x(t) e^{-i \frac{2\pi k}{T} t} dt$$

这里三角函数使用了复数形式(欧拉公式)，为得到实信号，系数$a_k$也需要是复数，其模长对应频率成分的振幅，幅角则对应频率成分的相位偏置。

对于非周期函数，可将其视为周期$\infty$的周期函数，对上述傅里叶级数进行推广。不过直接根据上式，随$T\rightarrow \infty$，将有$\alpha_k \rightarrow 0$（假设$x(t)\in L^1(\R)$），因此需要稍作变换：

$$\beta_k = \int_{-T/2}^{T/2} x(t) e^{-i \frac{2\pi k}{T} t} dt, ~~~ x(t) = \frac{1}{T} \sum_{-\infty}^{\infty} \beta_k e^{i \frac{2\pi k}{T} t}$$

当$T\rightarrow \infty, \frac{1}{T}\rightarrow 0$，谐频$\frac{k}{T}$ 变为连续变量，积分变为求和。令$f=\frac{k}{T}, df=\frac{1}{T}$：

$$\boxed{X(f) = \int x(t) e^{-i 2\pi f t} dt, ~~~ x(t) = \int X(f) e^{i 2\pi f t} df}$$

这就是傅里叶变换(Fourier Transform)。
将频率$f$替换为角频率$\omega=2\pi f$有：

$$X(\omega) = \int x(t) e^{-i\omega t} dt, ~~~ x(t) = \frac{1}{2\pi} \int X(\omega) e^{i \omega t} d\omega$$

注意这里正逆变换的对称性被破坏，因此又有另一种定义形式：

$$X(\omega) = \frac{1}{\sqrt{2\pi}} \int x(t) e^{-i\omega t} dt, ~~~ x(t) = \frac{1}{\sqrt{2\pi}} \int X(\omega) e^{i \omega t} d\omega$$

注：这里符号上未做区分，但显然上面三种定义下的$X$是不同的。

• 分布的傅里叶变换
  上面定义的傅里叶变换只在积分收敛时有意义，对于常数、$\sin, \cos$等积分不收敛的函数并没有意义。简单的我们可以对这些情况进行特殊定义，如引入广义函数$\delta(x)$。更一般的，在数学上则是引入“分布”(一种广义函数而非概率分布，最典型的就是$\delta$函数)的概念对傅里叶变换的定义进行扩展。以最速降函数为测试函数，常数、$\sin, \cos, x^n$等作为缓增分布(tempered distribution)，其傅里叶变换有了定义。这里不做展开，直接使用$\delta$函数的结果。
• 不确定性原理
  在时域对信号进行拉伸对应在频域对其频谱压缩，这是傅里叶变换的缩放性质。这意味信号在时域和频域的弥散度是对偶：持续时间越短的信号，对应的频率范围(频带)通常越宽；相反，越持续的信号频带越窄。这在直觉上也是可理解的，持续时间越短的信号，其具体频率越不确定，而随着观测时间延长，频率的确定性提升。最典型的，无限延伸的常数、正余弦等信号对应无限压缩的$\delta$函数。
  直观看待不确定性原理：不只是量子现象
  在数学上，函数的弥散程度可由其二阶距(方差)描述$\int_{-\infty}^{\infty} t^2|x(t)|^2 dt$，将其归一化$\frac{\int_{-\infty}^{\infty} t^2|x(t)|^2 dt}{\int_{-\infty}^{\infty} |x(t)|^2 dt}$并记为$\Delta_x$，表示$x(t)$(关于零点)的弥散程度，相应的$\Delta_X$表示其傅里叶变换$X(f)$的弥散程度，则在一系列连续和(平方)可积的条件下，有：$\Delta_x\Delta_X \ge \frac{1}{16\pi^2}$，这是傅里叶变换的不确定性原理。在量子理学中，就对应于更著名的海森堡不确定性原理。

上面FT变换为$L^{1}(\R)$函数空间的线性变换，变换前后的函数空间中函数定义域均为$\R$(且绝对可积)，值域则为复数。虽然定义域均为实数，但两者具有相反的单位尺度，如时间$t$对应频率$f=1/T$，长度对应波数$k=1/\lambda$，而$t/2\pi$则对应$\omega = 2\pi f$。值得一提的，量子力学中位置空间的波函数傅里叶变换是动量空间的波函数($p=hk$)。对于定义域$\in\R^n$的可积函数，可类似定义$L^{1}(\R^n)$下的FT变换，相关运算变为矢量形式。

$X(\omega)$为复值函数，$X(\omega) = |X(\omega)|e^{i\phi(\omega)}$，其模长$|X(\omega)|$对应频率成分的振幅(幅度谱)、幅角$\phi(\omega)$对应频率成分的相位偏置(相位谱)。对实信号有$\boxed{X(-\omega) = \overline{X(\omega)}}$，从而负频率信息是不必要的。从频谱角度看，实信号幅度谱为偶函数，相位谱为奇函数；而从变换角度看，$X(\omega)$实部为偶函数，虚部为奇函数，逆变换时正负频率对应值的实部相叠加、虚部相抵消，即对于逆变换有：

$$\displaystyle x(t) = \int_{-\infty}^{\infty} X(f) e^{i 2\pi f t} df = \int_{-\infty}^{\infty} \mathrm{Re} \left( X(f) e^{i 2\pi f t} \right) df$$

以$\mathcal{F}$表示傅里叶变换，$\mathcal{F}^{-1}$表示逆变换，傅里叶变换的常用性质有：

• 零点值

  $$X(0)=\int x(t) dt, ~~~ \int X(f) df = x(0)$$

  零频率成分的谱值 $X(0)$ 通常被称为信号的直流DC偏置或平均值。

• 常见变换：$1, ~ e^{it}, ~ e^{-\pi t^2}, ~ {\rm rect}(t), ~ {\rm tri}(t)$

  $$1 \leftrightarrow \delta(t), ~~~~ e^{it} \leftrightarrow \delta(f-\frac{1}{2\pi}), ~~~~ e^{-\pi t^2} \leftrightarrow e^{-\pi f^2}$$

  $${\rm rect}(f) \leftrightarrow {\rm sinc}(f), ~~~~~~ {\rm tri}(t) \leftrightarrow {\rm sinc}^2(f)$$

  其中值得注意的，高斯函数的FT还是高斯函数，对应于傅里叶变换这个线性算子的本征函数，当然不限于高斯函数，任何$f$，$f+\mathcal{F}f+\mathcal{F}^2f+\mathcal{F}^3f$都满足要求。
• 线性

  $$\mathcal{F}\{f + g\} = \mathcal{F}\{f\} + \mathcal{F}\{g\}, ~~~ \mathcal{F}\{a f\} = a\mathcal{F}\{f\}$$

  前者为可加性，后者为齐次性，两者共同构成叠加原理，是线性系统的核心特征。
• 平移

  • $$\mathcal{F}\{x(t-t_0)\} = e^{-i\omega t_0}X(\omega) = |X(\omega)|e^{i[\theta(\omega)-\omega t_0]}$$

    时域的时移对应频域的相移

  • $$\mathcal{F}\left\{x(t)e^{i\omega_0 t}\right\} = X(\omega-\omega_0)$$

    时域的频移(幅度调制)对应频域的平移
    对实信号$\mathcal{F}\left\{x(t)\cos(\omega_0 t)\right\} = {\displaystyle\frac{1}{2}} [X(\omega-\omega_0) + X(\omega+\omega_0)]$
• 缩放

  $$\mathcal{F}\{x(at)\} = \frac{1}{|a|} X\left(\frac{\omega}{a}\right)$$

  时频域缩放对偶：时域横向压缩，频域横向展宽(同时纵向压低)，时域横向展宽，频域横向压缩(同时纵向提升)。时域与频域的定域性不可兼得(不确定性原理)。
• 反转

  $$\mathcal{F}\{x(-t)\} = \mathcal{F}^{-1}\{x(t)\} = X(-\omega)$$

  函数反转的FT = 函数傅里叶逆变换IFT = 函数FT后反转(时间反转对应频率反转)
  对于实函数$x(t)$，$X(-\omega)=\overline{X(\omega)}$，从而$\mathcal{F}\{x(-t)\} = \overline{X(\omega)}$
• 共轭

  $$\mathcal{F}\left\{\overline{x(t)}\right\} = \overline{\mathcal{F}\left\{x(-t)\right\}} = \overline{X(-\omega)}$$

• 周期性/对偶性

  $$\mathcal{F}\mathcal{F}\{x(t)\} = \mathcal{F}\mathcal{F}^{-1}\{x(-t)\} = x(-t)$$

  两次FT对应时间反转，四次FT才回到原信号，FT可视为时频平面上的90°旋转，并可进一步推广到任意角度旋转的分数FT。对于(实)对称函数，两次FT即可回到原信号。
• 卷积定理

  $$\mathcal{F}\{f*g\} = \mathcal{F}\{f\} \mathcal{F}\{g\}$$

  信号卷积的FT = 信号FT后相乘；信号相乘的FT = 信号FT后卷积

  $$\mathcal{F}\{f g\} = \mathcal{F}\{f\} * \mathcal{F}\{g\}$$

  注：后者只针对普通频率$f$形式成立，使用角频率会有$\frac{1}{2\pi}$因子
• 相关定理：

  $$\mathcal{F}\{f \star g\} = \overline{\mathcal{F}\{f\}} \mathcal{F}\{g\}$$

  信号相关的FT = 信号FT取共轭后相乘，相比卷积多了后者多了共轭。在自相关情况下即为维纳-辛钦定理：平稳信号的功率谱密度是其自相关函数的傅立叶变换。

  $$\mathcal{F}\{f \star f\} = |\mathcal{F}\{f\}|^2$$

• 帕塞瓦尔(Parseval)定理：

  $$\displaystyle \int f(t)\overline{g(t)} dt = \int F(f)\overline{G(f)} df$$

  $$\displaystyle \int |x(t)|^2 dt = \int |X(f)|^2 df$$

  能量守恒
• 泊松求和公式：

  $$\sum_n x(n) = \sum_k X(k)$$

  将普通函数的离散求和变为其傅里叶变换的离散和。
  定义$f(t) = \sum_n x(t+n)$，即$x(t)$以1为单位平移求和：$f(t)$为周期性函数(周期为1)，进行傅里叶级数展开的系数为：

  $$\begin{aligned} \alpha_k &= \int_0^1 f(t) e^{-i 2\pi k t} dt = \int_0^1 \sum_n x(t+n) e^{-i 2\pi k t} dt\\ &= \sum_n e^{i 2\pi k n} \int_n^{n+1} x(t) e^{-i 2\pi k t} dt \\ &= \int x(t) e^{-i 2\pi k t} dt = X(k) \end{aligned}$$

  $f(t) = \sum_n x(t+n) = \sum_k \alpha_k e^{i 2\pi k t} = \sum_k X(k) e^{i 2\pi k t}$，取$t=0$得证。
  通过引入周期性函数$f(t)$，将傅里叶级数与傅里叶变换结合：$f(t)$傅里叶级数展开系数对应$x(t)$傅里叶变换(在离散频率处取值)。这种非周期函数通过周期性平移叠加得到周期性函数的操作是傅里叶分析中的操作，尤其是当平移周期大于信号长度小时，就对应信号的周期性延拓。
• 导数定理：

  $$\mathcal{F}\{x'(t)\} = i\omega X(\omega)$$

  $$\mathcal{F}\left\{x^{(n)}(t)\right\} = (i\omega)^n X(\omega)$$

• 积分：

  $$\mathcal{F}\left\{\int_{-\infty}^t x(\tau) d\tau \right\} = \frac{1}{i\omega} X(\omega) + \pi X(0) \delta(\omega)$$

在高维空间傅里叶变换定义变为矢量形式$\int_{\R^n} f(\bm{x})e^{-i2\pi \bm{k} \cdot \bm{x} } d\bm{x}$，相关性质也扩展为矢量形式，平移变为矢量平移，缩放变为线性变换(矩阵乘法)。

离散时间变换 DTFT

从傅里叶变换角度看傅里叶级数，相当于是以$1/T_s$为间隔对频率采样后做逆变换：

$$x(t) = \int X(f) e^{i 2\pi f t} df \xrightarrow{f=k/T_s} \sum_{-\infty}^{\infty} \frac{1}{T_s}X(k/T_s) e^{i \frac{2\pi k}{T_s} t} = \sum_{-\infty}^{\infty} \alpha_k e^{i \frac{2\pi k}{T_s} t}$$

其展开系数：

$$\alpha_k = \frac{1}{T_s}X(k/T_s) = \frac{1}{T_s}\int_{T_s} x(t) e^{-i \frac{2\pi k}{T_s} t} dt$$

与之相对的，以$T_s$为间隔对时间进行采样后的傅里叶变换为：

$$X(f) = \int x(t) e^{-i 2\pi f t} dt \xrightarrow{t=nT_s} \sum_{-\infty}^{\infty} T_s x(nT_s) e^{-i 2\pi f ~ nT_s} = \sum_{-\infty}^{\infty} x[n] e^{-i 2\pi f ~ nT_s}$$

最终对于离散时间变换DTFT有：

$$\boxed{X_{\frac{1}{T_s}}(f) = \sum_{-\infty}^{\infty} x[n] e^{-i 2\pi f ~ nT_s}, ~~~ x[n] = T_sx(nT_s) = T_s\int_{\frac{1}{T_s}} X_{\frac{1}{T_s}}(f) e^{i 2\pi f n T_s} df}$$

另一种常见的定义方式是：

$$\boxed{X_{\frac{1}{T_s}}(f) = \sum_{-\infty}^{\infty} x_n e^{-i 2\pi f ~ nT_s}, ~~~ x_n = x(nT_s) = T_s \int_{\frac{1}{T_s}} X_{\frac{1}{T_s}}(f) e^{i 2\pi f n T_s} df}$$

两种定义形式上完全一致，区别在于$x[n]$变为$x_n$。
最后，对于离散样本(信号采样)，一个常见做法是用采样频率$f_s = \frac{1}{T_s}$对频率进行归一化$f/f_s$，相应的，信号时间由采样间隔归一化$nT_s/T_s$。最终信号“时间”变为整数(个样本)，采样间隔为1(个样本)，DTFT频谱周期也变为1。且对于归一化频率，更常见的是角频率形式，频谱周期中的$\pi$指示了频率的归一。

$$X_1 (f) = \sum_{-\infty}^{\infty} x[n] e^{-i 2\pi f n}, ~~~ x[n] = \int_1 X_1(f) e^{i 2\pi f n} df$$

$$X_{2\pi}(\omega) = \sum_{-\infty}^{\infty} x[n] e^{-i \omega n}, ~~~ x[n] = \frac{1}{2\pi}\int_{2\pi} X_{2\pi}(\omega) e^{i \omega n} d\omega$$

• Parseval定理：

  $$\begin{aligned} \sum_{-\infty}^{\infty} \Big|x[n]\Big|^2 &= \sum_{-\infty}^{\infty} x[n]\overline{x[n]} = \sum_{-\infty}^{\infty} \left[ T_s\int_{\frac{1}{T_s}}X_{\frac{1}{T_s}}(f)e^{i2\pi f n T_s} df \right]~\overline{x[n]}\\ &= T_s\int_{\frac{1}{T_s}} df ~ X_\frac{1}{T_s}(f) ~ \overline{\sum_{-\infty}^{\infty} x[n] e^{-i2\pi f n T_s}} = T_s\int_{\frac{1}{T_s}} X_\frac{1}{T_s}(f) \overline{X_\frac{1}{T_s}(f)} df\\ &= T_s\int_{\frac{1}{T_s}} \Big|X(f)\Big|^2 df \end{aligned}$$

  相比连续序列，这里频域积分对于单个周期的，且多了系数$T_s$。

DTFT的周期性
根据泊松求和公式有

$$X_{\frac{1}{T_s}}(f) = \sum_{n=-\infty}^{\infty} T_s x(nT_s) e^{-i 2\pi f ~ nT_s} = \sum_{k=-\infty}^{\infty} X(f-\frac{k}{T_s})$$

上式表明，对$x(t)$采样后傅里叶变换的频谱$X_{\frac{1}{T_s}}(f)$，相当于$X(f)$以$\frac{1}{T_s}$为单位无限平移求和，或者说将$X(f)$切分为$\frac{1}{T_s}$的片段进行折叠求和，并周期性延拓。采样后DTFT得到的频谱为周期$\frac{1}{T_s}$的周期函数，对应于直接FT的周期性叠加。显然，如果$x(t)$的频带宽度超过频谱周期$\frac{1}{T_s}$，高频成分将被叠加入低频部分，使频谱失真，进而在信号恢复时噪声所谓混叠(aliasing)。采样率的选择(Nyquist采样率)对于减轻混叠效应很重要，此外通常会在信号采样前使用低通滤波抑制高频成分(采样后混叠就去不掉了)。

傅里叶级数是周期性函数的频域分解，时域具有周期性，频域中离散；DTFT可视为傅里叶级数的频域对偶，在时域离散，频域为周期性。下图展示了傅里叶变换(左上)、傅里叶级数(右上)、连续时间傅里叶变换(左下)及离散傅里叶变换(右下)。图中左下可看到采样后，连续信号频谱的高频被混入低频区间，并周期性延拓。

• 抽取(Decimation)：$y[n] = x[nM]$，M为整数
  每M个样本取一个，构成新序列。相当于时间压缩，同时采样间隔由T_s变为MT_s，周期将由$\frac{1}{T_s}$变为$\frac{1}{MT_s}$，因此在缩放的基础上还多了频谱折叠。

  $$x[nM] \leftrightarrow \frac{1}{M} \sum_0^{M-1} X_{\frac{1}{T_s}}\left(\frac{f-m}{M}\right)$$

• 补零：当n/M为整数$y[n] = x[n/M]$，不能整除则$y[n] =0$
  相邻样本间插入$M-1$个零，构成新序列。相当于时间拉伸，同时采样间隔由T_s变为T_s/M，周期将增大M倍，不存在折叠。

  $$y[n] \leftrightarrow X_{\frac{1}{T_s}}\left(Mf\right)$$

周期性数据
当样本为周期函数(周期为$N$)，对应DTFT取离散值，只在$f=\frac{k}{NT_s}$取值非0(值发散)，考虑到DTFT本身为周期函数，对应的独立谱值只有$\frac{1}{T_s}/\frac{1}{NT_s} = N$个，而单个周期内的取值就对应离散傅里叶变换DFT。

$$X_{\frac{1}{T_s}}(f) = \sum_{-\infty}^{\infty} x[n] e^{-i 2\pi f ~ nT_s} \xrightarrow{f=k/NT_s} \sum_{-\infty}^{\infty} x[n] e^{-i 2\pi \frac{k}{NT_s} ~ nT_s} = \sum_{-\infty}^{\infty} x[n] e^{-i 2\pi \frac{k}{N} n}$$

$x[n]$及$e^{-i 2\pi \frac{k}{N} n}$均为周期$N$的函数，求和可切分为先在周期内求和，再对各周期求和。将单周期内样本记为$x_n=x(nT_s)=\frac{1}{T_s}x[n]$，对应求和记为$X_k$。

$$X_k = \sum_{n=0}^{N-1} x_n e^{-i 2\pi \frac{k}{N} n}$$

$$X[k] = X_{\frac{1}{T_s}}\left(\frac{k}{NT_s}\right) = \sum_{n'=-\infty}^{\infty} T_s X_k = T_s X_k~\delta(k - fNT_s)$$

$$X_{\frac{1}{T_s}}(f) = \sum_{k=-\infty}^{\infty} X[k] = \frac{1}{N} \sum_{k=-\infty}^{\infty} X_k ~\delta(f-\frac{k}{NT_s})$$

对应的逆变换：

$$x_n = \frac{1}{T_s} x[n] = \int_{\frac{1}{T_s}} X_{\frac{1}{T_s}}(f) e^{i 2\pi f n T_s} df = \frac{1}{N} \sum_{k=0}^{N-1} X_k e^{i 2\pi \frac{k}{N} n}$$

最终：

$$X_k = \sum_{n=0}^{N-1} x_n e^{-i 2\pi \frac{k}{N} n}, ~~~ x_n = \frac{1}{N} \sum_{k=0}^{N-1} X_k e^{i 2\pi \frac{k}{N} n}$$

注意，这里离散变换与连续傅里叶值在取值上关系为$X_k = \frac{X(f)}{T_s} = X(f)f_s$

一般数据
对于一般的非周期样本，$X_{\frac{1}{T_s}}(f)$为连续的周期性函数，此时可对其进行采样，假设每个周期采样数为$N$：

$$X_N[k] = X_{\frac{1}{T_s}}\left(\frac{k}{NT_s}\right) = \sum_{-\infty}^{\infty} x[n] e^{-i 2\pi \frac{k}{N} n}$$

由于$e^{-i 2\pi \frac{k}{N} n}$周期为$N$，上述求和可进行折叠：

$$\begin{aligned} X_N[k] &= \sum_{m=-\infty}^{\infty} \sum_{n=0}^{N-1} x[n-mN] e^{-i 2\pi \frac{k}{N} n} \\ &= \sum_{n=0}^{N-1} \sum_{m=-\infty}^{\infty} x[n-mN] e^{-i 2\pi \frac{k}{N} n} \\ &= \sum_{n=0}^{N-1} x_N[n] e^{-i 2\pi \frac{k}{N} n} \end{aligned}$$

上述变换为DFT，其中$x_N[n]=\sum_{m=\text{-}\infty}^{\infty} x[n~\text{-}~mN]$，对应于$x[n]$以$N$为单位无限平移求和所构造的周期性函数，或者将$x[n]$切分为长度为N的片段折叠求和，并周期性延拓。而上述变换表明：对频谱$X_{\frac{1}{T_s}}(f)$的采样$X_N[k]$，对应于时域样本折叠求和并周期性延拓(周期性数据)，之后进行离散傅里叶变换DFT。即离散信号周期延拓的DFT对应于对离散信号DTFT频谱的采样。

这里也可以看到采样与周期延拓的对偶：一个域中的采样(离散化)对应另一个域中的周期延拓(周期性)。时域信号FT为其频谱，而对时域信号采样的DTFT对应其频谱周期延拓；DTFT频谱逆变换可得到信号采样，对DTFT频谱采样的逆DFT又对应于信号采样的周期延拓。直观理解，以时域信号$\cos(2\pi f t + \phi)$为例，经过离散采样变为$\cos(2\pi f nT_s + \phi)$，此时$f$与$f + \frac{k}{T_s}$信号值完全相同，无法区分，连续信号并不存在该问题。对应到频域，意味离散信号频谱具有$\frac{1}{T_s}$的周期性。

采样、窗口与失真

采样定理
最大频率(频带上限)为B的连续信号可由以2B频率采样得到的离散序列完全决定。该定理被称为香农采样定理或奈奎斯特-香农(Nyquist-Shannon)采样定理。

前面已介绍，采样序列DTFT频谱为原信号频谱的无限平移求和，周期为采样频率$f_s = \frac{1}{T_s}$。对基带信号(零频率附近)，频谱范围[-B, B]2倍于最大频率。当采样频率超过2倍最大频率，频率范围小于平移周期，周期性平移求和时频谱不存在重叠，截取DTFT频谱基带周期即为原信号频谱：$X(f) = X_{\frac{1}{T_s}}(f) {\rm rect}(\frac{f}{f_s}) = \sum_{n=\text{-}\infty}^{\infty} x(nT_s) ~ T_s~{\rm rect}(T_sf) e^{-i 2\pi n T_sf}$，对其傅里叶逆变换有：

$$x(t) = \sum_{n=-\infty}^{\infty} x(nT_s) ~ {\rm sinc}\left(\frac{t-nT_s}{T_s}\right)$$

即将每个采样点$x(nT_s)$乘以对应位置的Sinc函数，加权求和即可恢复原始连续信号。该公式被称为惠特克—香农(Whittaker–Shannon)插值公式。

根据采样定理，当采样频率高于2倍的模拟信号最高频率，采样序列就可不失真的代表原信号，临界频率2B被称为信号的奈奎斯特采样率(Nyquist rate)；相对的，对给定的采样频率$f_s$，信号不失真需要其频带上限小于$f_s/2$，而临界频率$f_s/2$被称为采样系统的奈奎斯特频率(Nyquist frequency)。

当采样频率超过Nyquist速率时，对信号的重建并不会有影响；当采样频率低于Nyquist速率则将出现混叠。高于采样频率一半的信号会与低于采样频率一半的信号混淆，两者虽然频率不同，但在给定采样频率下的采样值完全一样，无法做出区分。实信号的幅值频谱关于零点对称，经过采样后，频谱折叠为周期性。仅考虑非负频率，在一个周期$[0, f_s]$内，$[\frac{1}{2}f_s, f_s]$对应于$[\text{-}\frac{1}{2}f_s, 0]$，从而与$[0, \frac{1}{2} f_s]$关于奈奎斯特频率$\frac{1}{2}f_s$对称，这种对称性被称为“折叠”(folding)。频率$f$与$f_s~\text{-}~f$的信号将在采样频率下相混淆，与其他周期内对应频率也都互为alias。对于复信号，由于正负频率不存在对称性，因此不存在频谱“折叠”现象，频率$f$只与其他周期内对应频率$f+nf_s$构成alias。

日常生活中，注视高速旋转的轮子时，会产生静止甚至反向旋转的错觉，就是人眼“采样频率”过低所引起的混叠。理论上，只要轮子旋转速度(信号频率)超过了人眼视觉停留刷新频率(10Hz左右)就会出现错觉：当轮子在视觉停留时间内转了大半圈(频率超过采样频率一半)或者整数圈多一点，则主观会认为轮子每次反向旋转了一点，从而产生缓慢倒转的错觉；当轮子大致在视觉停留时间内刚好转整数圈，则主观会认为轮子保持静止。

采样定理的推广
上述采样定理只描述了均匀采样，且只针对频率从零开始的基带(baseband)/低通(lowpass)信号。对于非均匀采样，Nyquist条件同样成立；而对于带通(bandpass)信号，在信号频带范围已知的前提下，主动利用混叠效应可以极大降低采样率而不影响信号重建。

• 非均匀采样
  均匀采样在信号重建时算法实现上比较简单，但却并非必要，只要平均采样频率满足Nyquist条件，非均匀采样也可实现信号无损重建；
• 非基带信号(带通采样)
  采样序列DTFT频谱为原信号频谱的无限平移求和，周期为采样频率$f_s$，无损获取原频谱只需其频率范围小于平移周期，平移时不存在重叠。基带信号频率范围为[-B, B]，对应条件为频谱落入$(\text{-}\frac{1}{2}f_s, \frac{1}{2}f_s)$。带通信号为对称区间$(\text{-}f_H, \text{-}f_L) \cup (f_L, f_H)$，对应要求频谱由$(\text{-}\frac{n+1}{2}f_s, \text{-}\frac{n}{2}f_s) \cup (\frac{n}{2}f_s, \frac{n+1}{2}f_s)$覆盖，$n$为非负整数。考虑到对称性这里只关注非负频率，即要求$(\frac{n}{2}f_s, \frac{n+1}{2}f_s)$覆盖信号的非负频带$(f_L, f_H)$，从而采样频率$\frac{2}{n+1}f_H \le f_s \le \frac{2}{n}f_L$。
  对带通信号，$n$可能有多个取值，取0便对应基带情况结论，即要求采样频率至少2倍于信号频率上限。频率随$n$增加而降低，但$\frac{2}{n+1}f_H \le \frac{2}{n}f_L$限制了$n \le \frac{f_L}{f_H-f_L}$，因此$n = \lfloor\frac{f_L}{f_H-f_L}\rfloor$为极限情况，对应频率下限$\frac{2}{n+1}f_H = \frac{2 f_H}{\lfloor f_H/(f_H-f_L)\rfloor} \gtrsim 2(f_H~\text{-}~f_L)$，即采样频率下限接近于2倍带宽，而非2倍信号频率上限。此时相当于将信号作为其基带附近的混叠信号(alias)，按照基带情况进行采样。通过主动利用低频的混叠信号，可大幅降低采样率，减少资源消耗。
  带通滤波需要预先知道信号的频带范围，以从众多混叠信号中确定实际信号频段。因此带通采样需要配合带通滤波使用，用以移除非目标频段信号的干扰。而且，实际中通常并不会追求采样频率的下限，而是适当放宽，为抗混叠滤波留出操作空间。
  最后，除了连续频带信号，还可进一步的扩展到信号频率分布在多个不连续子频带的情况，此时带宽对应变为实际覆盖的有效带宽。
• 非基带+非均匀采样
  实现信号无损重建，平均采样率至少只需要是信号(有效)带宽的二倍，前提是知道具体的频率区间，如果不知道则采样率需要提升2倍(?)。

最后，Nyquist条件是无损重建的充分条件，但并非必要条件，如果信号存在额外的限制条件，采样频率下限是可以打破。比如，对于有效带宽为EB的频域稀疏信号，即信号频率分布在不连续的子频带，而非连续的频带，此时前面带通信号的技巧不再适用，因此原则上采样频率需要是频率上限的2倍。但利用压缩感知技术，则可用略低于2倍有效带宽的频率进行采样，并实现无损重建。不过在这种情况下，简单的香农插值公式就不在适用，信号的重建需要借助线性规划。此外，考虑到离散信号到数字信号的量化(Quantization)过程，信号重建的误差存在下限，进而对采样频率的要求也可适当放松(无需强求无损)。

窗口函数
采样定理虽然表明有限带宽的函数可以采样而不丢失信息，但根据不确定性原理，在频域有限意味着信号在时域无限延伸，实际处理中却需要将信号限制在有限时间段内，这将引入额外失真，被称为频谱泄露。而通过调整用于截取信号的窗口函数，可以平衡频谱泄露的具体影响。

窗口函数简单说就是仅在有限的区间(窗口)内非零的函数，通常关于区间中心呈对称分布，且在中心附近取值最大，向两侧逐渐衰减，最简单的就是矩形窗口。作为时间的函数，常见窗口函数大致可分为幂窗、三角窗、指数窗三类：幂窗为时间的幂函数，如矩形、三角形、抛物线等；三角窗为时间的三角函数，包括汉宁窗、海明窗、图基窗、平顶窗等；指数窗则为时间的指数形式，如高斯窗、泊松窗。

从时域角度理解，任意函数与窗口函数相乘后，将仅保留窗口内的数值。在频谱分析时，会将截取的片段作为周期函数的单个周期进行DFT。对于周期信号，简单的信号截取(矩形窗)，如果刚好覆盖整数周期(相干采样)，则延拓得到的时域信号与原信号一致，并不存在频谱泄露。但如果截取的并非整数周期(非相干采样)，则延拓时边界处将存在跳变，而脉冲信号(跳变)对应延展的频谱。下图展示的是用长度1s的窗口(对应频谱分辨率1Hz)，截取50Hz和50.5Hz正弦信号后的频谱，可以明显看到频谱泄露。窗口函数通过压低边界值，对延拓边界进行平滑，避免了跳变，进而减少频谱泄露。这正是引入窗口函数的主要目的，通过适当的窗口函数对信号进行调制，可减轻频谱泄露对后续分析的影响。

从频域角度理解，根据卷积定理，信号乘以窗口函数后，其频谱为原信号频谱与窗口函数频谱进行卷积操作。而窗口函数的频谱可理解为对频率为0的余弦波$\cos(2\pi 0 t)$加窗后的傅里叶变换，因此其频谱偏离零频率的情况可用于理解窗口的频谱泄露效应。通常窗口函数的频谱表现为位于零点的主瓣及向高频延伸的旁瓣，原本集中于零点处的频谱被分散到较宽的频带中(泄露)，如下图所示。

理想中的窗口函数频谱是主瓣宽度窄、旁瓣幅值低且衰减快，实际两者并不可兼得：较窄的主瓣通常伴随较高的旁瓣，这种窗口对于频率识别精度高，但弱信号容易被旁瓣遮蔽，幅值容许范围较窄(高分辨率、低动态范围)；相对的，较宽的主瓣结合较低的旁瓣，这种窗口对幅值差别宽容度大，但对于频率分辨率低，频率接近的成分容易因展宽而无法分辨(高动态范围、低分辨率)。具体的，矩形窗主瓣窄但旁瓣高，属于高分辨率、低动态范围；平顶窗、布莱克曼窗主瓣宽但旁瓣低且衰减快，属于高动态范围、低分辨率；汉宁窗、海明窗则介于两者之间，在对频率分辨率有要求的窄带分析中较为常见。

窗口函数的量化属性主要有(等效)噪声带宽、最高旁瓣以及旁瓣衰减。其中噪声带宽为窗口频谱的等效展宽，代表了整体的泄露情况，主要决定于主瓣宽度。而随机噪声信号产生的噪声水平(noise floor)正比于窗口函数的噪声带宽，这会影响信号分析。比如高动态范围的窗口理论上有助于识别弱信号，但当存在随机噪声时，高动态范围窗口(噪声带宽宽)通常对应更高的噪声水平，最终影响对于弱信号的灵敏度。而低动态范围的窗口由于有更低的噪声水平，反而有助于提升信噪比(但又会受栅栏效应影响)。又比如对于爆发信号，信号峰值集中于窗口一端，矩形窗之外的窗口函数都将压制大部分的信号能量，降低信噪比。根据窗口函数对于信号和(加性)噪声的不同响应，可在信号处理时产生额外的分析增益或损失，实际中应根据信号性质及最终需求进行选择。

主瓣宽，信号强度准，但噪声水平高；主瓣窄，噪声水平低，但信号强度不准 ^ref

频谱失真
频谱分析中会先进行信号采样，之后对截取的信号样本周期性延拓，并进行DFT变换。这其中涉及采样、截断和周期延拓，都将对频谱产生影响。

• 信号混叠(aliasing)：源于采样，由过低的采样频率引入；
• 频谱泄露(spectral leakage)：源于截断，由非周期截断引入；
• 栅栏效应(picket-fence effect, scalloping loss)：源于频域采样(时域延拓)。

混叠和泄露前面已介绍，虽然都会使频谱失真，但窗口函数导致的频谱泄露是局部的频谱展宽与界限模糊；采样导致的混叠则是频谱折叠对应的整体上的、周期性的模糊。增加窗口宽度及选择合适的窗口函数是抑制频谱泄露的关键，避免混叠则需要提升采样率。

这里主要介绍下栅栏效应：时域信号的周期性延拓对应于频域采样，采样间隔(频率分辨率)为时域窗口宽度的倒数。设采样频率为$f_s$，采样数为$N$，信号的非周期截断意味截取时长$N/f_s$与信号周期不匹配，对应于信号频率与频谱的频率分辨率$f_s/N$不匹配，不属于被采样的频率，只能用相邻频率的幅值进行近似，这就是栅栏效应。因为是通过有限的采样谱线(栅栏的缝隙)去近似完整的频谱，位于谱线间的频率，对应的幅值只能近似估计。

对于周期性信号，理论上偏离实际频率幅值就为零，但考虑到非周期性截断所引入的频谱泄露，相邻频率的幅值并非0，但会低于真实频率幅值。延用前面频谱泄露的例子，1s的窗口对应频率分辨率1Hz，对于50.5Hz的信号只能给出在50Hz和51Hz处的谱值(来自于频谱泄露)，而无法给出50.5Hz处的峰值，这就是栅栏效应，也被称为扇形损失(泄露呈扇形)。显然频谱泄露越严重，相邻谱线与真实频率幅值偏差小，栅栏效应越不明显。此外，当信号频率刚好位于谱线中间时，扇形损失最显著。

栅栏效应可在不增加数据前提下通过“补零”进行改善。前面已介绍，时域信号周期性延拓 + DFT，对应于DTFT频谱的采样，而在输入序列末尾补零可调整采样的位置。将${x_n}$由长度N补零到M(>N)的${x_m}$，对其进行DFT有：

$$\sum_{0}^{M-1} x_m e^{-i 2\pi\frac{k}{M} m} = \sum_{0}^{N-1} x_m e^{-i 2\pi\frac{k}{M} m}, k\in[0, ..., M-1]$$

频率采样位置由$\frac{k}{N}$变为$\frac{k}{M}$，采样点数由N变为M。即补零可以增加栅栏的缝隙，从而直接得到原本被跳过的频率分量。对于已知的频率，通过选择适当的M可使目标频率不被遗漏，且当M为N整数倍时，新的谱线包含补零前的谱线。此外FFT算法在输入序列长度为$2^n$时效率最高，选择适当的M可加快计算。

补零降低了频域采样间隔，看似增加了对频率的分辨精度，但实际频率分辨率保持不变。从频域采样角度理解，补零增加了对截断信号DTFT的采样，最终也只是逼近原信号DTFT连续谱，而后者的频率分辨率始终为信号有效时长的倒数。从窗口截断角度理解，频谱分辨率受限于频谱泄露导致的谱线展宽，展宽(泄露)随窗口宽度增加而减小，对应于频率分辨率随信号时长增加而增加，数据补零并没有增加窗口的有效宽度，也就不能改善频谱泄露。因此补零虽然在效果上可以平滑频谱，但其整体包络线对应的依然是信号截断导致的频谱泄露(DTFT连续频谱)。从时域采样角度理解，补零增加了采样点数，但有效信号时长保持不变，只相当于增加了平均采样率 $f'_s=\frac{M}{N}f_s$，从而最终频域分辨率 $\frac{f'_s}{M}=\frac{f_s}{N}$ 保持不变。而从信息论角度理解，补零没有增加输入信息，频谱分辨率的提高只能在满足采样定理的条件下增加时域采样长度来实现。

下图中，输入信号为50Hz和50.5Hz两个频率的正弦波，1s采样对应频率分辨率为1Hz，无法分辨出两个频率，也无法给出50.5Hz处的幅值。通过补零增加一倍的采样点，可以给出50.5Hz处的幅值，改善了栅栏效应，但频谱的整体展宽趋势不变，只是对原频谱进行了更密集的采样。而11s采样则可以明显看到50Hz和50.5Hz的两个频率峰，不过50.5Hz处幅值由于栅栏效应存在低估(同样可通过补零改善)。

窗口对称性
对于傅里叶变换有$x(\text{-}t) \leftrightarrow X(\text{-}\omega)$，因此对偶函数有$X(\omega)=X(\text{-}\omega)$，同时对实信号又有$X(\text{-}\omega)= \overline{X(\omega)}$，最终对于实数域的偶函数有$X(\omega)=\overline{X(\omega)}$，即其频谱为实数。以矩形窗为例，$[-\frac{T}{2}, \frac{T}{2}]$的窗口函数$\text{rect}\left(\frac{t}{T}\right)$，傅里叶变换为实函数$T\text{sinc}\left(T \frac{\omega}{2\pi}\right)$。但当将窗口范围平移至$[0, T]$，傅里叶变换将变为$T\text{sinc}\left(T \frac{\omega}{2\pi}\right)e^{-i \omega \frac{T}{2}}$，为复值函数，取值仅在$f=\frac{k}{T}$时为实数。

对于经过采样的(离散)窗口函数$w[n]$，当其关于零点对称，则DTFT频谱$X(\omega)$为实数。将窗口范围$[\text{-}\frac{N}{2},\frac{N}{2}]$平移$\frac{N}{2}$到DFT窗口$[0, N]$，有$X'(\omega)=e^{-i \omega \frac{N}{2}}X(\omega)$，即其DTFT频谱只在$\frac{k}{N}$频率点处为实数，其余频率谱值均为复数。而[0,N]区间序列长度为N+1，DFT对应频率间隔$\frac{1}{N+1}$，对应频率点为$\frac{k}{N+1}$，谱值为复数。

因此，实际计算DFT时会舍弃最后一个样本(考虑到w[N]=0舍弃的是最后的零)，取$[0, N)$的样本计算N点DFT，这会影响窗口函数的频谱泄露，但能使得采样频谱为实数。舍弃最后样本使窗口失去了对称性，但适合周期性延拓，而通过周期性延拓可以得到关于零点对称的周期函数，从这个角度也可以更直观的理解其DFT系数为实数。这种比对称窗口少一个样本的窗口也因此被称为周期性窗口或DFT对称(DFT-symmetric, DFT-even)窗口。不过DFT系数之外的频率依然对应复谱，前面窗口函数的频率响应，就是通过补零计算DFT，并对复频谱取模得到。

最后，除了在频谱分析时截断信号，窗口函数还常用于滤波设计，通过对理想的脉冲响应加窗得到有限冲激响应(Finite impulse response, FIR)滤波器。不过滤波器设计中使用的是对称窗口，而非不对称的周期性窗口。此外，在统计分析中也会用到窗口函数，通过加权限制用于分析的数据范围，在贝叶斯分析中，窗口函数通常被称为“核函数”。

离散傅里叶 DFT

函数等间隔采样的有限序列 $\xleftrightarrow{DFT}$ 函数DTFT的等间隔采样(采样数相同)
如果将原序列视为有限区间非零的函数，其DTFT为连续周期函数，DFT为单个周期内的离散采样；如果将原序列视为周期性延拓函数的单个周期，则其DTFT为离散周期函数，DFT对应单个周期内的所有非零值。

$$\boxed{X_k = \sum_{n=0}^{N-1} x_n e^{-i\frac{2\pi k}{N} n}, k \in [0, N -1]; ~~~ x_n = \frac{1}{N}\sum_{k=0}^{N-1} X_k e^{i\frac{2\pi k}{N} n}, n \in [0, N -1]}$$

这里时域的$n$对应于时间$t$，频域的$k$对应频率$f$。上述定义中因子$\frac{1}{N}$被放在了逆变换，是最常见的DFT定义形式，其它的还有将$\frac{1}{N}$放在正变换或者两者平分(幺正变换)。在上述定义形式下，对于同样长度的正弦信号，随着采样增加(N增加)，$X_k$会增加。对比傅里叶级数表达式，频域分解系数$\alpha_k$对应于$\frac{X_k}{N}$而非$X_k$，不会随采样增加改变。类似的，采样频率不变，时长增加(N增加)，$X_k$也增加；相反，N不变，时长增加(采样频率降低)，$X_k$不变(时长需要增加整数周期，以保证信号前后一致，且采样频率至少2倍信号频率)。

将序列$\{X_k\}, \{x_n\}$作为向量，上式还可表示为矢量形式：

$$\begin{pmatrix} X_0 \\ \vdots \\ X_k \\ \vdots \\ X_{N-1} \end{pmatrix} = \begin{pmatrix} 1& 1& 1& \dots& 1 \\ 1 & e^{-i \frac{2\pi}{N}}& e^{-i \frac{2\pi}{N} 2}& \dots & e^{-i \frac{2\pi}{N}(N-1)} \\ 1 & e^{-i\frac{2\pi}{N} 2}& e^{-i \frac{2\pi}{N} 4}& \dots & e^{-i \frac{2\pi}{N} 2(N-1)} \\ \vdots& \vdots& \vdots& \ddots& \vdots \\ 1& e^{-i \frac{2\pi}{N}(N-1)}& e^{-i \frac{2\pi}{N}2(N-1)}& \dots& e^{-i \frac{2\pi}{N} (N-1)^2} \end{pmatrix} \begin{pmatrix} x_0 \\ \vdots \\ x_n \\ \vdots \\ x_{N-1} \end{pmatrix}$$

$$\begin{pmatrix} X_0 \\ \vdots \\ X_k \\ \vdots \\ X_{N-1} \end{pmatrix} = \begin{pmatrix} w^0& w^0& w^0& \dots& w^0 \\ w^0& w^1& w^2& \dots & w^{N-1} \\ w^0& w^2& w^4& \dots & w^{2(N-1)} \\\vdots& \vdots& \vdots& \ddots& \vdots \\ w^0 & w^{N-1}& w^{2(N-1)}& \dots& w^{(N-1)^2} \end{pmatrix} \begin{pmatrix} x_0 \\ \vdots \\ x_n \\ \vdots \\ x_{N-1} \end{pmatrix}$$

$$\bm{X} = \Bigl( e^{-i\frac{2\pi}{N} k n} \Bigr)_{N\times N} ~ \bm{x} = \Bigl(w^{kn}\Bigr)_{N\times N} ~ \bm{x} = W\bm{x}$$

其中$w=e^{-i\frac{2\pi}{N}}$为N次单位根

离散傅里叶变换默认输出等于输入长度相同，即N个时间点对应N个频率点。调整输出长度对应于对输入序列进行补零或截断操作，输出长度为N的FFT通常被称为N点FFT。从对DTFT频谱采样角度理解，输出为离散序列DTFT的采样：采样点N等于输入序列长度L，对应于对输入直接周期性延拓后的DTFT，刚好对应N个离散频率；当采样点N大于输入序列长度L，会进行补零操作，相当于对原信号DTFT进行更密集的采样，频率分辨率不变但输出频点位置会改变；当采样点N小于输入序列长度L，从对DTFT频谱采样角度理解应该对输入做折叠，不过根据上面的DFT定义，实际采取的是将输入做截断，此时DFT对应的已不再是对完整输入DTFT的采样，而是对截断信号DTFT的采样，频谱不同，频率分辨率也会降低。对于平稳信号，在分辨率满足需求的前提下适当截断问题不大，可减少计算量。

DFT计算细节：

• 频谱采样：DTF时频域长度相同，N点时间采样对应N点频率采样，且频谱周期对应信号采样率$f_s$，具体采样频率为$f_k = \frac{k}{N} f_s$。
• 频率范围：频率$f=\frac{k}{N}f_s$，$k \in [0, N -1]$，对应的频率区间为$[0, f_s)$，并非基带$[-\frac{1}{2}f_s, \frac{1}{2}f_s]$，且最大频率为$\frac{N-1}{N}f_s$，并不能取到$f_s$。
• 基带频率：基于DTFT频谱的周期性，$[\frac{1}{2}f_s, f_s)$部分刚好对应基带区间$[-\frac{1}{2}f_s, 0)$。因此，可直接将后半部分频谱对应的频率记为相应的负频率(fftfreq)。最终，DFT频谱中第一个分量$X[0]$对应直流DC分量，之后的N-1个分量中，前(N-1)//2对应正频率，中间的N/2对应Nyquist频率，后(N-1)//2对应负频率。
• 频谱平移：进一步的可将负频率移至序列前面，或者说将零频率移至中间(fftshift, np.roll(arr, N//2))。Numpy中会将Nyquist频率移至最前面，对应$-\frac{1}{2}f_s$。考虑到$k$取N/2只有当N为偶数才可实现，最终偶数N对应的基带区间为$[-\frac{1}{2}f_s, \frac{1}{2}f_s)$，而奇数N对应的基带区间为$(-\frac{1}{2}f_s, \frac{1}{2}f_s)$。
• 单边频谱：对实信号，频谱具有共轭对称性(功率谱具有对称性)，可仅保留正频谱。同样由于Nyquist频率只有N为偶数才能取到，最终偶数N对应区间$[0, \frac{1}{2}f_s]$，奇数N对应区间$[0, \frac{1}{2}f_s)$。考虑到能量守恒，功率谱取值需乘以2，零频率及Nyquist频率没有负频率对应，并不需要变，具体可参考功率谱部分介绍。

最后再强调一遍，实信号双边谱具有共轭对称性，但计算中双边谱的数组并非中心对称！而是X[0]对应零频率，剩余部分中心对称！且零频率和Nyquist频率对应频谱必须是实数，其余部分可为虚数(共轭对称)。

spec = np.random.randn(100)
spectrum = np.r_[spec, spec[::-1]]
singal = np.fft.ifft(spectrum)
plt.plot(singal.imag, '.')

spectrum = np.r_[spec, spec[1:][::-1]]
singal = np.fft.ifft(spectrum)
plt.plot(singal.imag)
plt.show()

DFT基本性质：

• 零点：$X[0]=\sum_{0}^{N-1} x_n$ 直流DC分量
• 不确定性原理：$\Delta f = \frac{1}{N\Delta t}, ~~ \Delta t \Delta f = \frac{1}{N}$
  频率分辨率(采样间隔)为输入序列时长倒数，时频域分辨率不可兼得
• 线性：$\mathcal{F}\{x + y\} = \mathcal{F}\{x\} + \mathcal{F}\{y\}, \mathcal{F}\{a x\} = a\mathcal{F}\{x\}$
• 反转：$\{x_{N-n}\} \xleftrightarrow{} \{X_{N-k}\}$ 　　 时间反转对应频率反转
• 平移：$\{x_n e^{i2\pi\frac{n}{N}l}\} \xleftrightarrow{} \{X_{k-l}\}$ 　 时域的频移对应频域的平移
  　　　$\{x_{n-l}\} \xleftrightarrow{} \{X_k e^{-i 2\pi \frac{k}{N} l}\}$　时域的时移对应频域的相移
• 共轭：$\{\overline{x}_{n}\} \xleftrightarrow{} \{\overline{X}_{N-k}\}$
  　　　对于实信号$x_n \in \R$，有$X_k = \overline{X}_{N-k}$
• 帕塞瓦尔(Parseval)定理：$\sum_{n=0}^{N-1} x_n \overline{y}_n = \frac{1}{N}\sum_{k=0}^{N-1} X_k \overline{Y}_k$
  　　　　　　　　　　　 $\sum_{n=0}^{N-1} |x_n|^2 = \frac{1}{N}\sum_{k=0}^{N-1} |X_k|^2$
• 卷积：循环卷积 $x \circledast y = x * y_N = \sum_{l=0}^{N-1} x_{\tiny l}~y_{_{(n-l)~\text{mod}~N}} \xleftrightarrow{} X Y$
  　　　$x y \xleftrightarrow{} \frac{1}{N} X \circledast Y$ 注意多了$\frac{1}{N}$因子
• 相关：循环相关 $x \otimes y = x \star y_N = \sum_{l=0}^{N-1} x_{\tiny l}~y_{_{(n+l)~\text{mod}~N}}\xleftrightarrow{} \overline{X} Y$
  $x*y_N = \text{\footnotesize DTFT}^{-1}[\text{\footnotesize DTFT}(x)\text{\footnotesize DTFT}(y_N)] = \text{\footnotesize DFT}^{-1}[\text{\footnotesize DFT}(x_N)\text{\footnotesize DFT}(y_N)]$
  $x$为一般序列，$y_N$为周期$N$的序列，$\text{\footnotesize DTFT}(y_N)$为离散频谱，相乘时相当于同时对$\text{\footnotesize DTFT}(x)$采样，从而可表示为$x$周期求和后的离散傅里叶，这里$x_N$为序列$x$的周期求和。实际中，$y_N$通常为某个长度$N$序列的周期性延拓$\{y_{n~\text{mod}~N}\}$，而$x$长度通常不超过$N$，从而$x_N$也对应于$x$(补零后)的周期性延拓。
  序列经过周期性延拓后的周期性卷积被称为序列间的“循环卷积”，具体参考后面卷积部分，与之对应的还有“循环相关”。由于循环卷积局限于单个周期，因此两个序列延拓后的周期性卷积等于一个序列(单个周期外为0)与另一序列周期性延拓的(线性)卷积$x \circledast y = x * y_N$。

快速傅里叶 FFT

DFT默认的矩阵乘法计算复杂度为O(N²)，而变换矩阵的对称性与周期性使加速成为可能。具体实现有很多，但计算复杂度目前都在 O(NlogN) 量级，其中最著名的是 Cooley–Tukey 算法，核心思想是基于分治策略将长度N的序列变换缩减为更短序列的变换。

对于长度N(偶数)的序列$x_n$，将其离散傅里叶变换的奇偶项拆分有：

$$\begin{aligned} X_k &= \sum_{m=0}^{\frac{N}{2}-1} x_{2m} w_N^{2mk} + \sum_{m=0}^{\frac{N}{2}-1} x_{2m+1} w_N^{(2m+1)k}\\ &=\sum_{m=0}^{\frac{N}{2}-1} x_{2m} w_N^{2mk} + w^{k} \sum_{m=0}^{\frac{N}{2}-1} x_{2m+1} w_N^{2mk}\\ &=\sum_{m=0}^{\frac{N}{2}-1} x_{2m} w_{N/2}^{mk} + w^{k} \sum_{m=0}^{\frac{N}{2}-1} x_{2m+1} w_{N/2}^{mk}\\ &= X_{\rm even}[k] + w^{k}X_{\rm odd}[k], ~~~~ k=0, ..., N-1 \end{aligned}$$

其中 $X_{\rm odd}, X_{\rm even}$ 为$x_n$奇偶项各自的离散变换。虽然上式对$k\in [0, {\small N-}1]$均成立，但实际$X_{\rm even}, X_{\rm odd}$单个周期仅覆盖$k\in [0, \frac{N}{2}-1]$，而考虑到它们周期为$\frac{N}{2}$：

$$\begin{aligned} X_{k+\frac{N}{2}} &= X_{\rm even}\left[k+ {\small \frac{N}{2}}\right] + w^{k+\frac{N}{2}}X_{\rm odd}\left[k+ {\small \frac{N}{2}}\right]\\ &=X_{\rm even}[k] - w^{k}X_{\rm odd}[k] \end{aligned}$$

上述推导中利用了N次单位根的性质$w^{a+N} = w^a, w^{a+\frac{N}{2}} = -w^a, w^{a}_{N} = w^{a/b}_{N/b}$。最终序列长度N的DFT完全由长度N/2的DFT得到，如此递归计算复杂度可由O(N²)降至O(NlogN)。注意这里仅针对N为2的指数，对一般情况同样存在类似分解，不过在N为2的指数时FFT效率最高，因此通常N都会取为2的指数，计算时进行补零操作。
The execution time of fft depends on the length of the transform. Transform lengths that have only small prime factors (not greater than 7) result in significantly faster execution time than those that are prime or have large prime factors.

谱分析 Spectrum

物理上的“谱”(spectrum)的概念最初由牛顿提出，用于描述白光经过棱镜后的色散带。之后扩展为光强(功率)关于频率的函数，并最终扩展至任意信号的频域函数。作为频率的函数，频谱对应信号在频域分解时，不同频率成分的占比，反映出很多信号的内在特性。

能谱、功率谱

根据频率取值，频谱有离散谱和连续谱，而根据具体对的物理量，又有很多不同含义。

• 横轴频率取值：(离散)谱 v.s. 谱密度
  离散谱对应于周期性信号，频谱表现为离散的谱线，比如原子跃迁的吸收或辐射谱线就表现为离散谱。现实中更常见的是非周期性信号，对应连续的频率分布，也被称为谱密度(spectral density)。两者关系类似概率论中的离散随机变量的概率与连续随机变量的概率密度。在称呼上经常会混用，单独的(能/功率)“谱”所指代的可能是离散谱，也可能是连续的谱密度。
• 纵轴物理量：幅度谱、相位谱、能谱、功率谱
  单独的“频谱”，根据具体使用场景可用于指代上述各种谱，最常见的通常是指信号的功率谱(或幅度谱)。

复频谱
最直接的，对信号进行傅里叶变换就可得到频域表示$X(f)$，通常$X(f)$为复值函数，被称为复频谱。使用模长和幅角表示复值有$X(f) = A(f)e^{i\phi(f)}$，据此可以得到信号对应的幅度谱$A(f) = |X(f)|$和相位谱$\phi(f) = \text{angle}[X(f)]$，分别描述不同频率成分的信号幅度和初始相位，将所有频率成分以幅谱为权重、相谱为相位偏移，进行叠加就可得到对应的时域信号。
离散傅里叶变换(DFT) $X_k$、傅里叶变换(FT) $X(f_k)$与傅里叶级数(FS) $\alpha_k$对比：

$$X_k = \sum x_n e^{-i 2 \pi \frac{k}{N} n} = \sum x_n e^{-i 2 \pi f_k t_n}, ~~~~~ X(f) = \int x(t)e^{-i2 \pi f t} dt,~~~~~ \alpha_k = \frac{1}{T}\int x(t)e^{-i2 \pi f_k t} dt$$

这里$f_k = \frac{k}{N}f_s, ~t_n = \frac{n}{f_s} = nT_s$。$X_k$相比$X(f)$除了离散化之外，还少了$dt$，即采样间隔$T_s$：

$$\boxed{X_k = \frac{1}{T_s}X(f_k) = X(f_k)f_s; ~~~ \alpha_k = \frac{1}{N}X_k = \frac{1}{T}X(f_k)}$$

注意，对于平稳的信号或随机过程，虽然各频率成分振幅$\alpha_k$确定，但$X(f)$会随积分时长$T$增加而增加，对应$X_k$随采样点数$N$增加而增加。而如果信号时长也固定，则$X(f)$是确定的，但$X_k$依然会随采样率增加而增加！

能谱(Energy Spectral Density, ESD)
在介绍能谱前先引入任意时域信号“能量”的概念：

$$E = ⟨x(t), x(t)⟩ = \int |x(t)|^2 dt$$

注意，这里的能量是信号分析意义上的能量，而非严格物理意义上的能量。对于现实的物理过程，两者通常是成正比，比如对于电压或电流信号，直接平方积分显然不是能量，但如果考虑到系统电阻固定，则两者区别只在于比例常数。而一般地，在数学上，对于任意的抽象时域函数，上述定义并不具有物理意义上能量的含义，不过依据惯例，仍会类比物理过程，称之为“能量”。

所谓能谱就是信号“能量”关于频率的分布，根据Parseval定理：

$$\int |x(t)|^2 dt = \int |X(f)|^2 df$$

据此可以定义能谱密度：

$$\boxed{S_E(f) = |X(f)|^2}$$

进一步根据自相关定义：

$$|X(f)|^2 = \overline{X(f)}X(f) = \mathcal{F}\Big\{x(t) \star x(t) \Big\}$$

$$S(f) = \mathcal{F} \Big\{r_{xx}(t) \Big\} = \int r_{xx}(t)e^{- i 2\pi f t } ~ dt$$

显然能量(及能谱)的定义仅适用于能量积分收敛情况，即要求信号的总能量有限，被称为能量信号。能量信号傅里叶变换一般是存在的，常见的是短时脉冲或爆发等集中在有限时间段的信号。对于持续存在的信号，总能量发散，此时需要使用功率的概念。

功率谱(Power Spectral Density, PSD)
很多情况下，时域信号$x(t)$并非平方可积，傅里叶变换不存在，也就不存在通常意义上的复频谱或能谱。但如果截取有限长度信号$x_T(t)=x(t)w_T(t)$，其能量有限，存在傅里叶变换$X_T(f)$，对该截断信号$x_T(t)$可定义平均功率：

$$P_{x_T} = \frac{E_{x_T}}{T} = \frac{1}{T} \int |x_T(t)|^2 dt$$

当截取区间长度趋向无穷，$x_T(t)$的极限就是$x(t)$，因此原信号的“功率”可定义为上述平均功率在$T\rightarrow \infty$时的极限：

$$P = \lim_{T\rightarrow \infty} P_{x_T} = \lim_{T\rightarrow \infty} \frac{1}{T} \int |x_T(t)|^2 dt$$

功率(及功率谱)的概念需要上述极限存在(且非0)，此时$x(t)$被称为功率信号。注意，由于能量不一定是物理意义上的能量，这里“功率”也不一定对应物理意义上的功率，只是约定俗成的称呼(感觉这里power甚至可理解数学中的幂)。事实上，对于各态历经的随机过程，从统计角度理解，上述平均功率对应的其实是随机过程的方差(通常会提前减去均值)，而功率谱则对应不同频率成分所贡献的方差，具体可参考对随机过程的介绍。

功率非零意味$T\rightarrow \infty$时总能量发散，$x(t)$并非平方可积，但这并不影响截断信号$x_T(t)$傅里叶变换及上述极限的存在。根据Parseval定理：

$$\int |x_T(t)|^2 dt = \int |X_T(f)|^2 df$$

由此可定义功率谱密度(功率的频率分布)：

$$\boxed{S(f) = \lim_{T\rightarrow \infty} \frac{1}{T} |X_T(f)|^2}$$

进一步，根据自相关定理：

$$|X_T(f)|^2 = \overline{X_T(f)}X_T(f) = \mathcal{F}\Big\{x_T(t) \star x_T(t) \Big\}$$

$$S(f) = \lim_{T\rightarrow \infty} \frac{1}{T} \mathcal{F}\Big\{x_T(t) \star x_T(t) \Big\} = \mathcal{F}\Big\{ \lim_{T\rightarrow \infty} \frac{x_T(t) \star x_T(t) }{T} \Big\}$$

最终有：

$$\boxed{S(f) = \mathcal{F} \Big\{r_{xx}(t) \Big\} = \int r_{xx}(t)e^{- i 2\pi f t } ~ dt}$$

其中自相关函数$r_{xx}(t) \equiv \lim_{T\rightarrow \infty} \frac{x_T(t) \star x_T(t)}{T}$。注意这里自相关的定义多了对信号持续时间的平均。显然对于功率信号，通常的自相关$x(t) \star x(t) =\lim_{T\rightarrow \infty} x_T(t) \star x_T(t)$是发散的。基于该定义，求极限过程转移到了傅里叶变换之前。$x(t)$的傅里叶变换不存在，但$r_{xx}(t)$的傅里叶变换可以存在。

能谱 v.s. 功率谱
能谱适用于总能量有限的信号(平方可积)，被称为能量信号，其傅里叶变化一般存在，可直接根据信号傅里叶变换计算。功率谱则适用于平均功率有限的信号(极限存在且非0)，功率信号能量发散，其傅里叶变换通常不存在，可利用自相关函数的傅里叶变换得到功率谱。能量信号功率为0，功率信号能量发散，显然两者互斥，特定函数只能属于其中之一，也可能两者都不是(功率也发散)。能量信号常见的是短时脉冲或爆发，功率信号最常见的是周期性信号及随机信号。现实中随机噪声是不可避免的，观测数据会被视为随机过程的一次实现，而在分析信号或信噪比时通常会用功率谱。

能谱和功率谱都对应于信号“自相关”的傅里叶变换，但两种情况下自相关的定义是不同的，后者多了对时间区间的平均！能量信号通常持续时间有限，可通过傅里叶变换直接计算能谱，无需借助自相关。功率信号则是无限延伸，通常只能通过有限时间的观测对其功率谱进行估计，在平稳随机过程中，可借助截断信号的傅里叶变换(周期图法)，也可借助截断信号自相关的傅里叶变换(自相关法)。

傅里叶变换是针对无限区间的，因此这里讨论的信号都是无限延伸的。现实中观测时长有限，记录到的信号严格讲都属于能量信号，但只要持续时间相较于观测时间足够长，通常都会计算功率谱而非能谱。此时不必取极限，直接用信号实际持续时长$T$对能谱约化：

$$S(f) = \frac{1}{T} |X(f)|^2$$

这里其实是将信号视为以$T$为周期的函数(功率信号)，使用单周期数据计算功率(谱)，被称为功率谱的周期图(periodogram)近似。对于平稳随机信号，还可通过对不同时间区间功率谱求平均，缓解随机噪声造成的功率谱波动，具体参见下面DFT部分。而对于非平稳信号，可通过对数据划分时间片段，分别计算功率谱，获得二维的时频谱(spectrogram)，反映出信号在频域随时间的演化。注意这其中对信号的截断会限制频谱分辨率，但分辨率只要能满足实际需求即可。

量纲分析
前面已介绍，所谓“能量”和“功率”都是约定俗称的称呼，并不一定具有能量和功率的量纲，会引起一些困惑，这里展开讨论下。以电压信号为例，取$x(t)$单位为$V$，根据定义：

$$E = \int |x(t)|^2 dt, ~~~ P = \frac{E}{T}$$

在量纲上$[E] = [x]^2[t], [P] = [x]^2$，因此能量单位为$V^2 s$ 或 $V^2 \text{Hz}^{-1}$，功率单位为$V^2$。对于离散谱，表示的是特定具体频率对应的能量或功率，因此单位与能量/功率单位相同。对于谱密度，对应能量/功率分散在连续频率区间，即每$\text{Hz}$的能量/功率，单位要除以$\text{Hz}$，因此能谱密度和功率谱密度单位分别为$V^2 \text{Hz}^{-2}$、$V^2 \text{Hz}^{-1}$。
另一方面，直接根据傅里叶变换：

$$X(f) = \int x(t) e^{-i 2\pi f t} dt$$

在量纲上$[X] = [x][t]$，因此连续谱$X(f)$单位为$V s$ 或 $V \text{Hz}^{-1}$。而根据Parseval定理有$[E] = [x]^2[t] = [X]^2[f]$，在量纲上是一致的。同时能谱密度在量纲上有$[S_E]=[X]^2$，功率谱密度有$[S]=[X]^2[t]^{-1}$，与前面的分析也是一致的。

最终总结起来有：

时域信号 $x(t)$	总能量 $E$	频谱 $X(f)$	功率/离散功率谱 $P, P(f_k)$	能谱密度 $S_E(f)$	功率谱密度 $S(f)$	幅度谱密度 $S_A(f)$
$V$	$V^2 s$	$V~\text{Hz}^{-1}$	$V^2$	$V^2 s~\text{Hz}^{-1}$	$V^2~\text{Hz}^{-1}$	$V/\sqrt{\text{Hz}}$

注1：前面提到，对于各态经历的随机过程，功率在数学上其实对应于随机信号的方差，相应的在量纲上$[P]=[x]^2$，与上面结果是一致的。

注2：这里以电压信号为例，$V$为单位伏特，但其实可将$V$理解为指代任意时序信号单位，代入相应符号即可，如记录位置信息的$m$或速度信息的$ms^{-1}$等。在数学上，时序信号并不需要有明确的单位，甚至可以是无量纲的。比如引力波强度通常用引力波引起的时空应变(strain)幅度表示，由探测器臂长变化比例度量，是无量纲量，其功率谱密度单位为$\text{Hz}^{-1}$。当然自变量也不必是时间，因此其中的$s$或$\text{Hz}$也会根据具体应用而变，比如长度/波数。

注3：工程上绘制功率谱时，一种常见做法是对约化功率取对数，$d_p = 10\log_{10} \frac{p}{p_0}$，单位记为dB(分贝)，在量纲上其实是无量纲的。而约化因子$p_0$通常是1个单位的典型值，比如对功率可取1mW或1W（对应dBm, dBW），从而$p' = 10\log_{10} p$。此外，对于平方对应功率的量(root-power quantity)，分贝值定义为$d_a = 10\log_{10} \frac{a^2}{a_0^2} = 20\log_{10} \frac{a}{a_0}$，因此由幅值计算分贝值，形式上与功率的定义相差2倍，物理意义上保持一致。变换后，离散谱纵轴单位为dB，而谱密度则记为dB/Hz。取对数的好处在于可凸显取值较小部分，也便于直观反映信噪比(除变减)。

注4：这里引入了幅度谱密度(Amplitude Spectral Density, ASD)的概念，被定义为功率谱密度开二次根号$S_A(f) = \sqrt{S(f)}$。注意，这里的幅度谱密度$S_A(f)$与复频谱取模长得到的幅度谱$A(f)$是不同的，两者量纲上不一致。ASD优势在于，对平稳随机信号，其波动幅度(方差)与信号本身的波动幅度是线性正比的，因此也被称为线性谱密度(Linear Spectral Density, LSD)。相对的，PSD对频率区间的积分为对应频带信号的功率，ASD则失去了这种直观意义。

注5：另一个与PSD相关的常见物理量为$fS(f)$，量纲上消去了频率，$\sqrt{f S(f)}$量纲与时域信号一致，物理意义上近似为带宽$f$内总功率。优点在于绘制对数图时，如果仅横轴(频率)取对数，曲线对频率区间积分的功率意义得以保持，$\int S(f)f ~ d\ln f = \int S(f) df$。问题是双对数坐标下该怎么直观理解？

离散序列频谱

DTFT
在介绍离散序列DTFT时，给了两种形式的定义：

$$X_{\frac{1}{T_s}}(f) = \sum_{-\infty}^{\infty} x_n e^{-i 2\pi f ~ nT_s}; ~~~~~ X_{\frac{1}{T_s}}(f) = \sum_{-\infty}^{\infty} x[n] e^{-i 2\pi f ~ nT_s}$$

其中$T_s$为采样间隔，对应DTFT周期为$\frac{1}{T_s}$。$x_n = x(nT_s)$为信号采样，$x[n]$为信号采样与采样间隔的乘积$x_nT_s$，两者相差了因子$T_s$。后一种定义下，频谱在量纲上与前面的讨论一致，前一种则不一致。为方便与DFT直接对应，这里会使用前一定义，但能谱/功率谱在量纲上仍会与前面保持一致。
根据DTFT下Parseval定理：

$$\sum_{n=-\infty}^{\infty} |x_n|^2 = T_s\int_\frac{1}{T_s} \left|X_\frac{1}{T_s}(f)\right|^2 df$$

对应于连续信号“能量”定义，离散序列能量和能谱可定义为($T_s$对应积分中的$dt$)：

$$E = T_s \sum_{n=-\infty}^{\infty} |x_n|^2, ~~~ S(f) = T_s^2\left|X_\frac{1}{T_s}(f)\right|^2$$

在总能量发散时，可基于有限区间$[-N, N]$的离散信号引入功率及功率谱的概念：

$$P = \lim_{N\rightarrow\infty} \frac{1}{(2N+1)T_s} T_s\sum_{n=-N}^{N} |x_n|^2$$

$$S(f) = \lim_{N\rightarrow\infty} \frac{T_s}{2N+1} \left|X_{2N+1}(f)\right|^2 = \lim_{N\rightarrow\infty} \frac{\left|X_{2N+1}(f)\right|^2}{(2N+1)f_s}$$

由于输入进行了截断，其DTFT不再是无限序列的$X_\frac{1}{T_s}(f)$，而是卷积了窗口函数的频率响应，这里记为$X_{2N+1}(f)$，表示是与$[-N, N]$区间序列对应的DTFT。

DTFT到DFT
前面已介绍，时频域之间的离散化与周期性延拓互为对偶，对频谱的采样对应于时域信号折叠延拓。设DTFT频谱$X_{\frac{1}{T_s}}(f)$每个周期采样数为N，记为$X_N[k]$，则：

$$X_N[k] = X_{\frac{1}{T_s}}\left(\frac{k}{NT_s}\right) = \sum_{-\infty}^{\infty} x[n] e^{-i 2\pi \frac{k}{N} n} = \sum_{n=0}^{N-1} x_N[n] e^{-i 2\pi \frac{k}{N} n}$$

其中$x_N[n]=\sum_{m=\text{-}\infty}^{\infty} x_{n~\text{mod}~N}$，对应于$\{x_n\}$以$N$为单位无限平移求和所构造的周期性函数，或者将$\{x_n\}$切分为长度为N的片段折叠求和，并周期性延拓。上式最后的数学形式为DFT，即离散序列DTFT频谱的采样可直接由$x_N[n]$的DFT得到。

下面考虑功率谱的采样，记离散样本总数为L。当L等于N，$x_N[n]$对应于$x_n$的直接延拓，若L小于N，$x_N[n]$对应于$x_n$补零后周期性延拓，此时功率和功率谱采样：

$$P = \frac{1}{L T_s} T_s \sum_{l=0}^{L-1} |x_l|^2 = \frac{1}{L} \sum_{n=0}^{N-1} |x_N[n]|^2, ~~~ S(f_k) = \frac{1}{L f_s} |X_N[k]|^2$$

当L大于N，$x_N[n]$对应于$x_n$折叠求和后的周期性延拓。假设L=MN为N的整数倍，此时可将样本切分为M段，而功率和功率谱采样：

$$P = \frac{1}{L T_s} T_s \sum_{l=0}^{L-1} |x_l|^2 = \frac{1}{MN} \sum_{m=1}^{M} \sum_{n=0}^{N-1} |x_{m,n}|^2 = \frac{1}{M} \sum_{m=1}^{M} \frac{1}{N} \sum_{n=0}^{N-1} |x_{m,n}|^2$$

$$S(f_k) = \frac{1}{M} \sum_{m=1}^{M} \frac{1}{N f_s} |X_{m,k}|^2 = \frac{1}{M} \sum_{m=1}^{M} S^{(m)}(f_k)$$

这里$S^{(m)}(f_k)$为其中一段样本的功率谱，即功率谱采样对应样本分段计算功率谱的平均。注意是正比于各段DFT模方的平均，而非各段DFT平均的模方($|X_{N}[k]|^2$)。

利用DFT频谱计算功率谱，对应于离散样本的周期性延拓，即周期图法(periodogram)。应用时有几个变种：

• 最简单的周期图：直接进行DFT，计算功率谱，对应样本直接延拓
• Bartlett法：数据分段后分别DFT，计算功率谱，最后求平均，对应于样本折叠延拓
  对于随机过程，简单的周期图法得到的功率谱存在较大随机波动，Bartlett法则牺牲了一定频率分辨率，但通过求平均，减少了噪声的干扰。
• Welch法：数据分段时可重叠，DFT前加窗，计算功率谱，最后求平均
  Bartlett法直接切分数据，相当于对数据加了矩形窗，而矩形窗存在较大频谱泄露。Welch法的出发点是通过其它窗口函数，改善频谱泄露。而窗口函数会压低边缘数据，因此作为补偿Welch在数据分段时允许一定程度重叠。
• 非均匀采样：Lomb-Scargle周期图，对数据逐点加权

DFT

$$X_k = \sum_{n=0}^{N-1} x_n e^{-i\frac{2\pi k}{N} n}, k \in [0, N -1]$$

在量纲上，对于DFT，$[X_k] = [x_n]$，频域与时域单位的一致！考虑到DFT对应于时域序列周期性延拓的变换，其功率可对单个周期做平均，根据Parseval定理：

$$\sum_{n=0}^{N-1} |x_n|^2 = \frac{1}{N}\sum_{k=0}^{N-1} |X_k|^2$$

$$P = \frac{1}{NT_s} T_s\sum_{n=0}^{N-1} |x_n|^2 = \frac{1}{N^2}\sum_{k=0}^{N-1} |X_k|^2$$

注意，离散采样的平均功率为$\frac{1}{N}\sum |x_n|^2$而非$\frac{1}{T}\sum |x_n|^2$。此外，这里NT_s是参与傅里叶变换的信号实际长度：DFT计算时会根据指定的nfft对信号补零或截断，这里的N对应于输入序列长度L与nfft中较小者min(L, nftt)。

最终，离散信号基于DFT的功率谱为：

$$\boxed{P(f_k) = \left|\frac{X_k}{N}\right|^2}$$

注意，周期信号对应离散谱，因此这里得到的是离散功率谱而非连续的谱密度。在量纲上$[P(f_k)] = [X_k]^2 = [x]^2$，与前面的量纲分析保持一致。从傅里叶级数角度理解，前面提到，频域分解系数$\alpha_k$对应于$\frac{X_k}{N}$，而$P(f_k)$就是各频率成分幅度占比的平方。

要估算对应的功率谱密度，需要将功率平均到频率区间$\frac{1}{NT_s} = \frac{f_s}{N}$：

$$\boxed{S(f_k) = \frac{P(f_k)}{f_s/N} = \frac{\left|X_k\right|^2 }{f_s N}}$$

形式上与前面DTFT功率谱密度对应，量纲上$[S(f_k)] = [X_k]^2[f]^{-1}$，也与前面的连续信号谱密度一致。从连续的傅里变换角度理解，前面提到，DFT频谱与连续频谱关系为$X_k = \frac{X(f)}{T_s} = X(f)f_s$，而功率谱密度为$\frac{1}{T}|X(f)|^2 = \frac{1}{NT_s}|X(f)|^2 = \frac{1}{Nf_s}|X_k|^2$。

最后作为简单示例，考虑单频正弦信号，其功率等于振幅平方的一半：

$$P_{f_{k}} = \frac{1}{2}A_{f_k}^2 = \sum_{k'=0}^{N-1} \left|\frac{X_{k'}}{N}\right|^2 = 2\left|\frac{X_k}{N}\right|^2 = 2P(f_k), ~~~~ A_{f_k} = 2\left|\frac{X_k}{N}\right|$$

求和时只有正负$f_k$谱值非零，且两者谱值相同，因此总功率为2倍的$P(f_k)$。也正因如此，振幅$A_{f_k}$是幅度谱$A(f_k)=\sqrt{P(f_k)}$的2倍，而非$\sqrt{2}$倍(对单边谱是$\sqrt{2}$倍)。

import numpy as np
A, freq = 0.5, 50
fs, N  = 1000, 2000
times = np.arange(N)/fs
singal = A*np.sin(2*np.pi*freq*times)
mag = np.abs(np.fft.fft(singal))/N

k = int(freq/(fs/N)) # df = fs/N
print(A, 2*mag[k])

单边 v.s. 双边
前面讨论的频谱默认都包含负频率，但对于实信号负频率信息是冗余的，其频谱具有共轭对称性，功率谱具有对称性。考虑到在工程实践上，只有正频率具有实际意义，因此很多时候会忽略负频率部分，仅保留单边谱。此时能谱/功率谱需要乘以2，以保证能量守恒。对于复信号频谱不具有上述对称性，也就没有所谓单边谱。

$$S_\text{+}(f) = \begin{cases} 0 ~&\text{if } f<0\\ S(f) ~& \text{if } f=0\\ 2S(f) ~& \text{if } f>0 \end{cases}$$

傅里叶变换将信号拆解为复信号的叠加$e^{i2\pi f t}$。对于实信号，正频率分量对应有共轭对称的负频率分量，以抵消虚数部分$\frac{e^{i2\pi f t}+e^{-i2\pi f t}}{2} = \mathrm{Re}(e^{i2\pi f t})$。唯一的例外是零频率分量，正负频率重合(对应实信号)，只有一个分量。相应的单边频谱中，零频率无需翻倍。

而在离散变换中$e^{i2\pi f t} = e^{i2\pi \frac{k}{N}f_s nT_s} = e^{i2\pi \frac{k}{N} n}$，除了零频率分量外，Nyquist频率分量为$e^{i\pi n}=\pm 1$，同样是纯实信号(正负频率重合)，也只对应一个分量。因此DFT变换得到的频谱，计算单边谱时，Nyquist频率同样无需翻倍。不过，Nyquist频率只有N为偶数才能取到，因此只有偶数N才需考虑。

if mode == 'psd' and sides == 'onesided':
    if nfft % 2:
        S[1:] *= 2    # skip DC
    else:
        S[1:-1] *= 2  # skip DC + Nyquist
# 这里S只对应区间[0, 1/2f_s]部分频谱，N为偶数时[-1]分量对应Nyquist频率

最后，零频率成分对应信号的时间平均，实际分析时可通过减均值移除DC分量，此外通常会调整采样频率，使Nyquist频率高于关注的信号频段，因此零频率和Nyquist频率的特殊情况影响不大。

窗口修正因子

引入窗口函数后，输入序列由$x'_n$变为$w_n x'_n$，DFT频谱$X_k$对应于$\frac{1}{N} W_k \circledast X'_k$。显然不同窗口函数具体值不同，且不能通过简单的变换由$X_k$得到原输入序列频谱$X'_k$。但考虑到窗口函数频率响应是位于零频率附近的尖峰，近似可取$X_k = \frac{W_0}{N} X'_k$，从而$X'_k = \frac{N}{W_0} X_k$，其中$W_0$为窗函数频谱位于零频率处的峰值。据此，对于离散功率谱有：

$$P(f_k)=\left|\frac{X'_k}{N}\right|^2 = \left|\frac{X_k}{W_0}\right|^2$$

为了进一步对功率谱密度进行修正，则需要引入“等效噪声带宽”的概念。

等效噪声带宽ENBW(Equivalent Noise BandWidth)

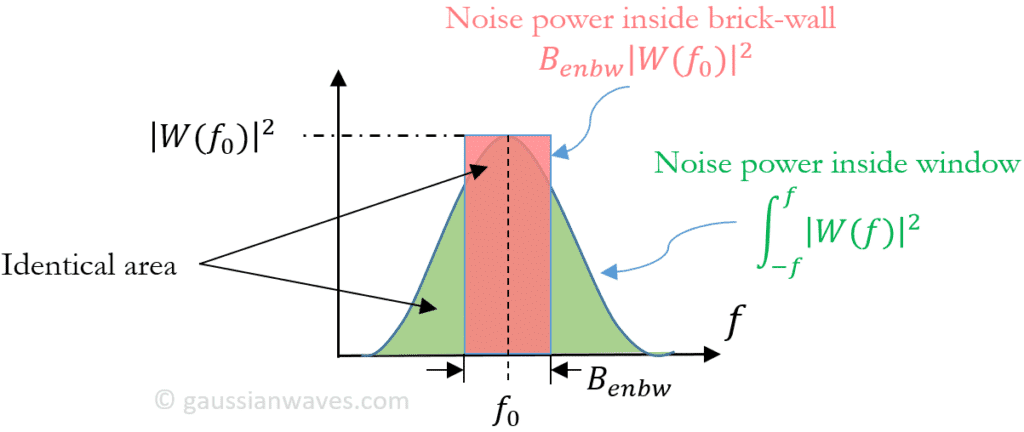
等效噪声宽度ENBW为窗口频率泄露功率所对应的等效频率区间宽度，随机噪声信号在不同窗口函数下的噪声水平就正比于等效噪声宽度。具体的，其定义为窗口函数总功率与功率密度谱峰值的比值，或者总能量与能谱密度峰值的比值。

$$\text{ENBW} \equiv \frac{E_{\rm window}}{S_E(f_0)} = \frac{\displaystyle\int |w(t)|^2 dt}{|W(f_0)|^2} = \frac{\displaystyle\int |W(f)|^2 df}{|W(f_0)|^2}$$

对于离散窗口，利用DTFT同样有：

$$\text{ENBW} =\frac{T_s \sum |w_n|^2}{ T_s^2 |W(f_0)|^2} = f_s\frac{\sum |w_n|^2}{|W(f_0)|^2} = \frac{\displaystyle\int_{f_0-\frac{f_s}{2}}^{f_0+\frac{f_s}{2}} |W(f)|^2 df}{|W(f_0)|^2}$$

这里$f_0$为中心频率，基带情况下对应零频率。对零频率分量有$W_0=\sum w_n$，从而：

$$\boxed{\text{ENBW} = f_s\frac{\sum |w_n|^2}{|\sum w_n|^2} }$$

由于采样频率$f_s$的存在，ENBW并不完全由窗口本身决定。考虑到DFT的频谱分辨率(区间宽度)为$\frac{f_s}{N}$，通常会约化采样频率，使用等效的频率区间数(bins)来描述窗口函数：

$$\boxed{ \text{ENBW}_\text{bin} = \frac{1}{f_s/N}\text{ENBW} = N \frac{\sum |w_n|^2}{|\sum w_n|^2}}$$

$\text{ENBW}_\text{bin}$ 完全由窗口函数决定，是其核心指标之一，且矩形窗取值刚好为1。

最终信号功率谱(密度)的修正为：

• 功率谱

  $$P(f_k) = \left|\frac{X_k}{W_0}\right|^2 = \left|\frac{X_k}{\sum w_n}\right|^2$$

  对应于矩形窗下有$P(f_k) = \left|\frac{X_k}{N}\right|^2$，与之前结果一致。
• 功率谱密度

  $$S(f_k) = \frac{P(f_k)}{\text{ENBW}} = \frac{|X_k|^2}{f_s \sum |w_n|^2}$$

  对应于矩形窗下有$S(f_k) = \frac{P(f_k)}{f_s/N} = \frac{|X_k|^2}{f_s N}$，与之前结果一致。

最后，相对矩形窗情况，引入窗函数后的修正因子，功率谱为窗函数均值的平方 $(\sum w_n / N)^2$，谱密度为窗函数均方根的平方$\sum |w_n|^2 / N$。

if scaling == 'spectrum':
    scale = 1.0 / win.sum()**2
elif scaling == 'density':
    scale = 1.0 / (win**2).sum() / fs
#if mode == 'stft':
#    scale = np.sqrt(scale)

Python实现

• Numpy：abs, angle, unwrap [fft]fft, fftshift, fftfreq, rfft, rfftfreq
• Scipy：[fft] fft, fftshift, fftfreq, rfft, rfftfreq
  　　　[signal] welch, csd, periodogram, lombscargle; spectrogram, stft
• Matplotlib：[pyplot]psd, csd, magnitude|angle|phase_spectrum; specgram

傅里叶变换

• fft(x, n=None)：n点FFT，根据n对输入补零或截断，默认等于输入序列长度
• fftfreq(n, d=1.0)：基带频率，时域采样间隔d默认为1，对应归一化的频率
• fftshift(arr)：序列前后两半对调，一维序列即np.roll(arr, len(arr)//2)
• np.abs(x)、np.angle(x)可由fft计算的复频谱获取幅值谱(模)和相位谱(幅角)
• rfft(x, n=None), rfftfreq(n, d=1.0)可获取实信号的单边复谱及对应基带频率

fft返回的频谱序列对应频率$\frac{k}{N}f_s$，频率区间$[0, f_s)$，对应基带$[0, \frac{1}{2}f_s) \cup [-\frac{1}{2}f_s, 0)$。fftfreq(n)可给出对应的基带频率，[0]为零频率，[1:N//2]为正频率，[N//2:]为负频率。而fftshift(arr)则将序列后半部分调换至序列最前面，fft频谱和fftfreq频率要同时shift，以保持对应，最终频谱序列对应频率区间$[-\frac{1}{2}f_s, \frac{1}{2}f_s)$。

Nyquist频率只有N为偶数时才能取到，因此奇数N实际对应区间$(-\frac{1}{2}f_s, \frac{1}{2}f_s)$。在N为偶数时，fft频谱[N//2]分量对应Nyquist频率，fftfreq将其值设为$-\frac{1}{2}f_s$，而fftshift将其平移至序列首位。

FFT算法的效率在N为2的指数时最高，因此通常会将n取为256, 512等2的指数。当输入信号为实数可只计算[0:N//2+1]部分，利用频谱共轭对称性获取后半部分，计算时fft会根据输入自动切换至该算法。

功率谱

• 功率谱 welch, csd, periodogram
• 时频谱 spectrogram, stft
• 其他：非均匀采样(lombscargle)、绘图(psd, csd, specgram)

在实现上，功率谱是直接FFT或分段FFT计算功率谱后取平均，时频谱则是分段FFT计算频谱或功率谱，计算时都借助内部函数_spectral_helper。具体的：

• peridogram是仅计算单段数据的welch，welch是x,y相等的csd，
  periodogram不做分段平均，仅考虑 min(nfft, 序列长度) 对应的信号；
• stft计算复值谱(密度)，默认返回离散谱(scaling=‘spectrum’)；
• spectrogram/specgram可返回PSD(默认)、复谱以及幅值、幅角、相位等；
• plt.psd对应signal.welch，plt.specgram对应signal.spectrogram

参数默认值：

• DFT计算长度nfft/pad_to：periodogram为输入序列长度，其余为nperseg
• 序列切片长度nperseg：窗口长度 或 min(256, 序列长度)
• 窗口window：periodogram为矩形框’boxcar’，spectrogram为’tukey’，其余为’hann’
• 重叠noverlap：spectrogram为nperseg//8，其余nperseg//2 (periodogram仅单片段)
• 修正scaling：stft为离散谱(‘spectrum’)，其余均为密度谱(‘density’, scale_by_freq)
• 趋势移除detrend：stft不处理(False)，其余均为扣除均值(‘constant’)
• 单双边谱：默认都为单边谱return_onesided=True/sides='onesided'(只对实信号有效)
• 绘图函数默认window为’hann’(对称窗口)，noverlap为0，detrend为False

值得注意的，nperseg为实际数据(切片)长度，决定了窗口长度及相关的修正因子；nfft为计算FFT的点数，决定了具体的频率值，只有大于数据(切片)长度才有效，小于数据长度时会报错。Matplotlib函数的NFFT参数对应于Scipy的nperseg，pad_to对应后者的nfft，不过目前实现的中存在Bug。

	Matplotlib.pyplot (psd/csd; specgram)	Scipy.signal (periodogram/welch/csd; spectrogram/stft)	特殊
window	'hann’对称窗口	'hann’周期性窗口	signal.periodogram为’boxcar’， signal.spectrogram为’tukey’
noverlap	0	nperseg//2	plt.specgram为128， signal.periodogram为0， signal.spectrogram为nperseg//8
detrend	None	‘constant’	signal.stft为False
Fs, fs	2	1

注意：

1. 对于实信号，默认都是单边谱，而返回双边谱时，Matplotlib对应fftshift平移后顺序，Scipy则是未平移结果。
2. Matplotlib函数返回值为正常谱值，但绘图时会自动将谱值变换为分贝值，功率谱对应$10\log_{10}(p)$，幅度谱对应$20\log_{10}(a)$。

# plt.psd  v.s. signal.welch
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt

rng = np.random.default_rng(42)
fs = 1000
f = 100
t = np.arange(0, 1, 1/fs)
s = np.sin(2 * np.pi * f * t) + 0.5 * rng.normal(size=t.shape)

nfft = 512
# NFFT → nperseg
fig, axes = plt.subplots(2, 1, sharex=True)
psd, freqs = axes[0].psd(s, NFFT=512, Fs=fs)
freqs1, psd1 = signal.welch(s, nperseg=512, fs=fs)
axes[0].plot(freqs1, 10*np.log10(psd1))
relative_error = np.abs( 2 * (psd-psd1)/(psd + psd1) )
axes[1].plot(freqs, relative_error)
axes[1].set_ylabel('relative error')
plt.show()

# detrend=False, noverlap=0
fig, axes = plt.subplots(2, 1, sharex=True)
psd, freqs = axes[0].psd(s, NFFT=512, Fs=fs)
freqs1, psd1 = signal.welch(s, nperseg=512, fs=fs,
                            detrend=False, noverlap=0)
axes[0].plot(freqs1, 10*np.log10(psd1))
relative_error = np.abs( 2 * (psd-psd1)/(psd + psd1) )
axes[1].plot(freqs, relative_error)
axes[1].set_ylabel('relative error')
plt.show()

# window: periodic v.s. symmetric
win = signal.windows.hann(512)  # symmetric
# win = signal.get_window('hann', 512) # periodic
fig, axes = plt.subplots(2, 1, sharex=True)
psd, freqs = axes[0].psd(s, NFFT=512, Fs=fs)
freqs1, psd1 = signal.welch(s, nperseg=512, fs=fs,
                            detrend=False, noverlap=0,
                            window=win)
axes[0].plot(freqs1, 10*np.log10(psd1))
relative_error = np.abs( 2 * (psd-psd1)/(psd + psd1) )
axes[1].plot(freqs, relative_error)
axes[1].set_ylabel('relative error')
plt.show()

# twoside + fftshift
fig, axes = plt.subplots(2, 1, sharex=True)
psd, freqs = axes[0].psd(s, NFFT=512, Fs=fs, sides='twosided')
freqs1, psd1 = signal.welch(s, nperseg=512, fs=fs,
                            detrend=False, noverlap=0,
                            return_onesided=False, window=win)
axes[0].plot(freqs1, 10*np.log10(psd1))
psd1 = np.fft.fftshift(psd1)
relative_error = np.abs( 2 * (psd-psd1)/(psd + psd1) )
axes[1].plot(freqs, relative_error)
axes[1].set_ylabel('relative error')
plt.show()

调制
作为信息传输载体的载波信号(carrier)，具有明确的频率和幅度的单频信号，作为实际信息的调制信号(modulation)则通常是具有一定带宽的信号。载波通常比输入信号具有更高的频率，用于实现信息的传递，通过不同的载波信号可将信息分散在不同频段，共用相同的传输媒介(频分复用)。经过调制的信号频谱则表现为位于中心的载波频率，以及左右两侧的边带(对应实际信息)。

最简单的例子，假设载波信号为$c(t) = A_0 \cos(\omega_0 t + \phi_0)$

• 调幅AM：$A = s(t)A_0$， $x(t) = s(t)A_0 ~ \cos(\omega_0 t + \phi_0) = s(t)c(t)$
• 调频FM：$\omega = \omega_0 + 2\pi f_{\Delta}s(t)$，$x(t) = A_0\cos\left(\omega_0t + 2\pi f_{\Delta}\int_0^t s(\tau)d\tau + \phi_0\right)$
• 调相PM：$\phi = \phi_0 + s(t)$， $x(t) = A_0\cos\big(\omega_0t + s(t) + \phi_0 \big)$

卷积相关 Conv & Corr

卷积与相关

$$(f \star g)(\tau) = \int_{-\infty}^{\infty} \overline{f(t)}~g(t+\tau)dt ~~~~~ \text{v.s.} ~~~~~ (f * g)(\tau) = \int_{-\infty}^{\infty} f(t)~g(\tau-t)dt$$

互相关的定义式是希尔伯特空间中的函数内积，取共轭是内积所必须的，也保证了函数与自身内积为正实数。据此，相关可视为两个无限长向量的“滑动点积”，而点积反映了向量相似度。因此相关的直观意义很明确，就是度量两个序列(函数)在不同位移量下的相似度，可用于序列的特征检测：比如通过与已知信号互相关检测序列中的特定模式，又或者通过序列的自相关揭示内在周期性。

卷积与相关核心区别在于在“滑动点积”前多了反转操作(同时也无需取共轭)。可视作$f(t)$的加权累积，权重为$g(-t)$，而随着$g(-t)$的平移得到了一个函数。为理解其直观意义，一个角度是将其视为输入信号的累积影响，将$f(t)$作为单位时间的输入，$g(t)$作为零点“单位瞬时脉冲”输入的持续影响(随时间演化)，这里假设输入的影响是线性可加的。时刻$\tau$受到$t$时刻输入$f(t)dt$的影响为$f(t)g(\tau-t)dt$，或者说，时刻$\tau$受到$t$时刻之前输入$f(\tau-t)dt$的影响为$f(\tau-t)g(t)dt$。所有时刻输入在时刻$\tau$的总影响可直接累加：

$$\int_{-\infty}^{\tau} f(t)g(\tau-t) dt = \int_{0}^{\infty} f(\tau-t)g(t) dt$$

假设$g(t)=0, t<0$，上述积分等价于：

$$\int_{-\infty}^{\infty} f(t)g(\tau-t) dt = \int_{-\infty}^{\infty} f(\tau-t)g(t) dt$$

这就是卷积$f(t) * g(t)$。一般地，若不限制$g(t)=0, t<0$则意味着当前时刻之后的输入也会对当前时刻产生影响，虽然不符合因果律的限制，但在数学形式上具有一般性，尤其是当自变量$t$不是时间时，如对空间函数的卷积，并不需要考虑因果律的限制。

具体的，以背单词为例，假设时间$dt$内新学习词汇数量为$f(t)dt$，而词汇量衰减的遗忘曲线为$g(t)$。任意时刻$\tau$，时刻$t$所学词汇$f(t)dt$剩余量为$f(t)g(\tau-t)dt$，总词汇量为之前所学习词汇在经历遗忘衰减后的累积$\int_{-\infty}^{\tau} f(t)g(\tau-t)dt$。这里$g(t)$是随时间衰减的，如果以复利为例，则$g(t)$将是随时间增长的。

除了上述“输入影响的持续累积”，卷积还有其它很多不同视角：

• 若将$g(t)$作为归一化的窗口函数，则卷积就是统计中加权的滑动平均。
• 在概率论中，假设独立随机变量$\mathbf{x}, \mathbf{y}$分布函数分别为$f(t), g(t)$，则$\mathbf{x+y}$的概率密度是各自分布的卷积$f*g$，$\mathbf{y-x}$的概率密度是各自分布的互相关$f\star g$。
• 与上述结论密切相关的一个视角是，设平面坐标系$(t_1, t_2)$对应值为乘积$f(t_1)g(t_2)$，沿-45°对角方向卷起整个平面(积分)得到的一维函数就是卷积($t_1=\tau-t_2$)，而沿45°对角方向卷起整个平面(积分)得到的一维函数就是相关($t_1=\tau+t_2$)。
• 利用卷积定理，$\mathcal{F}\{f * g\} = \mathcal{F}\{f\}\mathcal{F}\{g\}$，从频域理解，卷积是滤波操作，后面滤波器部分具体介绍。在图像处理卷积可实现图像的平滑或锐化，低通滤波对应对输入的平滑，高通滤波则对应对输入的锐化。
• 对于信号处理系统，$f(t)$作为输入，$g(t)$对应于系统的单位脉冲响应，而卷积操作则对应于线性时不变LTI系统对信号的作用，后面线性系统中会具体介绍。
• 根据微分性质，$(f * g)' = f' * g = f * g'$，$f*g$可导仅要求$f$与$g$其中之一可导，总的可导阶数为f与g阶数之和，从这个角度$f*g$要比$f, g$都更光滑。假设$f$为任意数据，$g$为平滑函数，如高斯函数，$f * g$是对$f$进行平滑，而其导数可用于近似$f$本身的导数，计算时只需要$f*g'$即可，利用这点可更好地计算数据的导数，类似的可计算任意高阶导数。这就是图像处理中高斯拉普拉斯LoG(Laplacian of Gaussian)算子的来源。

• 对于对称实信号，或一般的哈密顿函数$\overline{f(t)} = f(-t)$，卷积与互相关一致，可从函数内积角度理解。注意互相关不具有交换率，若$f$对称，则$f*g = g*f = f\star g$，若$g$对称，则$f*g = g*f = g\star f$。

卷积在实践中很常见，不同应用下的具体意义关联性可能不大，可在具体应用场景中去理解，不必强求统一的直观理解。事实上，任何数据测量过程都可理解为测量系统对于实际信号的响应。而如果系统响应是线性的，测量结果就对应于信号与系统响应函数的卷积。考虑到观测精度的限制，卷积将在数据中引入测量误差，需要在后续处理中通过滤波等手段提升信噪比。以天文观测为例，地面观测会受到大气湍流的干扰，观测到的天体亮度分布就是实际亮度与大气视宁度的卷积；而空间观测同样会受到镜片衍射极限的限制，观测到的亮度是实际亮度与望远镜衍射图样的卷积。

• 互相关不满足交换律(以及结合律)$f \star g \neq g \star f$，在频域$\mathcal{F}\{f \star g\} = \overline{\mathcal{F}\{g \star f\}}$
• $f(t) * g(t) = \overline{f(-t)} \star g(t), ~~~ f(t) \star g(t) = \overline{f(-t)} * g(t)$
• $f \star (g * h) = (f \star g) * h$
• 卷积性质
  • 交换律 $f * g = g * f$
  • 结合律 $f * (g * h) = (f * g) * h$
  • 分配律 $f * (g + h)= f * g + f * h$
  • 单位元 $f * \delta = \delta * f = f$
  • 时移 $f(t + a) * g(t + b) = (f*g)(t + a + b)$
  • 缩放 $f(at) * g(at) = \frac{1}{|a|}(f*g)(at)$
  • 微分 $(f * g)' = f' * g = f * g'$
  • 积分 $\int f*g dt = [\int f(t) dt][\int g(t) dt]$
  • 卷积定理 $\mathcal{F}\{f * g\} = \mathcal{F}\{f\}\mathcal{F}\{g\}, ~~~ \mathcal{F}\{f g\} = \mathcal{F}\{f\}*\mathcal{F}\{g\}$
  • 高斯函数的卷积仍是高斯函数，$\mathcal{N}(\mu_1, \sigma_1), \mathcal{N}(\mu_2, \sigma_2)$的高斯函数卷积服从分布$\mathcal{N}(\mu_1+\mu_2, \sqrt{\sigma_1^2+\sigma_2^2})$

相关与功率谱

$$r_{xx}(\tau ) = x(t) \star x(t) = \int_{-\infty}^{\infty} \overline{x(t)}~x(t+\tau)dt$$

上述定义仅对能量信号有意义(积分收敛)，对于功率信号自相关定义为：

$$r_{xx}(\tau )= \lim _{T\rightarrow \infty }{\frac {x_T(t) \star x_T(t)}{T}} = \lim _{T\rightarrow \infty } \frac{1}{T} \int_{-T/2}^{T/2} \overline{x(t)}x(t+\tau ) ~ dt$$

自相关反映了序列在不同位移量下的相似度，为实对称函数，且零点值最大$r(\tau) \le r(0)$，事实上只有周期函数能取到等于号。当自相关函数$r_{xx}$本身为能量信号，其傅里叶变换存在，对应于信号的功率谱，前面功率谱部分已介绍。自相关函数更常用于分析随机过程，具体可参考信号分析II：随机过程。

类似于自相关与功率谱，可定义功率信号的互相关及对应的互功率谱：

$$r_{xy}(\tau )= \lim _{T\rightarrow \infty }{\frac {x_T(t) \star y_T(t)}{T}} = \lim _{T\rightarrow \infty } \frac{1}{T} \int_{-T/2}^{T/2} \overline{x(t)}y(t+\tau ) ~ dt$$

$$S_{xy}(f) = \mathcal{F}\{ r_{xy}(\tau)\} = \int r_{xy}(\tau) e^{-i2\pi f \tau} d\tau$$

需要注意，由于相关不具有对称性，因此$r_{xy}$与$r_{yx}$，及对应的$S_{xy}(f)$与$S_{yx}(f)$并不相同。

需要注意的，这里讨论的相关不同于概率论中的“相关”，后者通常指随机变量的(皮尔逊)相关系数$\rho(X,Y) = \frac{\mathrm{cov}(X, Y)}{\sigma_X \sigma_Y}$，而这里是确定性信号间的相关函数，不存在方差或协方差概念。不过相关函数可推广至随机信号或随机过程，此时可引入作为时间函数的皮尔逊相关系数，对于广义平稳过程有$\rho_{X,Y}(\tau) = \frac{\mathrm{cov}_{X, Y}(\tau)}{\sigma_X \sigma_Y}$，具体可参考信号分析II：随机过程。

离散实现

$$(x\star y)[k] = \sum _{n=-\infty}^{\infty}\overline{x[n]}y[n+k] ~~~ \text{v.s.} ~~~ (x*y)[k] = \sum _{n=-\infty}^{\infty}x[n]y[k-n]$$

对于有限长度的序列，取$x, y$序列长度分别为$N, M$则有：

$$\begin{aligned} (x\star y)[k] =& \sum _{n=0}^{N-1}\overline{x[n]}y[n+k], k \in [-(N-1), M-1] \\ (x*y)[k] =& \sum _{n=0}^{N-1}x[n]y[k-n], k \in [0, N+M-2] \end{aligned}$$

计算时，当指标超出序列$y$范围时对应取0，实现时通常是对序列补零延拓。对于互相关，$k$会取负值，作为索引(非负)可简单平移$k'= k+(N-1)$。定义$y_\text{ext}$为序列$y$前后各补$N-1$个0，则对于互相关有：

$$z[k] = (x\star y_\text{ext})[k] = \sum _{n=0}^{N-1}\overline{x[n]}y_\text{ext}[n+k], k \in [0, N+M-2]$$

而卷积同样可变换为相关：

$$(x*y)[k] = (\overline{x}_\text{invert}\star y_\text{ext})[k], k \in [0, N+M-2]$$

import numpy as np
def xcorr(x, y):
    N, M = len(x), len(y)
    dtype = 'float'
    if np.iscomplexobj(x) or np.iscomplexobj(y):
        dtype='complex'

    zero_ext = np.zeros(N-1)
    y_ext = np.r_[zero_ext, y, zero_ext]
    z = np.zeros(M+N-1, dtype=dtype)
    for k in range(M+N-1):
        z[k] = np.sum(np.conj(x) * y_ext[k:k+N])
    return z

def conv(x, y):
    return xcorr(np.conj(x[::-1]), y)

Python中相关和卷积的基本实现有：

• Numpy：correlate, convolve
• Scipy：[signal] correlate, convolve
• Matplotlib：acorr, xcorr

需要注意的是，在上述实现中互相关(correlate)的定义为$\sum _{m} x_{m+k} \overline{y_{m}}$，等于$(y\star x)[k]$，即对应上面定义中$x, y$对调。而卷积(convolve)由于具有对称性，并没有区别。

from scipy import signal 
x = [1, 2+1j, 3]
y = [0, 1, 2, 3-1j, 4]
print(xcorr(y, x), '\n', np.correlate(x, y, 'full'),'\n', signal.correlate(x, y))
print(conv(y, x), '\n', np.convolve(x, y), '\n', signal.convolve(x, y))

相关和卷积计算时有三种模式：‘full’、‘valid’和’same’：

• 'full’是最常见，计算所有存在重叠的情况，最终输出序列长度为N+M-1，循环卷积的单个周期就回归了普通卷积。因此，对于离散信号只要适当补零，即可；
• 'valid’只计算序列完全重叠的部分，输出序列长度为max(M, N) - min(M, N) + 1，这种模式下无需补零，对于相同长度序列结果只有一个值；
• 'same’介于full与valid之间，Numpy中定义为输出长度等于较长序列max(M, N)，而在Scipy中则是与前一序列长度相同。默认情况下，除了Numpy卷积为’valid’模式，其余均为’full’模式。

上述相关和卷积操作，超出序列范围时取值默认为0，被称为线性卷积。另一种做法是对序列进行周期性延拓，对应单个周期内的结果被称为循环卷积，这样定义的好处是服从DFT变换下的卷积定理。而通过简单的补零延拓，循环卷积可回归至线性卷积，最终可通过FFT计算线性卷积。事实上，在上述实现中，序列较长时会自动切换至基于FFT的算法。

周期卷积与循环卷积
周期相同的两个函数在单个周期内的卷积被称为周期性卷积(periodic convolution)：

$$\int_{t_0}^{t_0 + T} f_T(\tau) g_T(t-\tau) d\tau = \int_{0}^{T} f_T(\tau) g_T(t-\tau) d\tau$$

而有限区间非零的函数通过周期性延拓可得到周期性函数，进而计算周期性卷积，被称为延拓前函数的循环卷积：设周期$T$长于$f(t), g(t)$非零区间长度，$f_T(t) \equiv f \bigl( t~\text{mod}~T \bigr)$为$f(t)$的周期性延拓，$f, g$的循环卷积为$f_T, g_T$的周期卷积：

$$f \circledast g = \int_{t_0}^{t_0+T} f_T(\tau) g_T(t-\tau) d\tau = \int_{-\infty}^{\infty} f(\tau) g_T(t-\tau) d\tau = f*g_T$$

离散形式有(取周期性延拓区间长度为$L$)：

$$x \circledast y = \sum_{l=0}^{L-1} x[l]~y_L[n-l] = \sum_{l=0}^{L-1} x_{\tiny l}~y_{_{(n-l)~\text{mod}~L}}$$

(线性)卷积 v.s. 循环卷积：设序列 $x, y$ 长度分别为N、M，线性卷积 $x \ast y = \sum_l x_{\tiny l}~y_{_{n-l}}$ 在 N+M-1 长度区间内非0，而循环卷积 $x \circledast y = \sum_{l=0}^{L-1} x_{\tiny l}~y_{_{(n-l)~\text{mod}~L}}$ 为周期 L 的序列。引入循环卷积是因其可借助DFT/FFT快速计算，且当L>=N+M-1，循环卷积的单个周期就回归了普通卷积。因此，对于离散信号只要适当补零，即可利用FFT快速计算卷积。

线性滤波

滤波器或过滤器(filter)是用于移除或抑制输入信号部分成分、提取或凸显目标成分的算法或模块。如耳机的降噪、图片的抠像，又或者去除时序信号中的周期性波动、线性偏置等。从不同角度可分为线性与非线性、时变与时不变、因果与非因果等。这里简单解释下因果性，以时列信号处理为例，常见的应用场景有：

• 过滤：利用当前及之前含噪声的观测数据，估计当前信号值
• 预测：利用当前及之前含噪声的观测数据，估计未来信号值
• 平滑：利用过去及未来含噪声的观测数据，估计当前信号值

这其中，前两者处理时只利用过往及当前数据，符合因果律限制，为因果滤波，最后一种情况利用了未来数据，属于非因果滤波。显然对于时序信号，因果滤波可实时运行，而非因果滤波不行。

下面主要关注最简单的线性时不变滤波器。对于线性时不变系统，其作用可通过“卷积”描述$y(t) = h(t) * x(t)$，其中$h(t)$为系统的脉冲响应函数，具体可参考下面线性系统部分对这类系统的一般性介绍。基于卷积定理，时域卷积等于频域相乘：

$$Y(f) = H(f)X(f)$$

其中$H(f)$为脉冲响应$h(t)$的傅里叶变换，被称为系统的频率响应(frequency response)。对上式取模，$|H(f)|$其实反映了不同频率成分在经过系统后，振幅被增强或减弱的程度，被称为系统对不同频率输入的“增益”。基于对不同频率成分的增益可对滤波进行划分：

• 低通(highpass)滤波：仅低频成分通过，低频增益为1，高频为0(或接近0)
• 高通(lowpass)滤波：仅高频成分通过，高频增益为1，低频为0
• 带通(bandpass)滤波：仅特定频带通过，特定频带增益为1，其余为0
• 带阻(bandstop)滤波：特定频带不通过，特定频带增益为0，其余为1
• 全通(allpass)滤波：所有频带增益都为1，常用于调整信号的相位

注意，虽然对于线性时不变的滤波系统，基于卷积定理，频域角度的理解和计算都很直观。但频域视角并非必要的，有时候也并不比时域/空域更直观，比如图片的抠像。

下面通过高斯函数来直观理解低通和高通滤波的时域效果。高斯函数FT为其自身，以$e^{-\pi f^2}$作为低通滤波的频响函数，在时域对应于$e^{-\pi x^2}$，与时域信号卷积对应于数据的移动平均。相对的，$1-e^{-\pi f^2}$可作为高通滤波的频响函数，在时域对应于$\delta(x) - e^{-\pi x^2}$，中间为正、两侧为负数，与时域信号卷积时对应于数据的差分操作。即时域的平均滤波为低通滤波，抹平高频波动；时域的差分滤波为高通滤波，抑制低频趋势，以线性偏置为例，$y_n = a n$，简单差分有$y_n-y_{n-1} = a$，消除了整体的偏置，凸显小尺度波动。

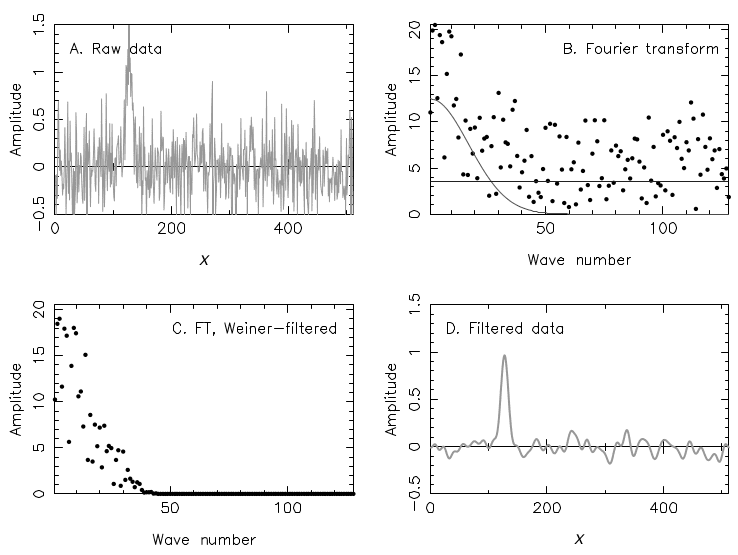
在具体应用上，现实观测数据总是存在随机噪声，假设噪声为白噪声，则其频谱为常数，覆盖所有频段，如果信号集中在低频，就可以通过忽略高频部分，降低噪声的占比。对广义平稳过程，基于均方误差最小可得到(维纳滤波)：

$$H(f) = \frac{S_s(f)}{S(f)} = \frac{S_s(f)}{S_s(f) + S_n(f)}$$

这里假设观测数据为信号+零均值噪声，两者广义平稳且相互独立。$S(f), S_s(f), S_n(f)$分别为数据、信号及噪声的功率谱，这里利用了不相关(零均值)平稳过程功率谱的可加性，下图展示了上述低通滤波的效果。

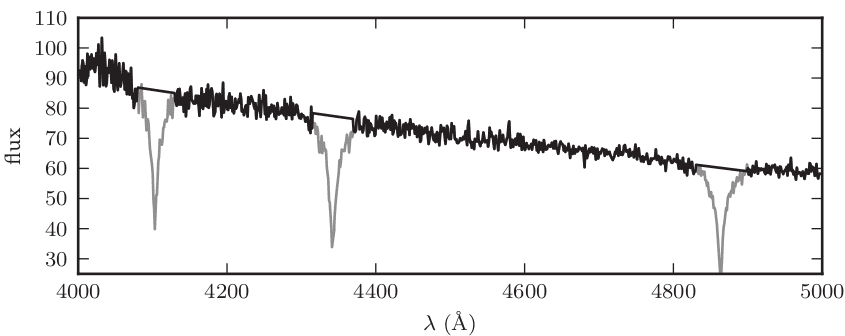
此外，很多时间序列会呈现出整体性的趋势，如线性偏置或缓慢波动，对应于低频信号，因此这种整体趋势的移除(detrend)属于高通滤波。如下图所示的光谱，由整体倾斜的连续谱(基线)和几个吸收谱线组成。考虑到吸收峰的类高斯形状，其功率也集中在低频，因此简单的频域窗口函数并不可行。通常的做法是忽略(mask)吸收峰部分，用线性或低阶多项式拟合剩余部分(黑色)，最后扣除拟合基线，即可保留信号峰，实现高通滤波。此外，也可以对基线和信号峰一起进行参数估计，如MCMC等采样算法。

需要强调的是，虽然滤波可实现数据的降噪或信噪比提升，但数据中的信息通常是有损失的。因此对数据建模，进行参数估计时应该用原始数据(raw data)。

最后，简单介绍其他常见线性时不变滤波，这部分涉及随机过程，只做列举主要结论，具体参考信号分析II：随机过程。

• 白化滤波(Whitening Filter)：指定输入变为(零均值)白噪声

  $$|H(f)| = \frac{1}{\sqrt{S_{xx}(f)}}$$

  这里$S_{xx}(f)$为输入信号的功率谱，输出的白噪声功率谱为常数，对零均值噪声就等于噪声信号随机波动的方差$\sigma^2$，这里取为1。
• 成形滤波(Shaping Filter)：(零均值)白噪声变为指定输出

  $$|H(f)| = \sqrt{S_{xx}(f)}$$

  这里$S_{xx}(f)$为输出信号的功率谱，输入白噪声功率谱取为1。基于成形滤波，可将系统中的有色噪声替换为白噪声输入，只需要将成形滤波作为系统建模的一部分。
• 最优滤波：从噪声数据中重建预期的目标信号(抑制噪声)

  $$\mathbf{x}(t) = s(t) + \mathbf{n}(t), ~~~ \mathbf{y}(t)=\mathbf{x}(t)*h(t)$$

  这里$\mathbf{x}(t)$为观测数据，$s(t)$为其中所包含的信号，$\mathbf{n}(t)$为随机噪声，通常假设为零均值的高斯噪声(不一定是白噪声)。
  • 最小化MSE：使输出$\mathbf{y}(t)$与信号预期$s(t)$的均方误差最小
    维纳滤波(Wiener Filter)、卡尔曼滤波(Kalman Filter)

    $$\displaystyle H(f) = \frac{S_{sx}(f)}{S_{x}(f)}$$

    $H(f)$为维纳滤波频响函数，其中$S_{x}(f), S_{sx}(f)$为输入自相关及输入和预期信号互相关的傅里叶变换，即对应的功率谱/互功率谱。维纳滤波基于频域分析，需要获取信号的自相关、互相关，以计算功率谱，随机过程被限制为广义平稳的。卡尔曼滤波则是基于时域分析（状态空间表示），适用于非平稳过程。两者都是最小均方误差意义下的最佳线性滤波，对于广义平稳过程，两者本质是相同，结果相同。
  • 最大化SNR：使输出$\mathbf{y}(t)$的信噪比最大
    匹配滤波(Matched Filter)

    $$H(f) = k \frac{\overline{X_s(f)}}{S_n(f)}$$

    $S_n(f)$为噪声功率谱，$k$为非零常数。
    对白噪声有$H(f) = k \overline{X_s(f)}$，$h(t) = k s(-t)$，时域响应对应目标信号的反转(相匹配)，因此被称为“匹配”滤波。考虑到反转操作，与$h(t)$卷积等价于与$s(t)$相关，最终匹配滤波就是模板与数据相关，实现信号检测。
    在信号噪声非白噪声时，匹配滤波等价于将数据$x(t)$和模板$s(t)$各自用噪声功率谱$S_n(f)$进行白化后，再进行相关操作：

    $$Y(f) = \frac{ k \overline{X_s(f)}}{\sqrt{S_n(f)}} \frac{X(f)}{\sqrt{S_n(f)}} = \frac{ k \overline{X_s(f)}}{S_n(f)} X(f)$$

    从频域理解，相比数据与模板直接相关，匹配滤波在计算相关时用噪声功率谱倒数进行加权，提升了低噪声频段的权重，进而可提升整体的信噪比。对于平稳的加性(高斯)噪声，匹配滤波是信噪比最大化的线性滤波器，但对于非线性滤波，通过结合信号过程的先验模型可能会取得更好的结果。

品质因子
对于带通滤波，有品质因子(Q-factor)的概念$Q \equiv f_r/\Delta f$。品质因子的定义最初源于谐振子，并可用于更一般的线性时不变系统，用于描述系统脉冲响应的震荡衰减(Damping)，近似正比于系统能量与单次震荡的能量损失之比。对于谐振子而言，$f_r$为响应(共振)的中心频率，$\Delta f$为共振功率谱的半高全宽。对于滤波而言，$f_r$为滤波的中心频率，$\Delta f$为滤波的带宽。对于线性时不变的滤波系统$Y(f)=H(f)X(f)$，其频域响应可理解为频域的窗口函数，理想的滤波对应直接截断的矩形窗，此时带宽可简单定义为增益非零的频率区间长度。但考虑到矩形窗与Sinc互为傅里叶变换，即频域的硬截断在时域会表现出震荡，因此实际实践中滤波通常是渐变衰减，而非理想滤波，此时带宽有多种定义。

对于滤波或信号的带宽，最简单的定义即为上下截止频率之差，即频谱非零区间，其它还有功率谱的分布方差(RMS带宽)，以及功率响应的半高全宽等。其中对于半功率带宽，由于功率减半对应分贝数减小3dB，因此也被称为3dB带宽。需要注意的，对于现实的实信号系统，所有讨论都是针对非负频率，因此“带宽”仅为系统双边谱宽度的一半，尤其是对于基带系统，不要混淆。直观地，可将带宽视为携带有效信号的频率范围，尤其是在通信领域。对于实信号系统，负频率冗余，因此带宽仅考虑正频率，对于复信号系统，显然需要考虑双边谱。

实际中，由于高频更易获得大带宽，因此通常会用分数带宽描述系统带通，即带宽除以中心频率。分数带宽与品质因子互为倒数，对于滤波系统，大Q值对应窄带滤波，小Q值对应宽带滤波。

线性系统

根据线性代数，任何有限维度空间内的线性变换都可理解为矩阵乘法$\mathscr{A}x = A x$。将其扩展到连续的无限维函数空间时，向量内积(相乘相加)变为函数相乘积分，而代表线性运算的矩阵将变为核函数，矩阵乘法则变为针对核函数的积分，且根据Schwartz核函数定理，这种线性系统与核函数的对应是唯一的。

$$\mathscr{L}\Bigl\{x(t)\Bigr\} = \int_{-\infty}^{\infty} k(s, t) x(t) dt$$

根据积分的线性性质，显然上述定义的操作属于线性运算。而作为类比：这里可将$x(t)$视为无限维列向量，下标记为$t$；核函数$k(s,t)$是线性系统所对应的无限维矩阵，行列下标分别记为$s$和$t$；而上述积分就是矩阵$s$行与列向量的相乘求和，作为输出向量下标$s$的元素。最后，矩阵的对称性(实数域)在这里对应于$k(s, t) = k(t, s)$，共轭对称性(复数域)则对应于$k(s, t) = \overline{k(t, s)}$。

利用$\delta$函数的平移性质：

$$x(t) = \bigr(\delta * x\bigr)(t) = \int_{-\infty}^{\infty} \delta(t-\tau) x(\tau) d\tau$$

而考虑到线性变换满足结合率：

$$\mathscr{L}\Bigl\{x(t)\Bigr\} = \mathscr{L}\left\{\int_{-\infty}^{\infty} \delta(t-\tau) x(\tau) d\tau \right\} = \int_{-\infty}^{\infty} \mathscr{L}_t\Bigl\{\delta(t-\tau)\Bigr\} x(\tau) d\tau$$

$\delta(t-\tau)$ 为二元函数，$\mathscr{L}_t$ 的下标$t$表示针对$t$进行变换。记$k(t, \tau) = \mathscr{L}_t\Bigl\{\delta(t-\tau)\Bigr\}$，这是线性系统对$\tau$位置单位脉冲函数$\delta(t-\tau)$的响应，同时根据上式，它也是线性系统的核函数。而根据Schwartz核函数定理，线性系统对应的核函数是唯一的。因此，确定了线性系统的核函数，也就得到了系统对单位脉冲函数的响应；反之，找到系统的单位脉冲响应函数，也就确定了描述该线性系统的核函数。

显然，傅里叶变换属于线性变换，对比定义可得其核函数为$k(f,t) = e^{-i2\pi f t}$，而利用上面的性质，核函数为$\mathscr{L}_t\{\delta(t-\tau)\} = \mathcal{F}\{\delta(t-\tau)\}=e^{-i2\pi f \tau}$，两者结论一致。上面介绍的卷积和相关也属于线性变换，核函数分别为$h(\tau - t)$和$h(\tau + t)$。

线性时不变LTI系统(Linear Time-Invariant System)
时不变系统，即不随时间变化的系统，也称平稳系统。对于时不变系统，变换不受时间影响，或者说变换与时间平移可交换。输入时延，输出也相应时延，除此之外系统作用完全一致，最终结果只与输入信号有关，而与信号具体的输入时刻无关。

$$\mathcal{T}\{x(t-t_0)\} = \mathcal{T}\{x(t)\}|_{t-t_0}$$

若前面讨论的线性系统为时不变系统，则系统脉冲响应$\mathscr{L}_t\{\delta(t-\tau)\} = \mathscr{L}\{\delta(t)\}|_{t-\tau}$仅为$t-\tau$函数，系统对应的核函数$k(t, \tau) = h(t-\tau)$。直观理解，核函数仅依赖$t-\tau$，当输入输出变量$\tau, t$同时平移，系统保持不变，系统输出与具体输入时间$\tau$无关。此时：

$$\mathscr{L}\Bigl\{x(t)\Bigr\} = \int_{-\infty}^{\infty} h(t-\tau) x(\tau) d\tau = h(t)*x(t)$$

即，线性时不变LTI系统可由卷积表示。反过来，也可证明，卷积形式的系统是线性时不变的。常见的LTI系统有时延、累加、差分、移动平均以及线性常系数微分/差分方程，二维图像卷积的平移不变形是“时”不变性在空间上的体现。
注意：显然这里$h(t)$不一定是常数，即时不变并不意味系统响应不含时，虽然，响应不含时的系统肯定是线性时不变的。

• 频率响应
  线性时不变LTI系统可由卷积表示$y(t) = h(t) * x(t)$，利用傅里叶变换性质，时域卷积对应频域相乘：

  $$Y(f) = H(f)X(f)$$

  其中$H(f)$为脉冲响应的傅里叶变换，被称为系统的频率响应(frequency response)，反映了系统对不同频率输入的增益。脉冲响应和频响函数分别对应LTI系统在时域和频域的表征。后面会引入Laplace变换作为一般化的时频域变换，脉冲响应的Laplace变换被称为传递函数(transfer function)或系统函数(system function)。
• 本征函数
  函数空间的线性变换本征函数定义为$\mathscr{L}\{v(t)\} = \lambda v(t)$，$\lambda$为本征值。LTI系统的本征函数为复指数函数$e^{i\omega_0t}$：

  $$h(t) * e^{i\omega_0 t} \xleftrightarrow{FT} H(\omega) \delta(\omega-\omega_0)=H(\omega_0) \delta(\omega-\omega_0) \xleftrightarrow{FT} H(\omega_0) e^{i\omega_0 t}$$

  $$\mathscr{L}\{e^{i\omega_0 t}\} = H(\omega_0) e^{i\omega_0 t}$$

  因此$e^{i\omega_0t}$为LTI系统的本证函数，对应本征值$H(\omega_0)$。意味着LTI系统不会引入新的频率，而是只会改变输入信号现有频率成分的幅值(及相位)，周期性函数$\sum_k \alpha_k e^{i\omega_k t}$经LTI系统后变为$\sum_k \alpha_k H(\omega_k)e^{i\omega_k t}$。实际上，根据后面介绍的Laplace变换，对任意复数$s$，复指数函数$e^{st}$都是LTI系统的本征函数。
• 确定LTI系统脉冲响应$h(t)$
  • 直接根据定义：输入脉冲信号，测量系统响应
  • 利用频域特征：输入扫频信号，测量频响曲线$H(f)=\frac{Y(f)}{X(f)}$，逆变换回时域
  • 用信号互相关：输出与输入计算互相关有$r_{yx}(t) = r_{xx}(t) * h(t)$，当输入为白噪声(频谱为常数)$r_{xx}(t)=\delta(t)$，$r_{yx}(t) = h(t)$。

因果系统
因果系统是指具有因果特性的系统，输出仅依赖过去及当前输入，而不依赖未来输入。特别的，若系统输出仅依赖当前输入，则被称为无记忆系统。因为现实物理世界是因果的，任何时域信号的实时处理系统都必须是因果系统，滤波器通常也会被设计为因果的。但非实时处理或图像处理等空间变换(不含时)，并不要求系统具有因果性。无论是否为线性系统，脉冲响应仅依赖过去及当前脉冲输入是系统为因果系统的充要条件。对于线性时不变系统，这意味脉冲响应函数$h(t)=0, \forall t<0$。

FIR v.s. IIR

前面对于线性滤波的讨论都是从频域出发，比如基于频域响应$H(f)$，划分了低通、高通、带通等类别，而基于时域的脉冲响应函数$h(t)$还可将滤波划分为：

• 有限脉冲响应FIR(Finite impulse response)：脉冲响应持续时间有限

  $$y[n] = \sum_{i=0}^N b_i x[n-i]$$

• 无限脉冲响应IIR(Infinite impulse response)：脉冲响应持续时间无限

  $$y[n] = \frac{1}{a_0}\left(\sum_{i=0}^P b_i x[n-i] + \sum_{j=1}^Q a_j y[n-j]\right)$$

有限脉冲响应FIR，即脉冲响应会在有限时间内变为0。上面的卷积表达式为离散的因果FIR滤波，但原则上FIR滤波可以是连续的、也可是非因果的($i<0$)。其中$N$为离散FIR的阶数，对于N阶FIR，持续N+1采样点；$b_i$为滤波器的系数，也是滤波系统在第$i$个时间点的脉冲响应，$h[n] = b_n, n \in [0,N]$，除此之外的时间，脉冲响应为0。对上面的表达式进行Z变换有$Y(z) = \sum_{i=0}^N b_i z^{-i} X(z)$

$$H(z) \equiv \frac{Y(z)}{X(z)} = \sum_{i=0}^N b_i ~ z^{-i}$$

无限脉冲响应存在反馈回路，理论上可无限持续，如最简单的$y[n] = y[n-1]$，实际中通常会逐渐衰减。上面表达式的递归形式就对应于反馈，其中$1/a_0$的系数显得有点奇怪，但上述表达式可改写为$\sum_{i=0}^P b_i x[n-i] = \sum_{j=0}^Q a_j y[n-j]$，其中$P$为前馈滤波的阶数，$b_i$为对应滤波系数，$Q$为反馈滤波的阶数，$a_j$为对应滤波系数。两边同时进行Z变换，考虑到时延特性有$\sum_{i=0}^P b_i z^{-i} X(z) = \sum_{j=0}^Q a_j z^{-j} Y(z)$，从而系统频域传递函数为

$$H(z)\equiv \frac{Y(z)}{X(z)} = \frac{\sum_{i=0}^P b_i ~ z^{-i}}{\sum_{j=0}^Q a_j ~ z^{-j}} = \frac{\sum_{i=0}^P b_i ~ z^{-i}}{1 + \sum_{j=1}^Q a_j ~ z^{-j}}$$

最后一项是因为$a_0$通常取1，而一般情况总可以约化为该形式。

FIR的优势在于不存在反馈，相对简单稳定，且舍入误差不会累积。此外系数对称情况下，其引入的相位延迟为线性的，所有频率延迟为单一确定值，这对于需考虑相位的通信及信号分析等情况很重要。其缺点在于要达到相同的滤波效果，尤其频谱过渡锐利的情况，FIR相比IIR通常需要更高的阶数，意味着更大的计算量及内存需求。设计时通常要针对目标效果进行最优化分析，设计难度相对高。

相对的，IIR的优势在于通常可以用更低的阶数实现滤波要求，意味着更低的计算量以及时间延迟(阶数低)。其设计相对简单，可近似模拟电路效果，如用于音频信号的均衡器等。其缺点在于由于反馈回路的存在，相对不稳定，使用时需要格外注意数值稳定性，且具有非线性的相位延迟，不同频率延迟不同。更多具体对比可参考该链接。

积分变换

上面介绍了函数空间中线性变换被定义为针对核函数的积分，这些变换更常见的名字是积分变换，其他常见的还有拉普拉斯(Laplace)变换及希尔伯特(Hilbert)变换等。
拉普拉斯(Laplace)变换
傅里叶变换建立了时域与频域的联系，但这里的时间与频率都限制为实数域。考虑到指数上的虚数单位$i$，频率可理解为对应频域的虚轴。即傅里叶变换只是时间轴到复频域虚轴的变换，而虚轴之外还有广阔的复数域，将傅里叶变换扩展到复频域就是Laplace变换：

$$\mathcal{F}\{x(t)\} = \int_{-\infty}^{\infty} x(t) e^{-i\omega t} dt \xrightarrow{\boxed{i\omega \rightarrow s=\sigma+i\omega} } \int_{-\infty}^{\infty} x(t) e^{-st} dt = \mathcal{L}\{x(t)\}$$

$$\boxed{X(s) = \int_{-\infty}^{\infty} x(t) e^{-st} dt, ~~~ x(t) = \frac{1}{2\pi i} \int_{\sigma-i\infty}^{\sigma+i\infty} X(s) e^{st} ds}$$

其中复频域$s=\sigma+i\omega$通常被称为$s$平面或$s$域。当$\sigma=0$，考虑到$ds=id\omega$，上述变换就回归了傅里叶变换。即傅里叶变换是沿虚轴的Laplace变换，这也是工程领域傅里叶变换被记作$X(i\omega)$的由来(实际上会用$j$，$i$被用于表示电流)：即可理解为用于区分傅里叶变换与Laplace变换，也可理解为$s=i\omega$的Laplace变换，两者完全一致。

为什么要引入Laplace变换？
Laplace变换将傅里叶变换由实变函数拓展到了复变函数，但有什么好处呢？由时域到频域的傅里叶变换可大幅简化很多运算，比如卷积变为乘法(卷积定理)，微分变相乘、积分变相除(导数定理)，微积分方程变为代数方程。这种时域与频域对偶在数学上属于调和分析的研究内容，这里我们局限于函数变换，傅里叶变换存在要求函数绝对可积，这使得很多问题无法借助时域与频域的对偶性进行处理，Laplace变换扩充了频域，放宽了对目标函数的限制，扩展了可处理问题的范围，在系统控制及微分方程求解等中有广泛应用。
直观理解，Laplace变换相比傅里叶变换多了$e^{-\sigma t}$因子，即便函数$f(t)$发散，只要速度不过快$|f(t)| {\footnotesize\le} Me^{c|t|}$，$t{\scriptsize >}0$时，$\sigma$取值够大就可以压低函数值，使积分收敛。$t{\scriptsize <}0$时要求刚好相反，需要$\sigma$取负值，因此常见的Laplace变换都是只考虑非负区间，即单边形式：

$$X(s) = \int_0^{\infty} x(t) e^{-st} dt = \int_{-\infty}^{\infty} x(t)u(t) e^{-st} dt$$

其中$u(t)$为单位阶跃函数。不加定语的Laplace变换默认指的通常是单边形式，而之前的形式则为称为双边Laplace变换，借助$u(t)$可由双边变换得到单边变换。最后，值得注意的，Laplace逆变换是固定实部$\sigma$的线积分，即只需要找到使积分收敛的$\sigma$即可进行变换。

• Z变换
  对于离散序列的Laplace变换，将目标域由$s$变换为$z=e^{sT}$即为Z变换：

  $$\int_{-\infty}^{\infty} x(t) e^{-st} dt \xrightarrow{t=nT} \sum_{-\infty}^{\infty} T x(nT) e^{-s~nT} \xrightarrow{z=e^{sT}} T\sum_{-\infty}^{\infty} x_n z^{-n}$$

  其中$\sum x_n z^{-n}$就是离散序列$x_n=x(nT)$的Z变换。可以看到Z变换本质就是离散序列的Laplace变换(相差了个倍数T)，区别在于对应的复频域由$s$平面变换到了$z$平面或$z$域。转换的优势在于$z=e^{sT} = e^{\sigma T} e^{i\omega T}$：$s$平面的竖线(平行于虚轴、固定实部$\sigma$)被投影为$z$平面绕原点半径$e^{\sigma T}$的圆，进而可用到复变函数的留数定理。值得注意的，$s$平面的虚轴对应$z$平面单位圆，负实部区域对应单位圆内部，正实部区域对应单位圆外部。

  具体的，参照DTFT，利用泊松求和公式有，离散序列的Laplace变换$X(s)$关于虚轴的$\omega$呈周期性，周期为$\frac{1}{T}$，逆变换对$\omega$的积分只需要限制在一个周期区间，对应到$z$平面意味着绕原点逆时针旋转一周，最终：

  $$\boxed{X(z) = \sum_{-\infty}^{\infty} x_n z^{-n}, ~~~ x_n = \frac{1}{2\pi i} \mathop{\rlap{$\mkern5.5mu\circlearrowleft$}\int} X(z) z^{n-1} dz}$$

  其中逆变换中的积分为绕原点逆时针方向的环路积分。当$s$的实部$\sigma=0$，对应于$z$平面的单位圆，上述变换就回归了DTFT，而DFT则相当于进一步在$z$平面的单位圆上进行采样。

• Mellin变换(梅林变换)
  将Laplace变换中的$t$变量代换为$e^{-t}$即可得到梅林变换：

  $$\int_{-\infty}^{\infty} x(t) e^{-st} dt \xrightarrow{\tau=e^{-t}} \int_{\infty}^{0} x(e^{-\tau}) \tau^s \frac{d\tau}{-\tau} = \int_{0}^{\infty} \tilde{x}(\tau) \tau^{s-1} d\tau$$

  $$\boxed{X(s) = \int_{0}^{\infty} x(t) t^{s-1} d t, ~~~ x(t) = \frac{1}{2\pi i}\int_{\sigma-i\infty}^{\sigma+\infty} X(s) t^{-s} d s}$$

  Mellin变换本质还是Laplace变换，且目标域保持不变，其优势在于$t$的平移对应于$e^{-t}$的缩放，傅里叶变换具有平移不变性，相应的梅林变换具有缩放不变性($s$沿虚轴)：$\mathcal{M}\{x(at)\} = a^{-s}\mathcal{M}\{x(t)\}$，当$s$为纯虚数，$|\mathcal{M}\{x(at)\}| = |\mathcal{M}\{x(t)\}|$。此外，对于$e^{-t}$，梅林变换就是Gamma函数$\Gamma(s) = \int_{0}^{\infty} t^{s-1} e^{-t} d t$，并由此关联到其他相关特殊函数。

最后，可以看到Laplace、Fourier、Mellin以及Z变换本质上都是同一个事物，只是具体场景不同。由于各自主要的应用领域和解决的具体问题有所区别，历史中的发展也基本相对独立，最终造就了各自迥异的名字，未能反映内在的统一性。

希尔伯特(Hilbert)变换

对实信号有$X(-\omega) = \overline{X(\omega)}$，负频率信息是冗余的。利用单位阶跃函数消除其负频率部分有：$X_{+}(\omega)=2X(\omega)u(\omega)$，其中$u(\omega)$形式为：

$$u(\omega) = \frac{1}{2}\Big[1+\text{sign}(\omega)\Big] = \begin{cases} 1 &\text{if } \omega>0 \\ 0.5 &\text{if } \omega=0 \\ 0 &\text{if } \omega<0 \end{cases}$$

这种情况下，$X_{+}(\omega)$没有负频谱，正频率谱密度为$4\frac{|X(\omega)|^2}{Nf_s}$；而$X(\omega)$单边谱为$2\frac{|X(\omega)|^2}{Nf_s}$，谱密度为原来的两倍，下面会看到上述变换在原实信号基础上引入了功率相等的虚部。

对$X_{+}(\omega)$做逆傅里叶变换，相乘变为卷积，$1$对应$\delta(t)$，${\rm sign}(\omega)$对应$\frac{i}{\pi t}$，最终：

$$x_{+}(t) = x(t) * \left[\delta(t) + \frac{i}{\pi t}\right] = x(t) + i ~ x(t)*\frac{1}{\pi t}$$

即消除负频率后对应的时域信号为复信号，实部为原信号$x(t)$，虚部为$x(t)*\frac{1}{\pi t}$。该复信号被称为解析信号(analytic signal)，其虚部则被定义为实部的Hilbert变换。注意解析信号不是普通的复信号，其核心是没有负频率。解析信号的实部和虚部通过Hilbert变换关联，两者相互正交、幅值相同、相位错$\pm\frac{\pi}{2}$。Hilbert变换是由实信号(双边谱)得到对应解析信号(单边谱复信号)的工具，反过来由解析信号得到了对应的实信号，取其实部即可。

下面具体分析Hilbert变换本身的性质：

$$\boxed{\mathcal{H}\{x(t)\} = x(t) * \frac{1}{\pi t} = \frac{1}{\pi}\int_{-\infty}^{\infty}\frac{x(\tau)}{t-\tau} d\tau, ~~~ \mathcal{H}^{-1} = -\mathcal{H}}$$

从频域理解，$\frac{1}{\pi t}$的傅里叶变换为：

$$\frac{1}{\pi t} \xleftrightarrow{FT} \sigma_H(\omega)=-i~\text{sign}(\omega)\begin{cases} -i=e^{-i\frac{\pi}{2}} &\text{if } \omega>0 \\ 0 &\text{if } \omega=0 \\ i=e^{i\frac{\pi}{2}} &\text{if } \omega<0 \end{cases}$$

根据卷积定理：

$$\mathcal{H}\{x(t)\} = \mathcal{F}^{-1} \{X(\omega) \sigma_H(\omega)\}$$

因此Hilbert变换会使原信号的相位移动$\pm\frac{\pi}{2}$，具体的：正频率平移$-\frac{\pi}{2}$，负频率平移$+\frac{\pi}{2}$。信号的幅度不变，且相位移动后与原信号正交。

最后，介绍下解析信号的性质及应用：
解析信号用复数的模长与幅角表示有：$x_{+}(t) = |x_{+}(t)|e^{j\phi(t)} = a(t)e^{j\phi(t)}$
其中$a(t)$被称为信号的瞬时振幅，对应于实信号的包络线；$\phi(t)$被称为信号的瞬时相位，对应于是信号的相位角。瞬时相位的导数被称为瞬时角频率$\omega(t) = \dot{\phi}(t), \phi(t) = \theta + \int_0^t \omega(t) dt$，而瞬时频率$f(t) =\frac{1}{2\pi}\omega(t)$。
解析信号的瞬时幅度、频率和相位可用于绘制时频谱，分析信号的局部特征，尤其是对于非平稳信号，具体参考时频谱中的希尔伯特-黄变换。其次，瞬时幅度、相位、频率信息可用于调制信号的解调，此外基于Hilbert变换还可在调幅中实现单边带调制，减少能耗和带宽占用。

注意，幅角相差整数倍的$2\pi$并不影响最终信号，因此直接计算信号幅角，返回的都是位于$(-\pi, \pi]$或$[0, 2\pi)$区间的主值，即经过折叠的相位(wrapped)，而计算瞬时频率显然要用未经折叠的(unwrapped)相位，因此需要对相位进行展开(解卷绕)。展开的核心是降低序列中相邻元素的绝对差值，最大容许的差值通常为周期的一半或自定义取值(需大于周期一半)。Numpy中可使用unwrap可进行相位展开，默认周期为$2\pi$，对于输入序列，所有大于$\pi$的不连续性都会通过加减整数周期进行修正。

傅里叶变换反映的是一段时间内的平均值，而解析信号的振幅与频率则是瞬时值。
显然对于普通的正余弦信号，其对应的解析信号瞬时频率和瞬时振幅就是信号本身的频率与相位。

傅里叶变换是一个全局估计，它告诉了我们观测信号整个时间段里的一个综合表现。

上面介绍的都是连续的核函数$k(\tau, t)$，还有一些积分变换会使用一系列离散核函数$k_n(t)$，类似于周期函数的傅里叶级数，常见的是各种正交的多项式序列，如基于厄米特(Hermite)多项式的厄米特变换，基于雅可比(Jacobi)多项式的雅克比变换等。

时频谱 Spectrogram

在普通的傅里叶变换中，信号的时域特征与频率特征不可兼得，对于稳态信号频域特征或许是足够的，但对于快速变化的非稳态信号，通常需要同时考虑频域和时域信息，分析频率成分的同时定位具体出现的时间，时频谱(Spectrogram)是更好的选择。最简单的做法是将信号在时间上均匀划分为小片段，分别进行傅里叶变换，即短时傅里叶变换STFT。计算信号在每个时间片段的功率谱密度即可得到作为时间和频率函数的二维时频谱。其它如小波变换，可以根据频率调整分辨率，对于高频部分增加时间分辨率，对于低频部分则提升频率分辨率，对于快速变化的瞬时信号有较好效果。

https://en.wikipedia.org/wiki/Time–frequency_analysis

短时傅里叶STFT

将信号在时间上均匀划分为小片段，分别进行傅里叶变换，其中时间片段的划分会使用窗口函数$w(t)$实现，最常用的窗口为汉宁(hanning)窗，而使用高斯窗的STFT也被称为Gabor变换。

$$X(\omega, t) = \int x(\tau) w^*(\tau - t)e^{-i\omega \tau} d\tau$$

$$X(k, m) = \sum_n x_n w^*(n - mI)e^{-i\frac{2\pi k}{N} n}$$

$$P(k, m) = \left|\frac{X(k, m)}{\sum w_n}\right|^2, ~ S(k, m) = \frac{|X(k, m)|^2}{f_s\sum |w_n|^2}$$

上式中$I$为窗口移动间隔：由于窗口会压低边缘值，作为补偿窗口间通常存在重叠，而移动间隔等于窗口长度$N$减去窗口重叠长度$O$。随着$m$增加，窗口中心由初始位置向后移动至$mI$，最终总的窗口数为$\left⌊\frac{L-N}{I}\right⌋+1 = \left⌊\frac{L-O}{N-O}\right⌋$。(L - noverlap)//(nperseg - noverlap)

numpy未提供时频谱函数，scipy.signal中计算时频谱的函数有stft和spectrogram两个：前者直接对应(修正后的)STFT谱，默认为离散复值谱$\frac{1}{\sum w_n}X(k, m)$(scaling=‘spectrum’)；后者可返回PSD(默认)、复谱以及幅值、幅角、相位等，两者在默认参数上有所区别，具体参考下面代码的注释。Matplotlib中绘制STFT谱的函数为specgram，大致与spectrogram对应，但默认参数上有所不同。

注意，signal.stft有两个独有参数boundary和padded，默认值分别为’zeros’和True，会改变时间窗数量。窗口函数压低窗口边缘值，重叠可对序列内部实现补偿，但无法处理边界，通过延拓可将序列起点移至窗口中心。boundary用于控制延拓行为，‘even’/'odd’延拓值关于端点偶/奇对称，'zeros’对应取0，'constant’取端点值，'None’对应不延拓。padded用于控制是否补零，以使序列刚好对应整数窗口，即(L - nperseg)/(nperseg - noverlap)为整数。注意延拓是首尾对称进行的，而补零则只在序列末尾。

import numpy as np
from scipy import signal
from matplotlib import pyplot as plt

fs = 1e4
t = np.arange(0, 1, 1/fs)
f = 500 + 300*np.sin(2*np.pi*3*t)
s = np.sin(2*np.pi*f*t)
# s = np.sin(2*np.pi*np.cumsum(f)/fs)
win = signal.windows.hann(256)

### 绘图 ###
def spectrogram_plot(freqs, times, psd, ax, **kwargs):
    # imshow的extent为边界范围，与像素中心坐标差半格
    pad_t = (times[1]-times[0]) / 2
    t_min = times[0] - pad_t
    t_max = times[-1] + pad_t
    pad_f = (freqs[1]-freqs[0]) / 2
    f_min = freqs[0] - pad_f
    f_max = freqs[-1] + pad_f
    extent = t_min, t_max, f_min, f_max

    Z = 10*np.log10(psd)
    ax.imshow(Z, extent=extent, aspect='auto', origin='lower', **kwargs)
    #ax.pcolormesh(times, freqs, Z)

fig, axes = plt.subplots(2, 1)
psd, freqs, times, _ = axes[0].specgram(s, Fs=fs, sides='twosided')
spectrogram_plot(freqs, times, psd, axes[1])
plt.show()

### plt.specgram v.s. signal.spectrogram/stft ###
# plt.specgram: window=np.hanning, NFFT=256, noverlap=128, detrend=None
def spectrogram_shift(freqs, psd):
    freqs = np.fft.fftshift(freqs)
    psd  =  np.fft.fftshift(psd, axes=0)
    return freqs, psd

# window=('tukey', 0.25), nperseg=len(window)|256, noverlap=nperseg//8
freqs1, times1, psd1 = signal.spectrogram(s, fs=fs, nperseg=256, noverlap=128, 
                            detrend=False, window=win, return_onesided=False)
freqs1, psd1 = spectrogram_shift(freqs1, psd1)
print(np.abs(psd - psd1).max())

# stft为复频谱，且相比spectrogram有不同的默认参数取值及两个特殊参数
# window='hann', nperseg=256, noverlap=nperseg//2, detrend=False
# boundary='zeros', padded=True, scaling='spectrum'
freqs2, times2, spec2 = signal.stft(s, fs=fs, window=win, return_onesided=False,
                            boundary=None, padded=False, scaling='psd')
freqs2, psd2 = spectrogram_shift(freqs2, np.abs(spec2)**2)
print(np.abs(psd - psd2).max())

注意，相位与频率关系为$\phi(t) = \int \omega(t)dt, \omega(t) = \dot{\phi}(t)$，因此$\sin\left( \omega(t) t\right)$对应频率为$\omega(t) + \dot{\omega}(t)t$而非$\omega(t)$，以$\sin\left(\sin(t)t\right)$为例，对应频率为$\sin(t)+\cos(t)t$，对应上例中频率震荡范围随时间增加。

由于时频分析中不确定性原理的限制，时域分辨率和频域分辨率不可兼得，两者不确定性存在下限$\Delta t\Delta \omega > 1/2$(Gabor极限)。因此实际中通常需要在时间与频率分辨率之间进行平衡，对于变化更快的高频信号会希望有更高的时间分辨率，而对于变化缓慢的低频信号则只需要较低的时间分辨率。STFT的主要缺点是其时间及频率的分辨率固定，完全由时间片段划分(时间窗口的宽度)决定，而无法随信号的频率成分自适应改变。

小波变换Wavelet (~ Morlet et al. 1981)PyWavelets

傅里叶变换本质是信号在函数空间的展开，而空间的基函数是不同频率的正余弦函数$e^{-i\omega t}=e^{-i\pi f t}$。小波变换则是将基函数替换为(正交)“小波”(wavelet)，之所以叫“小波”是因为相较于无限延伸的正余弦函数，后者只存在于有限的时间区间。正余弦函数由于在时间上不是定域的，可以分析信号的频率成分却无法确定对应的时间区间，以“小波”作为基函数则不存在该问题。作为基函数的小波是由母小波$\psi(t)$经过平移缩放得到的一系列函数$\psi_{a,b} = \frac{1}{\sqrt{a}}\psi(\frac{t-b}{a})$，其中$a, b$分别为缩放/尺度(scale)和平移(shift)因子。母小波常见的有Morlet、墨西哥帽(Mexican hat)、多贝西(Daubechies)、哈尔(Haar)等。

# !pip install PyWavelets
import pywt
import matplotlib.pyplot as plt
continuous_wavelets = ['morl', 'mexh']
discrete_wavelets = ['db2', 'Haar']

list_list_wavelets = [continuous_wavelets, discrete_wavelets]
list_funcs = [pywt.ContinuousWavelet, pywt.Wavelet]

fig, axarr = plt.subplots(nrows=2, ncols=2, figsize=(8,8))
for row, list_wavelets in enumerate(list_list_wavelets):
    func = list_funcs[row]
    for col, waveletname in enumerate(list_wavelets):
        wavelet = func(waveletname)
        if row == 1:
            scaling_function, wavelet_function, x_values = wavelet.wavefun()
        else:
            wavelet_function, x_values = wavelet.wavefun()
        if col == 0 and row == 0:
            axarr[row, col].set_ylabel("Continuous Wavelets", fontsize=16)
        if col == 0 and row == 1:
            axarr[row, col].set_ylabel("Discrete Wavelets", fontsize=16)
        axarr[row, col].set_title(f"{wavelet.family_name}", fontsize=16)
        axarr[row, col].plot(x_values, wavelet_function, linewidth=2, color='k')
        axarr[row, col].set_yticks([])
        axarr[row, col].set_yticklabels([])

plt.tight_layout()
plt.savefig('demo.png', transparent=True)
plt.show()

$$W(a, b) =\int x(t) \psi^*_{a,b}(t) dt, a>0 ~~~ \leftrightarrow ~~~~ x(t) = \frac{1}{C_\psi a^2} \iint_{a>0} W(a, b) \psi^*_{a,b}(t)~da db$$

容许条件(admissibility condition)：小波变换逆变换中的系数$C_\psi = \int \frac{|\Psi(\omega)|^2}{|\omega|} d\omega$ 其中$\Psi(\omega)=\int \psi(t)e^{-2i\omega t} dt$，是小波母函数的傅里叶变换。该系数有限是小波变换的容许条件。容许条件暗含$|\Psi(\omega)|$衰减速度比$|\omega|^{-1/2}$快，且$|\Psi(\omega)|_{\omega=0} =0$，从而小波函数的谱具有带通滤波形式。同时由傅里叶变换$\Psi(0) = \int \psi(t) dt = 0$，即要求$\psi(t)$必须是波动函数。

正则条件(regularity conditions)：要求小波在时域和频域均平滑且集中(衰减快)，通常用消失距进行表示。小波函数的$n$阶距定义为$M_n\{\psi\} = \int t^n \psi(t) dt$，小波函数最高几阶距为0，就称其有几个消失矩。对信号进行泰勒展开，其小波变换$W(a, 0) = \int \sum_n \frac{x^{(n)}(0)}{n!} t^n \frac{1}{\sqrt{a}} \psi(\frac{t}{a}) dt = \frac{1}{\sqrt{a}} \sum_n \frac{x^{(n)}(0)}{n!} ~ a^{n+1} \int t^n \psi(t) dt$。对于具有$n$个消失距的小波函数，任意平滑信号的小波变换将随尺度因子的$n+2$阶衰减(?)。对消失距的要求根据具体应用确定。

与普通STFT得到的时频谱相比，小波变换中小波函数本身就兼具窗口函数的功能，且窗口宽度可变：随着缩放因子$a$的增加，小波被拉伸，时间窗口增加，同时震荡频率减低。因此在小波变换的时频谱中随着频率增加，时间分辨率增加、频率分辨率降低，相比STFT中固定的时频分辨率，小波变换可根据频率自适应的调整分辨率，对变化越快(频率越高)的成分，使用越精细的时间粒度进行分辨。同样受限于不确定性原理，无法同时提升时间和频率分辨率，实际小波分析中时频窗口面积由具体的小波母函数决定。

注意，由于小波并非周期函数，不存在确定的频率，相较于傅里叶变换获取信号的不同频率成分，小波变换是在不同尺度上审视信号。因此小波变换得到的时频谱通常会使用尺度因子(scale)代替频率作为纵轴，也被称为Scaleogram。不过使用母函数的中心频率除以尺度因子可以得到“伪频率”(pseudo-frequency)，变换回频域绘制通常的时频谱。

小波变换继承和发展了STFT的局部化思想，事实上Morlet小波变换与Gabor变换(高斯窗口的STFT)在数学上等价：Morlet小波本质上就是平面波(正余弦函数)与高斯窗口的叠加，因此也被称为Gabor小波。不同之处在于，Gabor变换为STFT，时间窗口固定，Morlet小波变换则是其多分辨(multiresolution)变种，通过尺度因子实现了时间窗口随频率的自适应变化，很好的平衡了时域与频域信息。

连续小波变换CWT将信号转换到时频域时存在较多信息冗余，为减少计算量更常用的是离散小波变换DWT，后者小波函数中的尺度与平移因子取为离散值，最常见的选择是二分采样(dyadic sampling)：尺度因子每次增加为之前2倍(频率↓)，平移间隔也对应增加为之前2倍(采样率↓)，$a = 2^j, b= k 2^j, \psi_{j,k} = \frac{1}{\sqrt{2^j}}\psi(\frac{t-k2^j}{2^j})$，时间采样率随频率下降降低。根据 Nyquist 采样定理，这样可在不损失信息的前提下，最大限度的降低冗余，变换后的时频信息可以实现信号的恢复重建。

离散小波变换中，每个小波函数只能覆盖特定频率区间，且随频率降低，对应区间也逐渐缩小，为避免无限迭代，又引入了尺度函数(scaling function)，用于覆盖特定截止频率以下的所有频率区间。使用尺度函数代替小波函数，忽略了部分尺度信息，理论上存在信息丢失，但实际上并不会影响信号的重建(?)。

最后，离散小波变换通常会实现为迭代滤波器组(filter bank)：信号频谱被分为高频和低频两部分，对应信号中细节与整体信息，高频部分由小波函数对应的高通/带通滤波器(HP)提取，低频部分则由尺度函数对应的低通滤波器(LP)提取；之后对于低频部分，经下采样后，再次二分处理，提取细节信息，依次迭代分解，如下图所示。直至信号的分解结果符合要求，或达到最大分解层级(样本数少于滤波器宽度)。在这一过程中，信号被分解到多个子频带进行处理，通常被称为子带编码(subband coding)。在迭代过程中，带通滤波器的中心频率及宽度逐层减半，同时信号也随之进行下采样，与二分采样的离散小波变换相对应。

STFT是对时间分片，不同时间片段信号的变换并不相关；DWT则是对频率分带，需要处理全部时间的信号，每次提取特定频率(尺度)的成分，从最小的尺度开始，由高频到低频逐步降低频率(同时对数据下采样)。从滤波器角度看，STFT是整体均匀的频带划分，DWT则是对低频部分迭代二分，形成树状的滤波器组。

离散小波变换中，随频率降低尺度因子增加，一般取为对数均匀，最常见的是尺度因子依次翻倍(指数增长)、频率带宽减半(分辨率提升)，同时相应的减半时间采样率。

Q变换Q-Transform(Brown J. 1991) librosa.cqt

在离散小波变换中，频率通常取为对数均匀，如前面的二分采样。在这样的实现下，每个频带的中心频率与频带宽度之比(Q值)为常数，也被称为常数Q变换。Q变换最初由Brown J.提出，用于处理音乐信号，因为音阶所对应的频率为对数均匀，Brown据此提出了
一系列滤波(filter)，(中心)频率与带宽成正比，频率分布对数均匀，而相应的带宽随着频率增长而增加，两者比例保持不变。

$$X(t, \omega) = \int x(\tau) w^*(\tau - t, \omega)e^{-i\omega \tau} d\tau$$

与普通STFT相比，这里窗口函数是频率的函数：其宽度与频率成反比。实现上则通常基于傅里叶变换：将信号的傅里叶变换频移后与频域窗口函数相乘，之后再逆傅里叶变换。尤其是在离散变换中，可借助快速傅里叶变换的计算优势。

$$X(t, \omega) = \int \tilde{x}(\phi + \omega) \tilde{w}^*(\phi, \omega)e^{i\phi f} d\phi$$

$$X(m, n) = \sum_k x_k w^*(k - m)e^{-i\frac{2\pi k}{N} n}$$

$$X(m, n) = \sum_k x_k w^*(k - m, n)e^{-i\frac{2\pi k}{N} n}$$

STFT中窗口函数不随频率(n)改变而改变，Q变换中窗口随频率而变

Some wavelet transforms are also considered to be constant Q transforms because in the discrete versions of the transforms, the scale of the wavelet is varied exponentially (base being 2 in this case).

A property of wavelet transforms is that they have build in the constant Q-factor property, or in other words logarithmic scaling.

其他时频分析方法

• S变换 S-Transform / Stockwell Transform (Stockwell 1994)
  S变换同样是具有自适应窗口宽度的STFT，其窗口函数为高斯函数(Gabor变换)，同时相较于普通的高斯窗口，其窗口宽度(标准差)$\propto 1/|\omega|$，随频率增加而缩小。同时由于归一化因子中的$|\omega|$项，S变换倾向于强调高频成分。
  S变换是Q变换的一种，但不符合小波变换的要求
  具有小波变换类似的自适应分辨率，同时具有全局的相位参考测量??
  globally referenced phase and frequency measurements

$$ST_x(t,\omega) = \int x(\tau) |\omega| e^{-\pi (\tau-t)^2 \omega^2} e^{-i\omega\tau} d\tau$$

• 韦格纳分布Wigner Distribution(Wigner 1932)

$$W_x(t, \omega) = \int x(t + \frac{\tau}{2})x^*(t-\frac{\tau}{2}) e^{-i \omega \tau} d\tau$$

• Hilbert-Huang变换
  https://en.wikipedia.org/wiki/Hilbert–Huang_transform
  Hilbert变换+EMD经验分解
  Hilbert变换算法要求输入信号只能是线性稳态的。非线性非稳态

time frequency amplitude 时频谱 Hilbert谱
https://zhuanlan.zhihu.com/p/25250010
IF是一个正值函数，则信号本身有同样多的过零点和极值点。
IF有负值，则信号在相继的过零点间有多个极值。

经验模态分解EMD(Empirical Mode Decomposition)对简单信号的定义为本征模函数IMF（Intrinsic Mode Functions），满足两个要求，第一要震荡，极值点的个数和过零的个数相等或差1，第二，任何一个点都有局部的关于零的对称性。EMD方法可以说是自适应信号处理方法的代表方法，他开创了自适应数据驱动分解方法分析的时代。现有大量研究者在自适应信号处理领域耕耘，不过很遗憾，该方法到目前为止还没有理论基础。但是，该方法的实验研究表明，该方法具有广泛的通用性，同时开辟了自适应信号处理新领域，大量自适应信号处理方法都基于EMD的思想。例如（ITD，SWT，EWT，VMD，NSP等等方法）。

各IMF为平稳态分量，且包含了原信号的不同时间尺度的局部特征

经过EMD分解出的IMF分量再经过Hilbert变换，最终得到信号瞬时频率和瞬时幅值”的方法叫做希尔伯特黄变换（HHT，Hilbert-Huang Transform）。
The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis

时频分析与小波变换-台大

---

The Story of Wavelets
An Introduction to Wavelets
Jean Morlet and the Continuous Wavelet Transform (CWT)
High Resolution Time-Frequency Representations for RF Signals
Fourier, Gabor, Morlet or Wigner: Comparison of Time-Frequency Transforms

A Really Friendly Guide To Wavelets
A Really Friendly Guide To Wavelets