深度学习入门

深度学习大讲堂 中科视拓 刘昕(CEO)
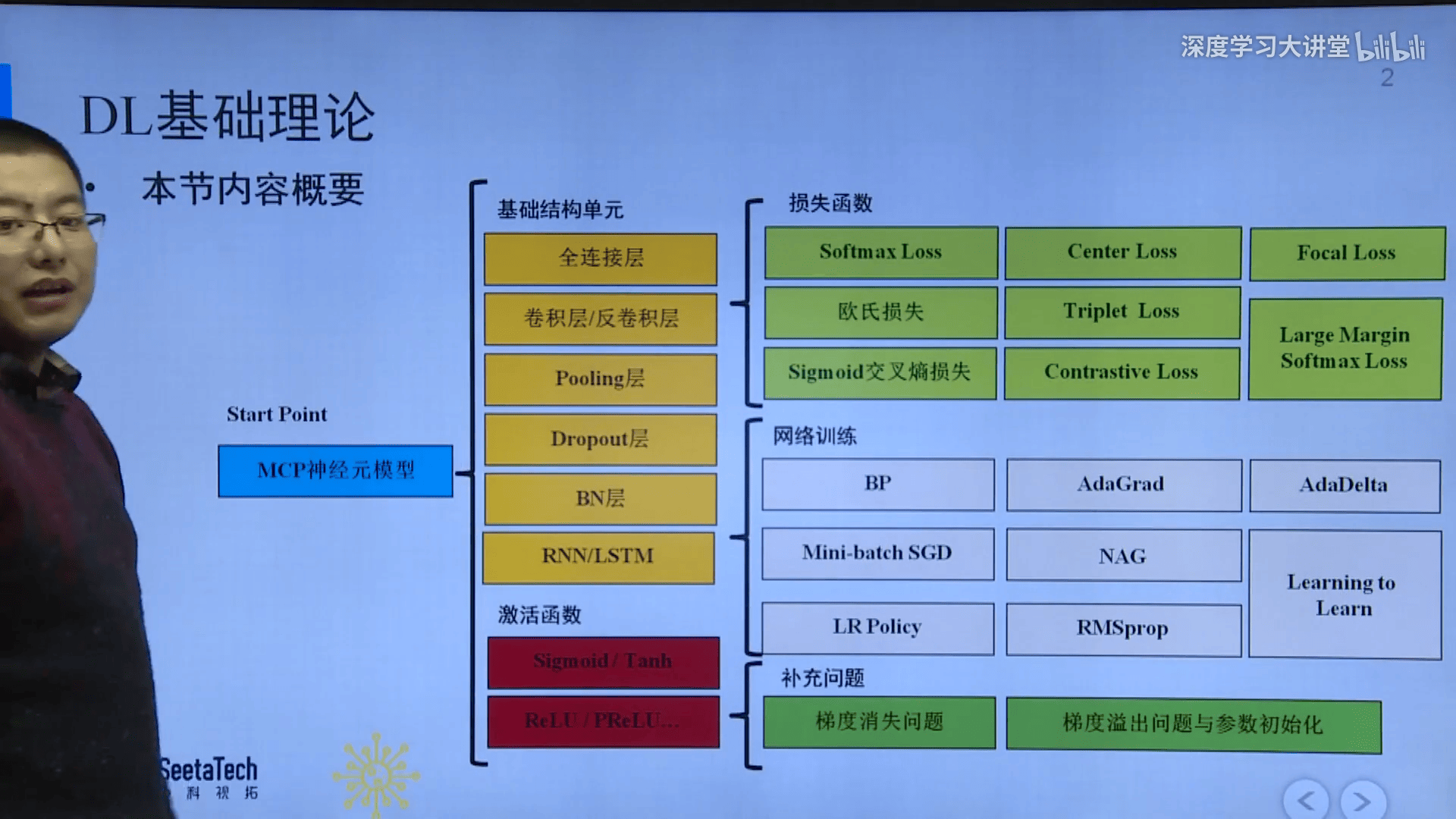
数学基础、DL简史、基础结构、CNN演化

数学基础

微积分

• 梯度消失：sigmoid激活函数导数 ≤ 1/4，多层嵌套后导数 → 0
• 拉格朗日中值定理、泰勒展开 柯西中值定理、洛必达
• 凸函数 ⇔ 一阶导单调增(二阶导 ≥ 0) 凸凹加个负号就可转换，但凸与非凸且非凹不能转换

向量微积分

• 向量范数：0范数、1范数 → 稀疏编码 (sparse coding)；2范数||x||² = x^Tx
• 线性组合、线性相关/无关、线性空间、基矢、线性表示
• 线性变换、矩阵、 逆变换、逆矩阵、相似矩阵、特征值、特征向量
• 特殊矩阵：对称矩阵$A=A^T$、厄米特矩阵$A=A^*$ (A^*为A的共轭转置)
  　　　　　正交矩阵$A^TA=AA^T=I$、幺正矩阵/酉矩阵$A^*A=AA^*=I$；
  　　　　　正规矩阵$AA^T = A^TA, ~ AA^* = A^*A$；
  　　　　　正定矩阵$\forall x \in \R^n \setminus 0, x^T A x >0$ (通常限定于对称/埃尔米特矩阵)
  　　　　　幂等矩阵$A^2=A$、幂零矩阵 $\exists n \in \N^+, ~{\rm s.t.} A^n =0$
  正交矩阵具有保范性：不改变向量长度(2范数)，只是对向量进行旋转及(或)镜像翻转。幺正矩阵则是正交矩阵向复矩阵的推广。
  正规矩阵必可对角化(谱定理)，对称(厄米特)阵、正交(幺正)阵都是正规阵。对称阵可实现实数域的对角化，正交矩阵则只能保证复数域上的酉对角化(特征值为复数)。
• 奇异值可直观理解为方阵特征值向一般矩阵的推广。需注意的是奇异值根据定义是非负的，而特征值无此要求。对于方阵，如果是正规矩阵，则奇异值就是特征值的绝对值；一般情况，两者则可能有较大差异，但奇异值的最大与最小值给出了特征值绝对值的上下界。只有秩为0的矩阵奇异值才全为0，特征值则不一定，如幂零矩阵。
  $\begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 3 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix}$ 幂零矩阵，秩为3，特征值全为0，但奇异值为0, 1, 2, 3；
  $\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}$与$\begin{bmatrix} 0 & 2 \\ 1/2 & 0 \end{bmatrix}$特征值均为-1, 1，但奇异值前者为1, 1，后者为1/2, 2。
• 将矩阵视为作用在向量上的算子(线性变换)，其“长度”(2-范数)伸缩性就由最大奇异值决定，更严格的可定义矩阵的算子范数；而矩阵行列式则对应变换的“体积”伸缩因子。对方阵，还有谱半径的概念，定义为最大的特征值绝对值，从前面的例子可知，谱半径并不能作为伸缩性的限制，不过对正规矩阵而言谱半径就是算子范数。
• 奇异值分解：$A=U\Sigma V^\ast$，其中$U\in\R^{m \times m}$, $V\in\R^{n \times n}$为正交矩阵，$V^\ast$为$V$的共轭转置，$\Sigma \in \R^{m\times n}$为对角矩阵，对角元为奇异值。正交矩阵具有保范性：不改变向量的长度(2范数)，只是对向量进行旋转及(或)镜像翻转。因此，通过奇异值分解将矩阵$A$中实现伸缩及投影的核心部分 $\Sigma$ 给提取了出来，知乎上的这个分析不错。
• 正交矩阵及幺正矩阵具有保范性：它们的特征值绝对值/奇异值都是1(复数需取模)。
• 矩阵分解：三角分解(LU)、QR分解、特征值分解/谱分解、奇异值分解SVD
• 向量微积分：1阶(Jacobi矩阵)、2阶(Hessian矩阵) → 梯度、(向量函数)泰勒展开
  卷积 → 向量内积，而非矩阵乘法 → 相似度, 特征提取(参考下文卷积层部分)
• 布局约定：向量微积分中一个易引起困惑的问题是矩阵是否需要转置，而本质在于对$\dfrac{\partial \bm{y}}{\partial \bm{x}}, \bm{y}\in \R^m, \bm{x}\in \R^n$表示形式的约定，其结果可表示为$m \times n$或$n \times m$的矩阵，两者相差一个转置，造成困惑的原因在于很多人会混用两种形式。
  • 分子布局：保持分子$\bm{y}$的(列向量)布局，分母$\bm{x}$转置，对应$m \times n$矩阵
  • 分母布局：保持分母$\bm{x}$的(列向量)布局，分子$\bm{y}$转置，对应$n \times m$矩阵
• 本文中统一用分子布局，在这样的布局约定下有一些地方需注意，如损失函数$\mathcal{L}(y)$的导数$\frac{\partial \mathcal{L}}{\partial y}$是一个行向量，激活函数$y = a(z)$的导数$\frac{\partial y}{\partial z}$是一个对角矩阵${\rm diag}(a'(z))$。
• 从张量角度理解：$d_{ij} = \frac{\partial y_i}{\partial z_j}$，$a$为逐元素操作，因此$i\not=j$时导数为0，$d_{ij}$为对角阵。如果考虑到数据的矢量化，$x$为数据列向量组成的矩阵，$y,z$相应也为矩阵，$d_{ijkl} = \frac{\partial y_{ij}}{\partial z_{kl}}$，同样由于$a$为逐元素操作，只有$i=j,k=l$时取值非0。这个高阶张量该怎么理解？对应的计算是什么？怎么约化到普通二维矩阵？
  这里问题本质其实是逐元素操作(elementwise)的函数的导数，相比矩阵对矩阵求导更简单：微分规则为$dy=a'(z)\circ dz$，其中$\circ$为逐元素相乘(Hadamard product)，而$a'(z)$为逐元素求导，并非通常意义上的导数$\frac{dy}{dz}$(矩阵对矩阵求导)。
  神经网络涉及的另一运算是逐元素相乘相加(Frobenius product)“$\small A:B$"或”$\small\lang A,B\rang_F$"(复数需取共轭)，也可理解为将矩阵展开为一维向量做内积。${\rm tr}(A^T B)=A:B$
  对向量而言就是正常内积，而单个矩阵的元素和可表示为$1:A$。总损失函数显然就是预测值$y$与实际值$\bar{y}$的逐元素操作后的求和，$\mathcal{L}(y,\bar{y})=1:L(y,\bar{y})$，其中$L(y,\bar{y})$对应逐元素操作。该最终结果为标量，$d\mathcal{L} = \frac{\partial L}{\partial y}:dy$，即逐元素相乘相加的微分运算与通常意义的偏导数间是可以直接变换的。
  最后，$\small A: (B \circ C) = (A\circ B) : C)$，由此$d\mathcal{L} = \frac{\partial L}{\partial y}:dy = \frac{\partial L}{\partial y}: a'(z) \circ dz = \frac{\partial L}{\partial y} \circ a'(z) : dz \equiv \frac{\partial L}{\partial z}:dz$，从而$\frac{\partial L}{\partial z} = \frac{\partial L}{\partial y} \circ a'(z)$，跳过$\frac{\partial y}{\partial z}$直接得到了$\frac{\partial L}{\partial z}$。
  Rewrite matrix derivative with element-wise
  Derivative of matrix equation with elementwise term

凸优化

凸集、凸函数 ⇔ 一阶导单调增(二阶导 ≥ 0) ⇔ Hessian矩阵半正定 ⇔ ∀x≠0, x^TAx≥0
f 为凸函数 ⇔ 定义域D_f为凸集，且∀x,y ∈ D_f, f (y) ≥ f (x) + ∇f(x)^T (y-x) ⇔ ∇²f (x)半正定

对偶问题

一般优化问题：

$$\begin{aligned} \min ~ & ~ f(x)\\ {\rm s.t.} ~ & ~ g_i(x)\le 0, i = 1, .., m;\\ & ~ h_j(x)=0, j = 1, .., p.\\ {\rm with} & ~ x \in D_f \subseteq \R^n \end{aligned}$$

⇔

对偶问题：

$$\max_{\mu \ge 0, ~ \lambda} ~ l(\mu, \lambda)$$

$l(\mu, \lambda)$为拉格朗日对偶函数，具体定义如下。

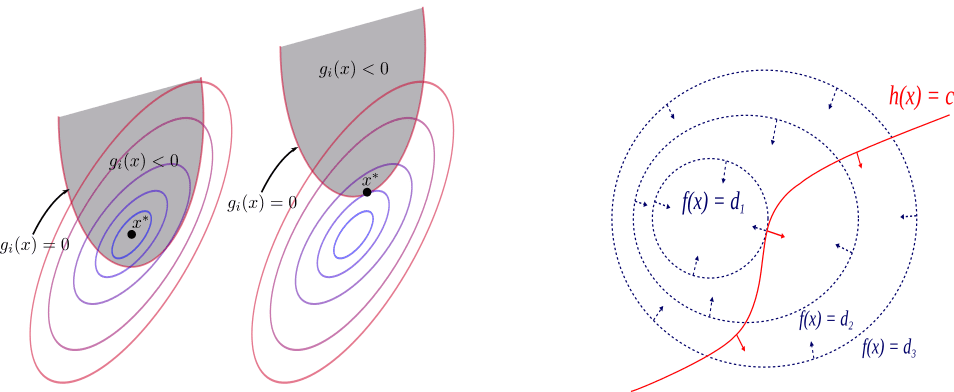
• 拉格朗日函数：

$$L(x,\mu, \lambda)=f(x) + \mu^Tg(x) +\lambda^Th(x); \mu \ge 0 (\in \R^m), \lambda \in \R^p$$

• 拉格朗日对偶函数：

$$l(\mu, \lambda) = \inf_{x \in D_f} L(x, \mu, \lambda)$$

• 其中$\mu, \lambda$为拉格朗日乘子，也称对偶变量。引入拉格朗日乘子(函数)的目的在于将复杂边界的约束优化问题转化为通常更易于处理的无约束或简单边界约束的优化问题( Lagrangian relaxation )；而将原问题转换为对偶问题好处则在于后者必然是凸优化。
• 对偶函数定义为对$\forall x \in D_f$求$L(x, \mu, \lambda)$的下确界。而对任意给定的$x$，$f(x)$, $g(x)$, $h(x)$取值固定，$L(x, \mu, \lambda)$其实是关于$\mu, \lambda$的仿射函数，不同$x$对应不同仿射函数。即对偶函数$l(\mu, \lambda)$是对由无数仿射函数构成的函数集合$\{l_{x_1}, l_{x_2}, ...\}$逐点求下确界，结合凹函数定义易知$l(\mu, \lambda)$必为凹函数，而无需考虑$f(x)$, $g(x)$, $h(x)$的凸凹性。由此无论原问题是否为凸优化，对偶问题一定可化为凸优化。
• 简单来说，原问题和对偶问题分对应拉格朗日函数的minmax与maxmin：

$$\min_{x \in D_f} \max_{\mu \ge 0,~ \lambda} L(x,\mu, \lambda) \leftrightarrow \max_{\mu \ge 0,~ \lambda} \min_{x \in D_f} L(x,\mu, \lambda)$$

• 假设原问题最优(小)取值为$p^\ast$，则$\forall \mu \ge 0, \lambda, l(\mu, \lambda) \le p^\ast$，即对偶问题的最优值$d^\ast$给出了原问题最优值$p^\ast$的下界(minmax ≥ maxmin)。
• 原问题与对偶问题的等价性 → 强对偶条件：Slater条件(充分)、KKT条件(必要)
  扩展阅读：约束优化方法之拉格朗日乘子法与KKT条件

凸优化算法
实际目标/损失函数通常为非凸的，凸优化算法仍可使用，但不能确保实现全局最优。

• 一阶：梯度下降、随机梯度下降SGD、批梯度下降BGD、小批量SGD(mini-batch SGD)
  • η步长/学习率调整：线搜索 (line search)、按一定策略衰减 (learning rate decay) step, exponential, …
  • 权重衰减(weight decay)：损失函数中引入L2正则项，效果是梯度下降权重更新时有额外衰减项；
  • 动量(Momentum)：当前梯度之外以移动平均(moving average)方式引入历史梯度信息(momentum)进行修正。隐式扩大了所使用的batch size，降低batch随机性的干扰，使梯度下降更加平稳，加速收敛。
• 二阶：牛顿方法、拟牛顿方法DFP, BFGS, LBFGS
  • 牛顿方法 H^-1J ：需计算Hessian矩阵(的逆)，本身计算量大，且Hessian矩阵不一定半正定(凸函数条件)
  • 拟牛顿方法：不计算二阶导的前提下，构造出可近似Hessian矩阵的半正定矩阵 → 拟牛顿条件
  • 参考：https://blog.csdn.net/itplus/article/details/21896453
• 神经网络的训练可以采用二阶优化方法吗？
  对于深度学习而言，由于模型参数量巨大，二阶方法中梯度计算的时间(计算)及空间(存储)复杂度都较大；其次，二阶方法优势在于高精度时的优化速度，而深度学习对参数精度要求并不高，二阶的优势无法展现；最后，实践中常采用mini-batch等技巧，基于少量随机样本的局部估计替代全局估计，二阶方法更易陷入鞍点(?不确定)；综上，虽然有研究进行尝试，但实践中通常不会在深度学习中使用二阶优化方法。

历史简介

AI简史

智能：目标导向的自动感知与决策
萌芽：图灵测试(1954) [通用AI ↔ 专项AI]
起源：达特茅斯会议(1956)
历史：符号推理(计算机代数系统) → 专家系统(知识图谱) → 深度学习
前沿：图像(CV)、语音文字(NLP)、专家系统/知识图谱、强化学习(RL)
应用：实时翻译、自动驾驶、辅助医疗、辅助教育、金融风控/投资、推荐系统、媒体生成

更详细的历史可参考：https://www.aminer.cn/ai-history/

神经网络

• 视皮层 层级感受野假设：视野范围从小到大、功能简单到复杂(线条→简单图案→复杂图案)
• 生物学实验(1962) → 多层感知机MLP(1969) → BP算法(1974, 1982, 1986) → 万能逼近定理(1989)：任何闭区间内的连续函数，都可以用包含隐含层的BP网络来逼近 → 卷积神经网络CNN(1989, 2012) → 生成对抗网络GAN(2014)
• CNN：LeNet(1989 BP+SGD)、AlexNet(2012 GPU, ReLU, dropout, data augmentation)、VGG(2014)、GooLeNet(2015)、ResNet(2015 skip connections)、DenseNet(2017)

思想变迁

• [非线性]核方法、流形学习 → 深度网络
• 分治策略 → 端到端学习，减少人的干预
• 算法驱动 → 数据驱动，从数据获取知识
• 人工设计特征 → 自动学习特征
• AutoML

未来预期

• 专家知识驱动 → 监督大数据驱动 → 数据+知识驱动，用知识减少对数据的需求
  AI算法 + 算力 + 大数据 → AI算法 + 算力 + (大)数据 + 知识(知识/常识的表示与利用)
• 出生时的大脑是大数据(历代祖先)学习的结果；后天的脑发育则是利用小数据和知识对进化脑进行微调的过程。
• 专项AI集成协同？单模态到多模态？通用AI？
• 可解释性

DL简史

• 两段式(特征工程+ML算法) → 深度网络端到端学习(特征提取与分类/回归协同优化)
• 定义：以不少于两个隐含层的NN对输入进行端到端的非线性变换或表示学习的技术
• 结构：MLP(全连接)、CNN、RNN/LSTM、GAN
  
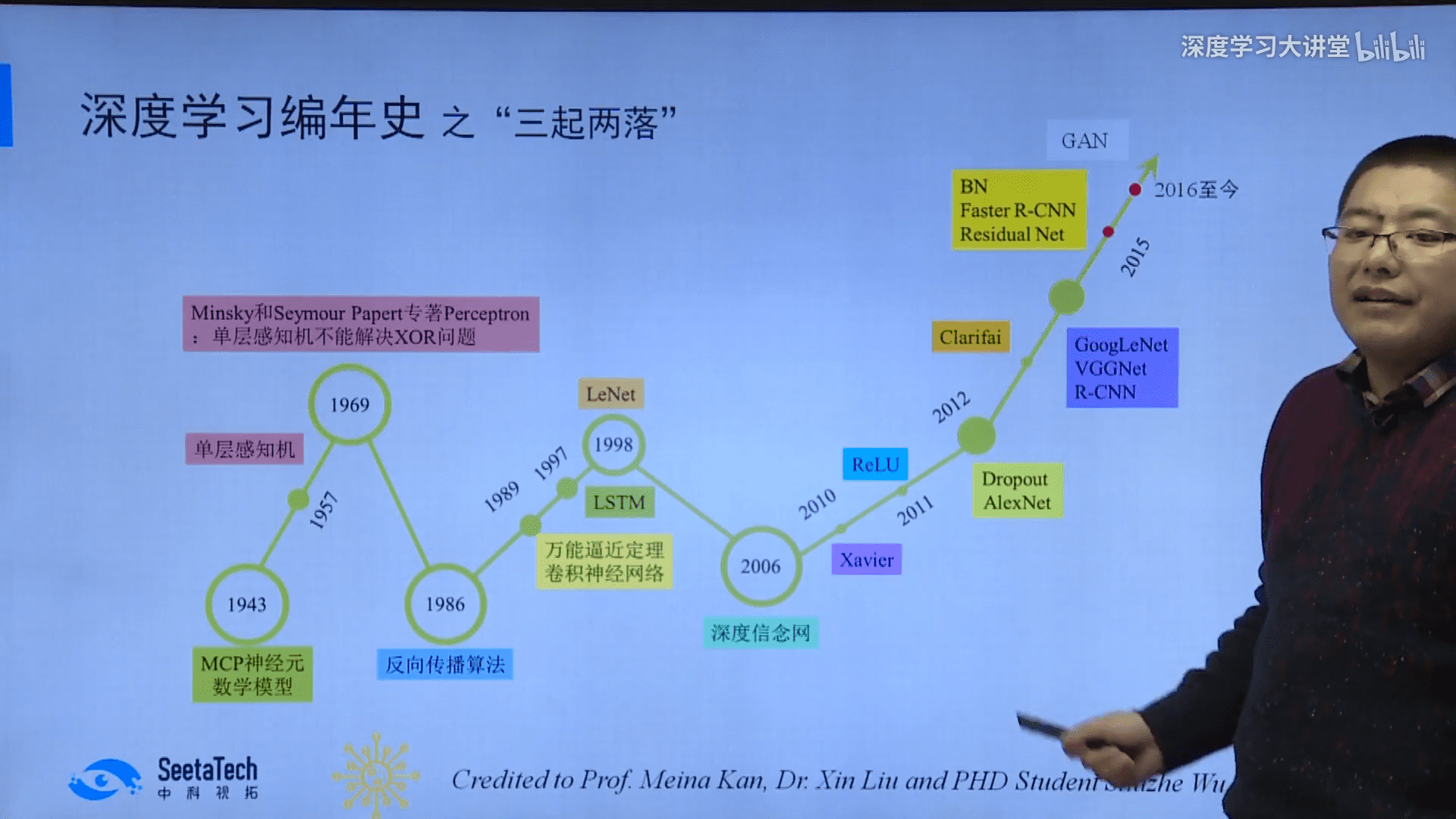
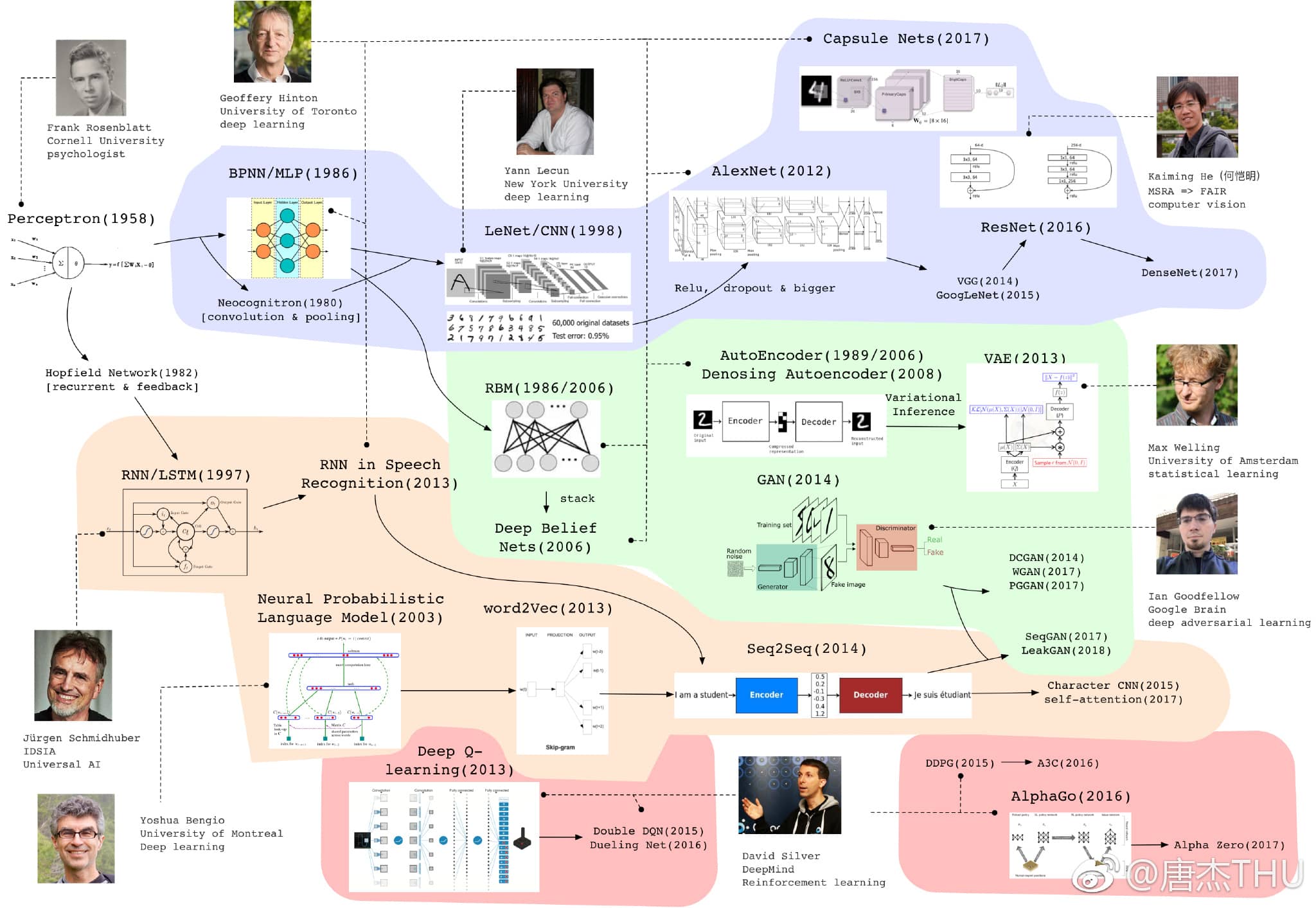
• 单神经元MCP(1943) → 单层感知机SLP(1957) → 多层感知机MLP(1969) → BP算法(1974, 1982, 1986) → 万能逼近定理(1989) → 卷积神经网络CNN(1989) → 循环神经网络RNN(Jordan Network 1986, Elman Network 1990) → 长短时记忆LSTM(1997) → 深度信念网络DBN(2006) → 生成对抗网络GAN(2014)
  更全面的历史可参考：https://weibo.com/2126427211/GavUQjfLa
• DL之前：决策树、SVM、Boosting、稀疏编码、图模型、LDA子空间学习、流形学习
• 始于2006的复兴：分层预训练(layer-wise pre-training)解决了梯度消失导致的训练困难(但之后随着ReLU的出现不再需要)，出现了深度信念网络DBN、深度玻尔兹曼机DBM、深度自编码器DAE
• Xavier(2010) 深度网络参数初始化、ReLU(2011) 梯度消失
• AlexNet(2012): ReLU、Dropout、GPU、Data Augmentation
• BatchNormalization(2015) 深度网络收敛速度提升5~20倍
• 进展：加深(ResNet)、分类到检测分割(R-CNN, FCN, FPN, Mask R-CNN)、新功能单元(GAN)
• 未来：网络结构设计的自动学习、脏乱差数据学习、GAN的工业应用
  

基本结构

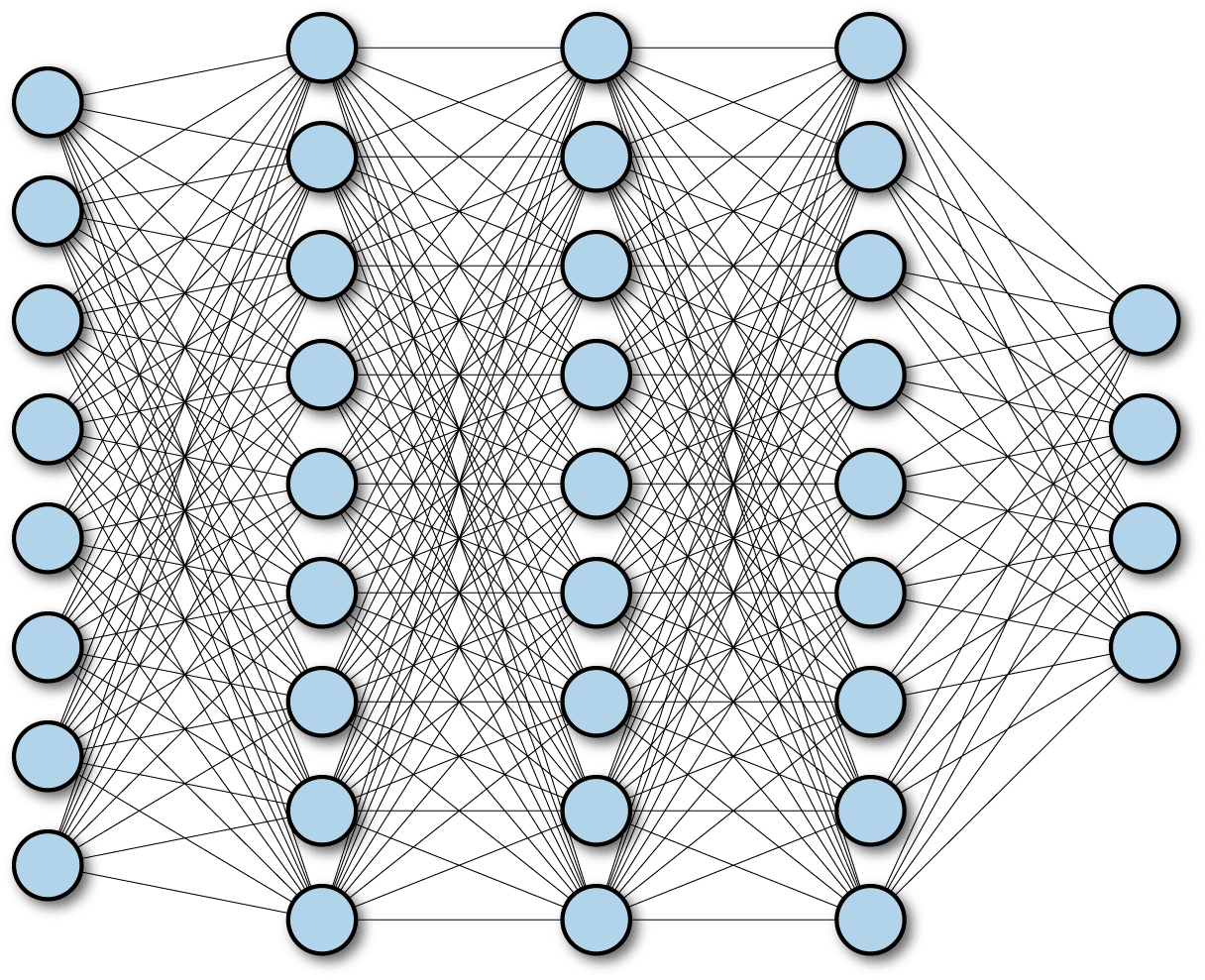
全连接

输出层的神经元和输入层的每个神经元都相连
Forward: $z = wx + b, y = a(z)$, $a$ is the activation function.
Backward: $\frac{\partial \mathcal{L}}{\partial w}=x \frac{\partial \mathcal{L}}{\partial y} {\rm diag}(a'(z)), \frac{\partial \mathcal{L}}{\partial x} = \frac{\partial \mathcal{L}}{\partial y}{\rm diag}(a'(z)) w, \frac{\partial \mathcal{L}}{\partial b}= \frac{\partial \mathcal{L}}{\partial y}{\rm diag}(a'(z))$
　　　　 $\frac{\partial \mathcal{L}}{\partial w}=x \frac{\partial \mathcal{L}}{\partial y} \circ a'(z), \frac{\partial \mathcal{L}}{\partial x} = \frac{\partial \mathcal{L}}{\partial y} \circ a'(z) ~ w, \frac{\partial \mathcal{L}}{\partial b}= \frac{\partial \mathcal{L}}{\partial y} \circ a'(z)$

卷积层

卷积核作为输入矩阵上的滑窗，依次与相对应patch(展开为向量后)做内积
Forward: $z = w^{\rm flip} * x + b = w \otimes x + b \rightarrow \sum_k\sum_l w_{k,l}x_{i+k,j+l} + b_{ij}, y = a(z)$
　　　　多通道：$z = \sum_c w_c \otimes x_c + b \rightarrow \sum_c\sum_k\sum_l w_{k,l,c}x_{i+k,c,j+l,c} + b_{ij}$
Backward: $\frac{\partial \mathcal{L}}{\partial w}= \frac{\partial \mathcal{L}}{\partial y} a' \otimes x, \frac{\partial \mathcal{L}}{\partial w_{k,l,c}}=\sum_i\sum_j\frac{\partial \mathcal{L}}{\partial y_{i,j}} a'_{i,j} x_{i+k,j+l,c}$
　　　　 $\sout{\frac{\partial \mathcal{L}}{\partial x} = w * \frac{\partial \mathcal{L}}{\partial y} a', \frac{\partial \mathcal{L}}{\partial x_{i,j}}=\sum_c\sum_k\sum_l w_{k,l,c} \frac{\partial \mathcal{L}}{\partial y_{i-k,j-l}} a'_{i-k,j-l}}$
　　　　 $\frac{\partial \mathcal{L}}{\partial x} = w^{\rm flip} \otimes \frac{\partial \mathcal{L}}{\partial y} a', \frac{\partial \mathcal{L}}{\partial x_{i,j}}=\sum_c\sum_k\sum_l w^{\rm flip}_{k,l,c} \frac{\partial \mathcal{L}}{\partial y_{i+k,j+l}} a'_{i+k,j+l}$
　　　　 $\frac{\partial \mathcal{L}}{\partial b}= \frac{\partial \mathcal{L}}{\partial y} a'$
特点：稀疏连接(与全连接相对)；权值共享(每个输出通道共享一个卷积核)
　　　 → 极大减少了参数量(计算量)

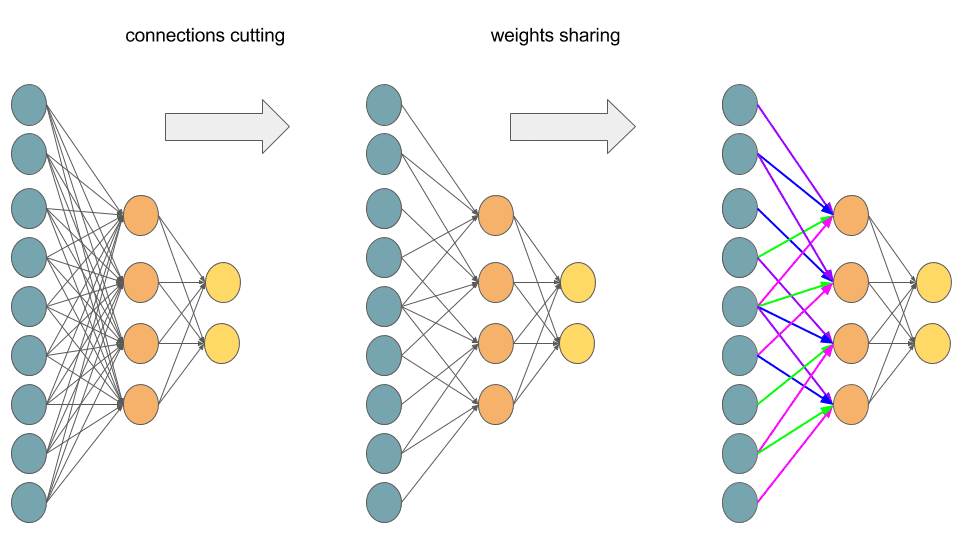
实际实现中通常是基于im2col技巧(numpy.lib.stride_tricks.sliding_window_view, torch.nn.Unfold)将输入的patch及卷积核全部展开，转化为全连接再进行运算。

卷积：$f*g~(x,y) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(u,v)g(x-u,y-v)dudv$
离散形式：$f*g~(i,j) = \sum_{k} \sum_{l} f(k,l)g(i-k,j-l)$

相关：$f \otimes g~(x,y) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(u,v)g(x+u,y+v)dudv$
离散形式：$f \otimes g~(i,j) = \sum_{k} \sum_{l} f(k,l)g(i+k,j+l)$

$f(k,l) \to \hat{f}(k,l) = f(-k,-l)$可实现卷积与相关的转换，对矩阵而言这意味着上下左右翻转(flip)。CNN实现中，方便起见通常将卷积核视为已翻转过的，因此执行的实际上是互相关操作，但根据惯例仍称之为卷积。

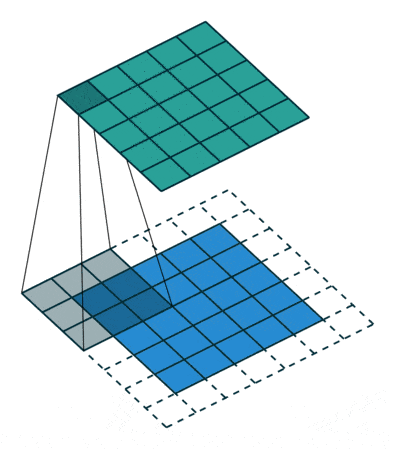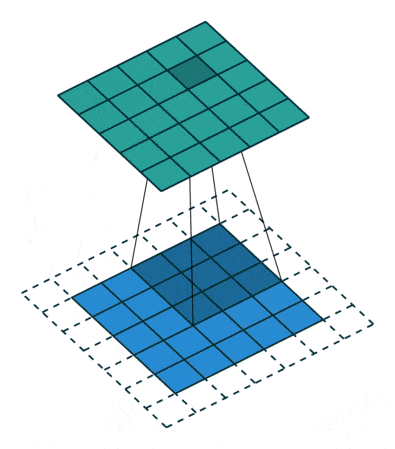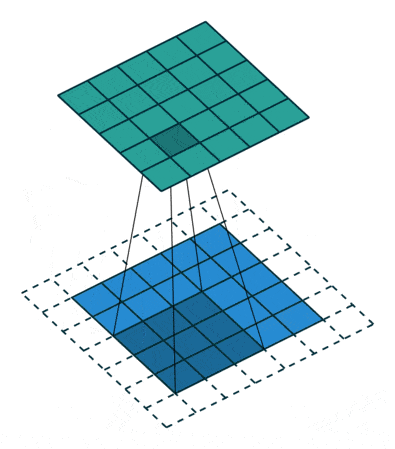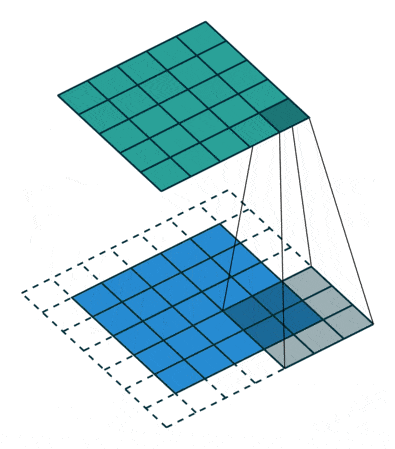
卷积操作：随$i,j$变化，卷积核在输入矩阵上移动，与对应的patch逐元素相乘相加，作为输出矩阵$(i,j)$元，该操作直观理解相当于将卷积核及对应patch分别展开(flat)为一维向量，并执行向量内积，因此结果反映的是patch与卷积核所代表特征模式的相似度，而卷积操作是进行特征扫描提取的过程。最后通过层层卷积，就可实现由底层特征依次组合出更高层特征；而换个角度，越深的网络层，每个卷积核在初始输入矩阵中所关联的范围也将越大，即视野范围越广，从而可以提取更高层的特征。
卷积操作会使输入矩阵大小逐渐缩小，对于实现深层网络这将是个问题，通常的做法是在矩阵四周填充0(padding)，这样做还同时提升了边界元素的贡献，其中不加padding的被称为valid，而通过填充使(步长为1时)尺寸保持不变的被称为same。此外卷积操作会对所有通道(channel)累加，为维持通道数量，通常会使用多个卷积核，各自独立操作，每个卷积核对应一个输出通道(feature map)。
注1：输入尺寸n×n，卷积核k×k，填充p，步长s，输出尺寸⌊(n+2p-k)/s⌋ + 1。其中same填充保持尺寸不变的前提是步长s=1，即填充 p = (k-1)/2。在其它步长下，same填充p取值不变，从而输出尺寸将变为⌈n/s⌉
注2：课程中老师说的卷积核个数为输入通道数×输出通道数是将卷积核限定为二维矩阵$w_{k,l}$，但通常多通道时会将三维矩阵$w_{k,l,c}$视为一个卷积核，从而卷积核数目就是输出通道数。

理论上卷积网络是可以处理不同尺寸的输入，但受限于网络结构尺寸设计，实际情况可能并不理想。比如当输入尺寸过小，可能造成最终输出的特征图非常小，大量信息丢失，表示能力下降。为更好适应不同尺寸输入，网络结构还需要一些特殊的设计，如检测任务中的金字塔池化可使输出特征尺寸不受输入尺寸影响，分割任务中的全卷积网络可使得输出尺寸与输入始终一致。

3×3, 5×5, 7×7，为什么卷积核通常都是奇数的？
进行padding时，可以对称分布；有明确的中心作为移动的位置基准。这篇文章讨论了偶数卷积核。

1×1的卷积有什么用？
卷积操作会对所有输入通道累加，因此对于1×1的卷积核而言，其输出就是所有通道的线性叠加(之后再加上非线性激活)；多个卷积核对应多个输出通道，从而使用1×1卷积核还可以实现通道维度(数量)的升降。综上，1×1的卷积操作以最少的参数实现了跨通道的数据交流(特征融合)以及通道维度调节。最后，换个角度，1×1的卷积就是将通道视为整体的全连接操作。

卷积操作需整合所有输入通道，而1×1卷积能以最少的参数实现该操作，因此为进一步减少网络参数，可将正常卷积“拆解”为不考虑通道方向整合的逐通道(depthwise)卷积与只进行通道整合的1×1卷积两个操作，即深度可分离卷积(Depthwise Separable Convolution)。假设输入通道为C，输出通道为N，卷积核尺寸k×k，则通过这样的拆解：原本要C×k×k×N个参数的卷积变为仅需要1×k×k×C + C×1×1×N个参数，极大的减少了参数数量(当然两者显然不是完全等价的)。该操作是MobileNet构架的核心，用以实现移动及嵌入式环境下的轻量级深度网络。进一步的，我们还可以将上面逐通道的的k×k卷积“拆解”为k×1与1×k卷积两个操作，继续缩减参数量，也被称为空间可分离卷积(spatially separable convolution)。至此，原本由三维矩阵实现的卷积，被替换为由三个一维向量实现的纵向(depthwise k×1)、横向(depthwise 1×k)以及深度方向(elementwise 1×1)的卷积。

类似的操作还有分组卷积，即将输入通道及输出通道分组，组与组之间完全独立。假设分组数为g，则卷积参数将由C×k×k×N变为C/g×k×k×N/g × g，仅为原本的1/g。注意，这里显然需要输入及输出通道数都能被分组数整除。分组卷积最早出现(AlexNet)是因为显卡内存不够，只能将卷积拆分到不同显卡中操作，发现不但减少了参数量，效果也还不错。而最近又重新引起注意，如ResNeXt, ShuffleNet, CondenseNet，用于缩减网络参数(计算量)。

可以看到逐通道(depthwise)卷积正是分组卷积的极端情况，分组数等于输入(出)通道数。分组卷积中各分组间是相互独立的，没有数据交流。这种通道间的相互独立相当于人为引入的结构稀疏性(展开为全连接时为分块对角阵)，减少计算量的同时，还具有正则化效果。但另一方面，通道隔离也会导致精度下降，对于这一问题：ResNeXt参照可分离卷积，在分组卷积后引入1×1卷积进行通道整合；ShuffleNet中通过对通道重新分组(Shuffle)，实现分组之间的数据交流；CondenseNet则通过迭代剪枝自动学习相对合理的分组。

反卷积

卷积的“逆”过程，实现信号尺寸上的恢复(上采样)。这里的“逆”加引号是因为反卷积只是尺寸上的恢复，并不能这能真正恢复到卷积前的状态，信息是有损的。

反卷积(转置卷积)

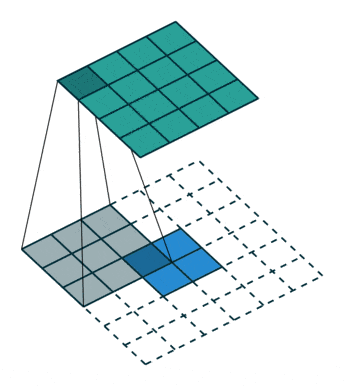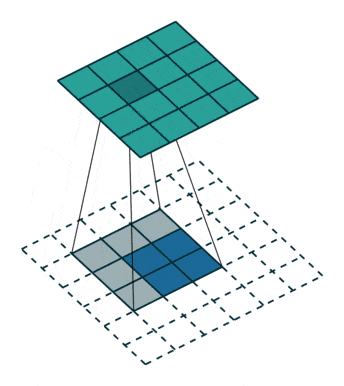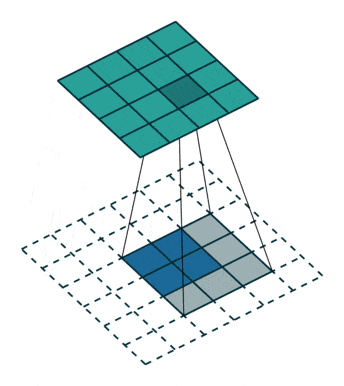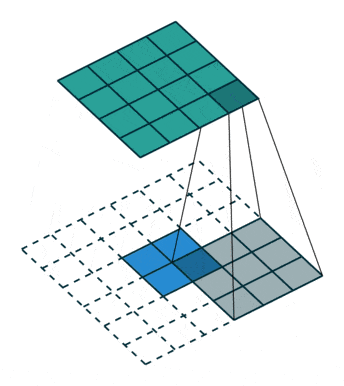
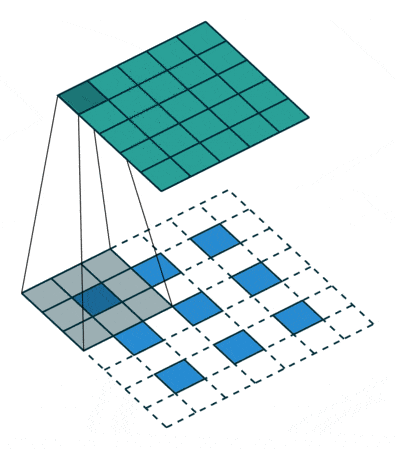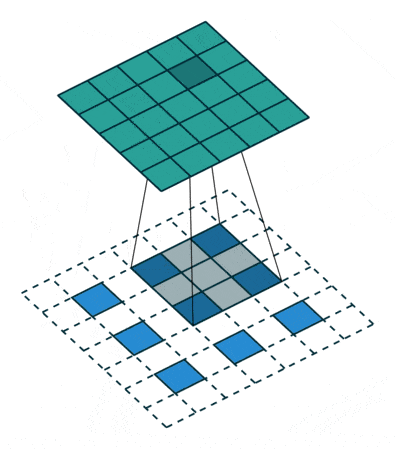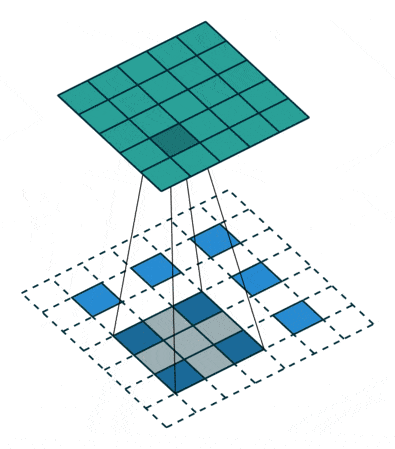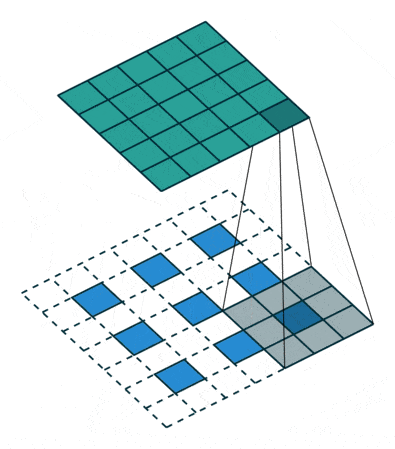
反卷积可理解为一种分数步长的卷积(Fractionally Strided Convolution)：假设卷积过程中步长为s>1，反卷积过程中为了实现尺寸的恢复，就需要卷积步长s’=1/s<1，具体实现上则是在输入元素间插入s-1个0，之后再按普通卷积操作(s’=1)，如上图所示。网上看到有将其翻译为微步卷积，听起来很雅致，却失去了英文很直白的字面含义。两一方面，反卷积也被称为转置卷积，因为将卷积展开为全连接形式(矩阵相乘)，反卷积就相当于卷积核展开后所对应的稀疏矩阵进行了转置，具体的可参考知乎上的讨论。分数步长卷积与转置卷积分别对应了反卷积的两种理解和实现方式，前一种方式实现上相对低效，因此实际中，类似将卷积展开为全连接，反卷积也是展开为全连接(转置卷积)进行计算。
注：卷积输出尺寸为⌊(n+2p-k)/s⌋ + 1，当步长s不为1时，经过取整，不同输入尺寸n可能对应相同的输出尺寸，也就意味着反卷积时，输出尺寸并非唯一确定的，pytorch/keras都提供了额外参数output_padding用于限定输出尺寸。在默认情况下，对于valid填充，卷积输出尺寸⌊(n-k)/s⌋+1，反卷积对应为(n’-1)×s+k；；same填充，卷积输出尺寸⌈n/s⌉，反卷积对应为n’×s。

反卷积具体应用有：FCN中通过反卷积实现上采样，使得输出与输入一致，以实现逐像素的图像语义分割；GAN中通过反卷积来生成图像，典型结构包含反卷积网络(生成器) + 卷积网络(鉴别器)。

卷积与后面的池化都属于下采样，用于实现信息的(有损)压缩，过滤细节，提取核心特征；与之相对的，可通过反卷积、反池化进行上采样，实现信息“量”(如图像尺寸)上的提升。除此之外，插值或外推是最基本的上采样方法。相比插值/外推，反卷积优势在于卷积核可以自动学习调整；局限性也同样在于需要经过学习才能获得合适的卷积核。
反卷积最大缺陷则是输出图像会出现明暗相间的棋盘状网格(Checkerboard Artifacts)。通过确保反卷积核大小被步长整除(避免不均匀重叠)，可在一定程度上缓解棋盘效应，但并不能消除。还可以，先通过插值/外推提升图像尺寸，再进行卷积操作，避免使用反卷积层，这种方法在图像超分辨率中有应用。而且，即使不用反卷积层，所有的卷积层在误差反向传播时也都是反卷积操作，从而会导致梯度计算的棋盘效应。这同样是个问题，比如会导致梯度计算，以至于最终网络结构，更依赖于某些特定位置的像素，不过最终具体影响尚不清楚。

池化层

池化(Pooling)：用池化核对输入特征图进行约化，有最大池化、平均池化及随机池化等。
Forward：[最大池化]取区域最大值；[平均池化]取区域均值；[随机池化]将输入归一化后作为概率矩阵，训练阶段依概率随机选择区域内位置，测试阶段则取加权平均。
Backward：[最大池化]梯度仅由最大值位置反向传播(其它位置为0)；[平均池化]梯度均分；[随机池化]梯度仅由前向传播时(随机)选中的位置反向传播，其它位置为0，类似最大池化。

最大池化保留最强的激活值，能很好的保持图像的边缘和纹理特征，相应的也容易过拟合(low variance, high bias)；而均匀池化则会弱化强激活值，抹平细节纹理，保留背景信息。随机池化在平均意义上与均匀池化接近，而局部意义上又与最大池化接近，而且在训练阶段引入的随机性，相当于训练了很多不同的子网络结构，最终模型为所有子网络的集成平均，从而可以有效防止过拟合。这样看起来，随机池化是最优选择，但实践中还是要根据具体情况测试选择。

卷积 v.s. 池化

• 不同于卷积，池化操作中步长通常是与池化核尺寸相等的，即不重叠；但也某些情况也会使用重叠池化(Overlapping Pooling)；
• 步长大于1的卷积，相当于在步长为1的卷积基础上，对所得到的特征图(feature map)进行了等间隔的下采样，后一操作有点类似池化，不过池化中并没等间隔的池化。

池化层的作用：过滤细节信息，引入特征不变性，使模型更关注是否存在某些特征而非其具体位置，使学习能容忍特征的微小变形(平移、旋转、拉伸等)，防止过拟合，提升特征表示的鲁棒性；同时，下采样降低了数据维度，减少了参数与计算量。而从误差反向传播来看，最大池化能使误差稀疏，平均池化能使误差均摊。
类似反卷积之于卷积，池化也对应有反池化：对最大池化而言，需记录池化所取最大值的位置，反池化时将输入填充在相应位置，其余位置补0；对平均池化而言，直接复制填充即可。

循环单元

RNN：引入历史信息(记忆)，前一时刻的输出会作为当前时刻输入的一部分，即下图中的横向依赖。区别于CNN中相互独立的滑窗卷积操作，这种历史依赖的结构使得RNN可以有效提取时序信息。

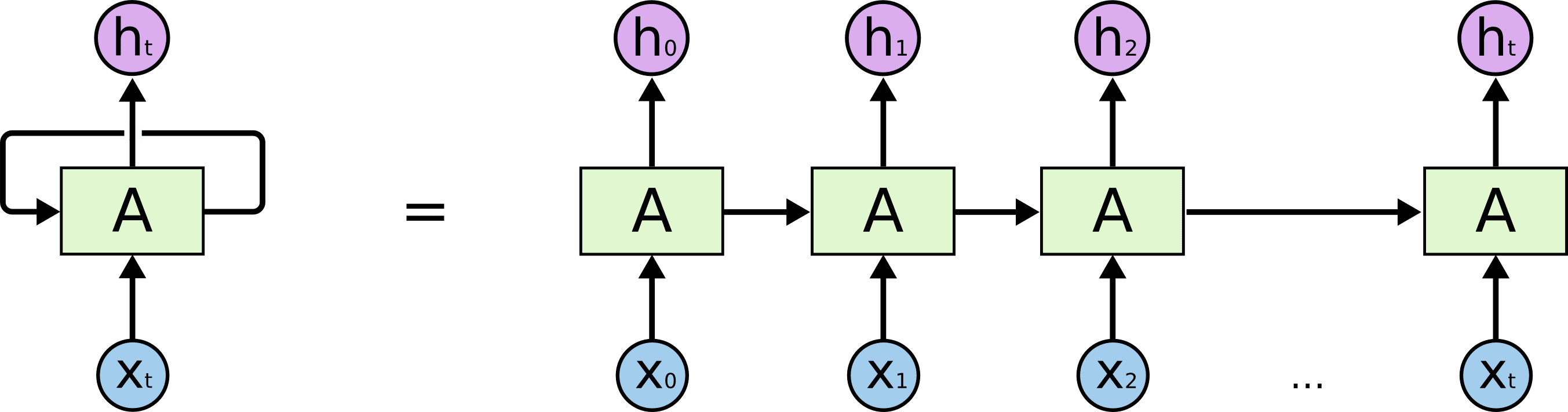
Forward : $\begin{aligned} &\sout{h_t = a(W h_{t-1} + V x_t + b); ~ y_t = Uh_t}\\ &s_t = Wa(s_{t-1}) + V x_t + b; ~ y_t = Ua(s_t)\\ &\mathcal{L} = \sum_{t=1}^\tau\mathcal{L_t} = \sum_{t=1}^\tau\mathcal{L}(y_t) = \sum_{t=1}^\tau\mathcal{L}(Ua(s_t)) \end{aligned}$
其中$a$为激活函数，如$\tanh$，模型参数包括循环权重矩阵$W$、输入权重矩阵$V$及偏置$b$，以下统一以$\theta$表示(输出权重矩阵$U$不参与循环，以下分析不涉及)，注意不同时刻模型的所有参数是共享的。对参数$\theta$求导：
Backward :$\begin{aligned} \frac{\partial \mathcal{L}}{\partial \theta} &= \sum_{t=1}^\tau \frac{\partial \mathcal{L_t}}{\partial \theta}\\ \frac{\partial \mathcal{L_t}}{\partial \theta} &= \sum_{r=1}^t \frac{\partial \mathcal{L_t}}{\partial s_t} \frac{\partial s_t}{\partial s_r} \frac{\partial^{+} s_r}{\partial \theta}\\ \frac{\partial s_t}{\partial s_r} &= \prod_{k=r}^{t-1} \frac{\partial s_{k+1}}{\partial s_{k}} = \prod_{k=r}^{t-1} W {\rm diag}[a'(s_k)] \end{aligned}$
其中$\frac{\partial^{+} s_r}{\partial \theta}$代表对$\theta$直接求导(不向$s_{r-1}$, …追溯)：$\frac{\partial^{+} s_r}{\partial W} = a(s_{r-1}); ~ \frac{\partial^{+} s_r}{\partial V} = x_t; ~ \frac{\partial^{+} s_r}{\partial b} = 1$
由反向传播公式，梯度传播主要受循环矩阵$W$及激活函数$a$影响：

• 先忽略激活函数，由于参数在循环中共享，随序列增长，循环矩阵对系统的影响是指数级的($W^{t-r}$)。矩阵的伸缩性由其最大奇异值决定(参考向量微积分)：若矩阵最大奇异值小于1，则梯度将衰减至0；若矩阵最大奇异值大于1，则梯度将发散。
• 正交矩阵具有保范性(norm-preserving)，如果循环矩阵是正交矩阵就可以保持梯度，而不会出现衰减或发散，此时系统主要受激活函数影响。
• 而激活函数的效果通常是收缩的，${\rm diag}[a'(s_k)]$最大奇异值对Sigmoid而言不超过1/4，tanh不超过1，ReLU则大概率是1，因此ReLU可以有效改善梯度消失的问题。

为什么RNN及变种都默认用tanh做激活函数，而非能改善梯度消失ReLU？
对于反向传播，梯度消失能用ReLU改善，梯度爆炸可以进行裁剪(Clipping)，因此RNN中使用ReLU的问题并不在反向传播，而是在于正向传播。循环矩阵对正向传播的影响同样是指数级的：对于有界的tanh，这种影响自然被抑制；而ReLU情况下，如果不加限制，输出将指数发散(或衰减)，无法有效学习。但如果循环矩阵是正交矩阵，就不存在该问题了！而且根据之前的分析，这样还同时解决了反向传播的梯度爆炸或消失。
事实上，2015年就有研究尝试对循环矩阵进行合理的初始化及限制，在RNN中使用ReLU：三巨头齐上阵，分别使用单位矩阵(Le et al. 2015)、幺正矩阵(Arjovsky et al. 2015)、正交矩阵(Henaff et al. 2016)进行实现。后续研究(Vorontsov et al. 2017)还发现允许循环矩阵稍微偏离正交(准正交)有助于提升模型效果及收敛速度。最近还有研究尝试将LSTM的门和激活函数也全替换为ReLU (Chandar et al. 2019)，进一步改善梯度消失，效果似乎不错。
而之所以tanh依然在RNN中占据主流，大概是LSTM有效改善了梯度消失问题，因此对引入ReLU的需求也就没那么迫切了。最后，PyTorch中RNN层是提供了tanh与ReLU两个激活函数供选择的，实践中可以都尝试下。

归根结底，RNN的问题根源在于共享循环矩阵，信号被反复放大/缩小，那么问题就来了： RNN为什么要选择不同时刻权值共享？ RNN: a way to share weights over time.
这一问题在花书RNN一章开篇就作了讨论：无论CNN还是RNN，通过权值共享可使模型具有良好的泛化能力，轻松适应不同尺寸/长度的输入。序列数据，如自然语言语句，通常长短不一，如果不同时刻权值不共享，单一模型将很难同时处理不同长度序列，训练集上训练的模型同样很难有效处理测试集数据。又比如，要从语句中提取时间信息，除了句子的长短不一，信息在句子中的位置同样可前可后，并不固定，而如果不同位置(时刻)权值独立，就无法有效提取这一共同信息。
CNN中卷积核可理解为对应特定特征，而权值共享就是扫描该特征，最后通过层层堆叠提取不同(层次)的特征；类似的，RNN就是要在时间维度上扫描特定关联或特征，而这一特征由共享的权值表征，同样可通过RNN单元的堆叠实现对不同(层次)特征的提取。同样是权值共享，两者的核心区别在CNN的特征扫描时的卷积操作间是相互独立的，可直接展开为全连接；而RNN中每步操作则都依赖之前的历史输出，这使得RNN可以提取时序信息，但也使得权值矩阵的影响被指数放大。
虽然权值共享使网络可处理不同长度序列，不过实际训练时，对于长短不一的序列通常还是会通过bucketing & padding进行一定程度的对齐，以提升训练的效率，具体参考这里。

门控记忆单元

在早期(1990年代)，RNN的循环通常要比CNN更深，再加上循环矩阵共享，梯度衰减(及爆炸)问题也更为严重。彼时，ReLU还未被广泛采用，而且即便有ReLU，在RNN中应用也存在问题，这些前面都有讨论。因此，为了解决RNN的梯度消失的问题，人们引入了LSTM，通过“门”控制记忆的留存，为梯度的反向传递引入额外通路。

长短时记忆LSTM：遗忘门、输入门、输出门

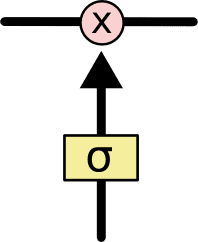
所谓“门”即以下结构，其中 σ 为 Sigmiod 函数，x 为逐元素相乘。Sigmiod 函数的输出位于开区间(0, 1)，从而实现对信息保留比例的控制。

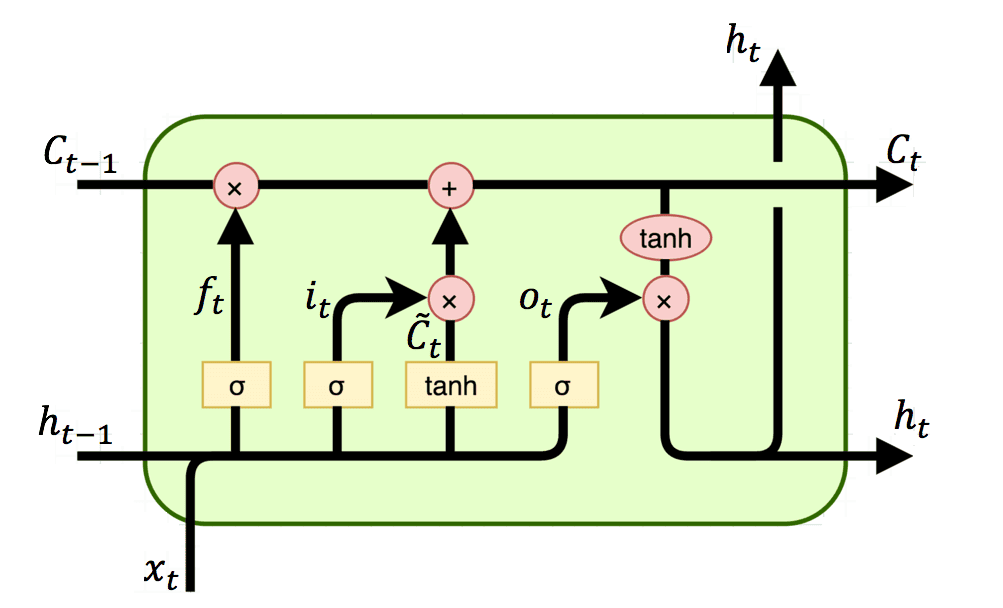
显然上面中的LSTM有三个门，从左至右依次为遗忘门、输入门、输出门。左侧的两个输入，上面对应长期记忆$s_t$，下面对应短期记忆$h_t$。遗忘门根据短期记忆及当前输入决定保留(遗忘)多少长期记忆；类似的，输入门决定多少输入信息可以叠加到内部状态上，输出门决定多少输出信息可以向后传递。

Forward: $\begin{aligned} h_t &= o_t ~ \tanh(s_t)\\ s_t &= f_t ~ s_{t-1} + i_t ~ \tilde{s}_t\\ \tilde{s}_t &= \tanh(W_s \cdot [h_{t-1}, x_t] + b_s)\\ i_t &= \sigma(W_i \cdot [h_{t-1}, x_t] + b_i)\\ f_t &= \sigma(W_f \cdot [h_{t-1}, x_t] + b_f)\\ o_t &= \sigma(W_o \cdot [h_{t-1}, x_t] + b_o)\\ \mathcal{L} &= \sum_{t=1}^\tau\mathcal{L_t} = \sum_{t=1}^\tau\mathcal{L}(h_t) \end{aligned}$
模型参数有输入门的$W_i, b_i$，遗忘门的$W_f, b_f$，输出门的$w_o, b_o$, 更新内部状态的$W_s, b_s$。简单起见，这里先忽略输出门，其余参数以$\theta$表示，对$\theta$求导有：
Backword: $\begin{aligned} \frac{\partial \mathcal{L}}{\partial \theta} &= \sum_{t=1}^\tau \frac{\partial \mathcal{L_t}}{\partial \theta}\\ \frac{\partial \mathcal{L_t}}{\partial \theta} &= \sum_{r=1}^t \frac{\partial \mathcal{L_t}}{\partial h_t} \frac{\partial h_t}{\partial s_t} \frac{\partial s_t}{\partial s_r} \frac{\partial^{+} s_r}{\partial \theta}\\ \frac{\partial s_t}{\partial s_r} &= \prod_{k=r}^{t-1} \frac{\partial s_{k+1}}{\partial s_{k}} = \prod_{k=r}^{t-1} \left[ f_{k+1} + \left( s_k\frac{\partial f_{k+1}}{\partial h_{k}} + \tilde{s}_{k+1}\frac{\partial i_{k+1}}{\partial h_{k}} + i_{k+1}\frac{\partial \tilde{s}_{k+1}}{\partial h_{k}} \right) \frac{\partial h_{k}}{\partial s_{k}}\right]\\ \end{aligned}$
其中$\frac{\partial^{+} s_r}{\partial \theta}$代表不再向$s_{r-1}$, …追溯，$\frac{\partial^{+} s_r}{\partial \theta} = s_{r-1} \frac{\partial f_{r}}{\partial \theta} + \tilde{s}_{r} \frac{\partial i_{r}}{\partial \theta} + i_{r} \frac{\partial \tilde{s}_{r}}{\partial \theta}$。
暂时只考虑$f_{k+1}$一项，因为最终对参数的梯度是所有路径结果之和，对梯度衰减而言，只要有一条路径不衰减，就避免了最终梯度的衰减，这里只分析这条路径中的梯度传播。对比普通RNN，主要区别在于：循环核心由$s_t = Wf(s_{t-1})$变为$s_t = f_t ~ s_{t-1} + i_t ~ \tilde{s}_t$。没有了激活函数，或者说激活函数为恒等映射；循环权重矩阵$W$变为遗忘门值激活值$f_t$，且遗忘门激活值并不会在不同时刻间共享，避免了其影响被循环放大。该路径上最终梯度衰减主要受$\prod_{k=r}^{t-1} f_{k+1}$影响，即由遗忘门激活值$f_t$控制，其取值始终小于1(Sigmoid函数)，因此依然存在梯度衰减问题，但只要控制遗忘门激活值接近1，就可以有效改善梯度衰减。

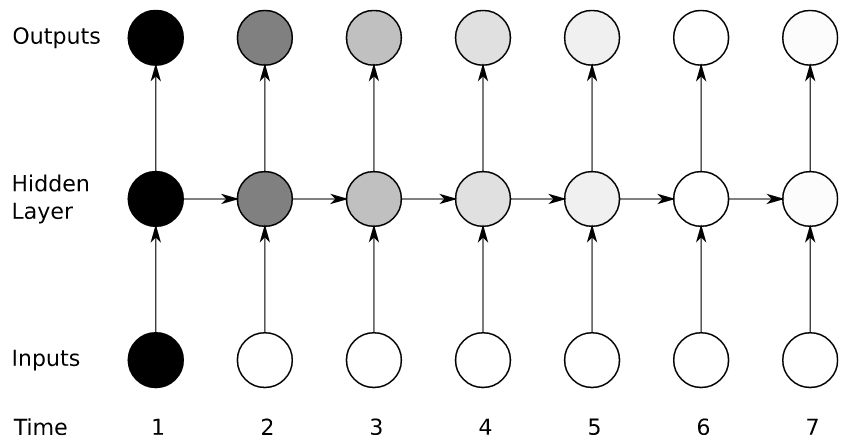
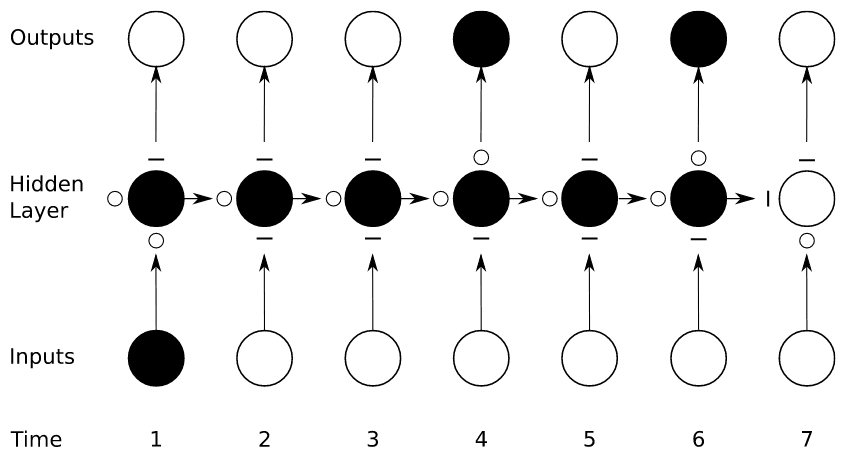
RNN v.s. LSTM：阴影显示了初始输入(t1)的影响力；o/-代表“门”完全打开或关闭

另一方面，对于$\tilde{s}_r, i_r, f_r, o_r$同样是存在循环的：

$$\begin{aligned} \tilde{s}_r ~~ &\xrightarrow{\tanh(W_s \cdot [h_{r-1}, ...])}& h_{r-1}& \xrightarrow{} s_{r-1} \xrightarrow{} \tilde{s}_{r-1} \\ i_r ~~ &\xrightarrow{\sigma(W_i \cdot [h_{r-1}, ...])}& h_{r-1}& \xrightarrow{} s_{r-1} \xrightarrow{} i_{r-1}\\ f_r ~~ &\xrightarrow{\sigma(W_f \cdot [h_{r-1}, ...])}& h_{r-1}& \xrightarrow{} s_{r-1} \xrightarrow{} f_{r-1}\\ o_r ~~ &\xrightarrow{\sigma(W_o \cdot [h_{r-1}, ...])}& h_{r-1}& \xrightarrow{} o_{r-1} \end{aligned}$$

而且这些循环与普通RNN一样，有共享的循环矩阵参与，因此也就存在普通RNN的梯度爆炸和梯度消失问题。如上面所讨论，最终只要有一条路径梯度不衰减，就可以避免整体梯度衰减。而反过来，只要有一条路径梯度发散，整体梯度也将发散。也就是说LSTM可以有效改善梯度消失问题(不能完全避免)，但对于解决梯度爆炸没有帮助。

LSTM是如何缓解梯度消失问题的？
上面已经详细推到并讨论了LSTM对梯度消失的处理，简单概括就是：要避免梯度消失只需要在一条传递路径上梯度不衰减即可，LSTM基于“门”引入了额外的循环回路(长程记忆)，跳过了变换矩阵及激活函数，从而有效缓解了梯度消失，但其余路径依然可能造成梯度爆炸。

门控循环单元GRU：重置门、更新门，将输出门和遗忘门整合为更新门

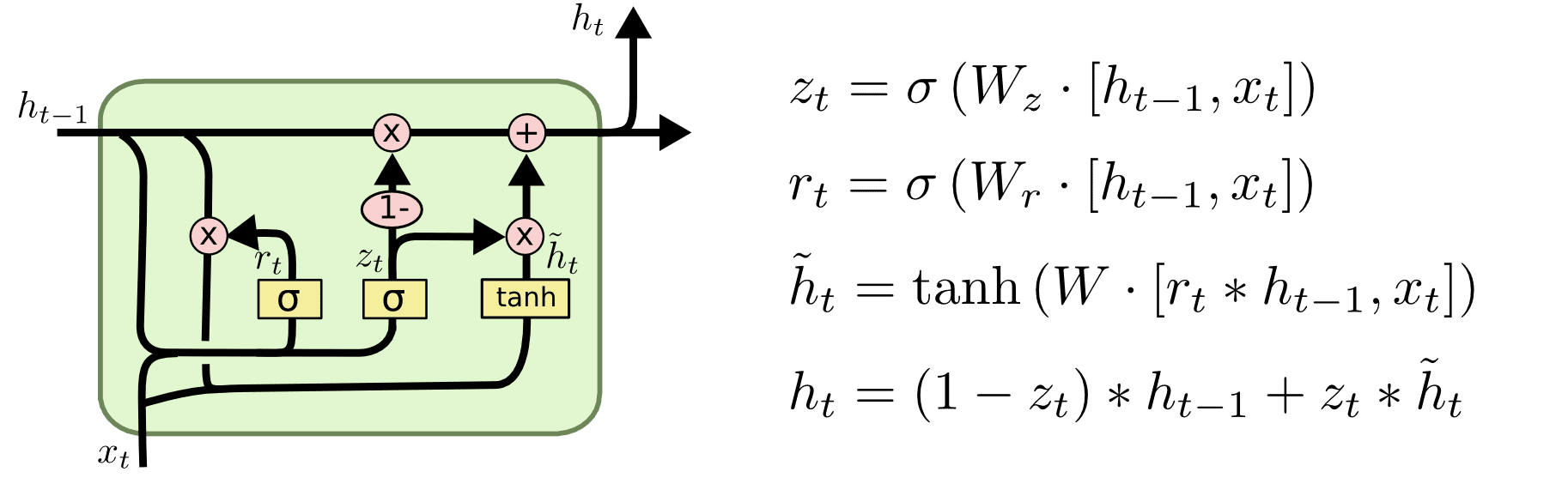
门控循环单元GRU有两个门，分别为重置门和更新门，重置门根据前一刻输出(记忆)及当前输入决定多少记忆可以进入当前单元，而更新门则决定最终输出中历史记忆与当前单元输出各自所占比例。相比LSTM简化了结构，提升了性能。

对称(无向)连接

• 马尔可夫网络(Markov Network)：所有单元之间均可有连接，全部是隐层单元，没有输入输出？
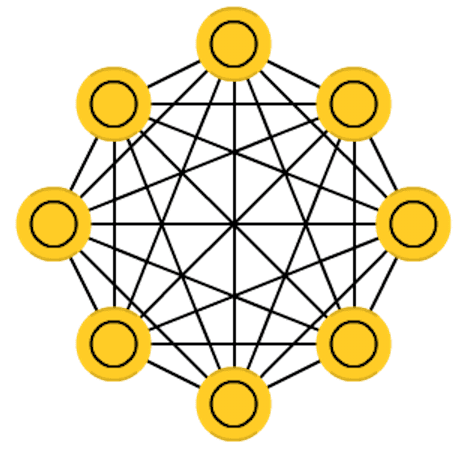
• 霍普菲尔德网络(Hopfield Network)：所有单元之间均可有连接，无隐藏单元，即所有单元都同时负责输入及输出，初始状态对应输入数据，最终状态对应输出，网络更新又分同步与异步两种。
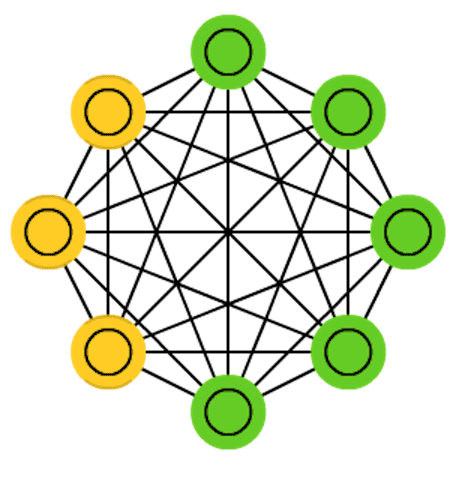
  Hopfield网络中单元节点间权重对称($w_{ij} = w_{ji}$)，与自身连接权重设为0($w_{ii}=0$)，早期激活函数通常取二值函数$s_i =\begin{cases} +1, & \text{if } \sum_j w_{ij} s_j + b_i\\ -1, & \text{ otherwise} \end{cases}$。权重学习规则为$w_{ij} = \frac{1}{N}\sum_k x^{(k)}_i x^{(k)}_j$，其中$k\small\in 1...N$对应不同输入数据。该规则可直观理解为在不通过数据输入中，若两个单元经常同时激活则连接增强；不同时激活，则连接减弱，与赫布(Hebbian)的神经突触连接理论相一致。
• 玻尔兹曼机(Boltzmann Machine)：所有单元之间均可有连接，有隐藏单元(绿色)，即只有部分单元负责输入及输出(黄色)。
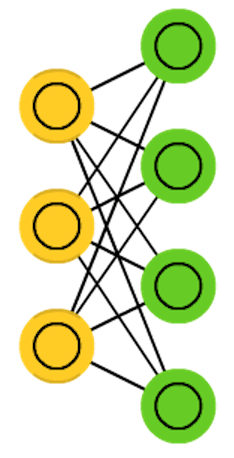
• 受限玻尔兹曼机(Restricted Boltzmann Machine)：分层，层内无连接(受限)，有隐藏层(绿色)，即只有一层负责输入及输出(黄色)。

上文讲述的网络结构(MLP, CNN, RNN)都是分层的、有向的连接，全连接也只是层与层之间的全连接；而这些结构则不分层(RBM除外)，所有单元间均可有连接，且连接是双向(对称)的。这些对称网络与CNN, RNN等都大致起源于同一年代，属于人们在早期对于网络结构的探索(Markov 197x, Hopfield 1982, BM 1985, RBM 1986, RNN 1986/1990, CNN 1989)。在此基础上诞生的深度信念网络(2006)、深度玻尔兹曼机(2009)开启了深度学习的复兴，这些网络对于现在的网络结构设计依然具有参考价值。
虽然多层感知机(MLP)作为前向神经网络最早出现，但或许是因为训练困难未一统江湖，人们依然不断探索其他网络结构。而这些探索的过程却又呈现出某种对称性的破缺：开始的模型最为对称，简洁优美，但功能有限、训练困难；随着针对对称性的限制(受限玻尔兹曼机)，训练变得简单；最终，又回到了最初的有向网络，对称性进一步受限。随着反向传播算法解决了有向网络的训练问题，网络结构逐渐向最初的前馈网络收束。而之后随着算力的突破，模型最终走向了叠加层数提升复杂度的深度网络。

马尔可夫网络、霍普菲尔德网络、玻尔兹曼机、受限玻尔兹曼机

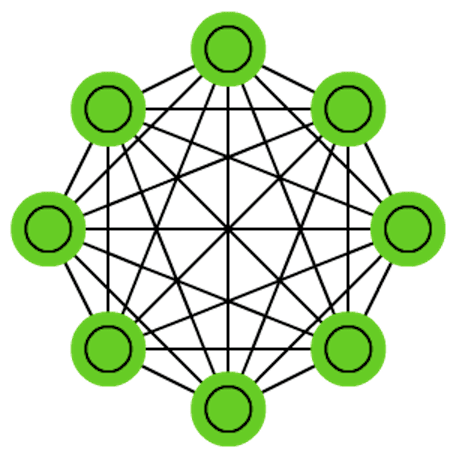
随机失活

Dropout：正则化手段，提升模型泛化能力，避免过拟合

$$y_{\rm train} = \begin{cases} \frac{x}{1-p} &\text{if } u>p \\ 0 &\text{otherwise} \end{cases} \text{Where} ~ u \sim U(0,1)$$

$$E(y_{\rm train}) = p\cdot 0 +(1-p)\frac{E(x)}{1-p} = E(x)$$

注：上述公式中下标train表示Dropout只在训练阶段执行。通过训练阶段神经元的随机失活，相当于训练了很多子网络结构，最终网络对应为所有子网络的集成学习。
*用批归一化后，再用随机失活会导致网络收敛变慢

批归一化

Batch Normalization(2015)

• 逐层尺度归一化(减均值除方差)，避免了梯度消失和梯度溢出；
• 作为一种正则化手段，提升了模型泛化能力，避免过拟合；
• 收敛速度提升5x ~ 20x。

注1：BN在训练阶段是以每个batch的均值方差作为训练集整体均值与方差的估计，而每个batch均值方差都不同，测试阶段所用均值方差是训练阶段各batch均值方差的平均(无偏估计)$E(x) = E_{\mathcal{B}}[\mu_{\mathcal{B}}]; \mathrm{Var}(x) = \frac{m}{m-1}E_{\mathcal{B}}[\sigma^2_{\mathcal{B}}]$，m为batch size。
注2：BN层最初提出时是放在激活函数之前的，有助于缓解tanh或sigmoid造成的梯度衰减，不过最近研究似乎发现放在激活函数之后更合理，尤其是对ReLU而言，具体可参考知乎上的讨论。

Bach Renormalization(2017)

• 训练阶段均值方差引入移动平均的修正；
• 保证了训练和测试阶段的等效性；
• 解决了非独立同分布和mini-batch的问题。

mini-batch的batch比较小，以每个batch的均值和方差作为对整体的估计并不准(波动较大)，batch之间不能保证独立同分布。通过引入移动平均的修正，综合考虑历史batch，有效提升了均值方差估计的稳定性。

批归一化是对神经层中单个神经元(对应下图中通道$\small C$)的所有训练数据(沿数据$\small N$方向)进行归一化，在batchsize很小时效果不好，且对于序列数据，每个批次内数据都长短不一，很难进行合理的归一化。因此对批归一化的后续改进都选择了放弃对批数据的依赖，转而针对单个输入，对神经层内的神经元的数据进行归一化，包括层归一化(LayerNorm)、组归一化(GroupNorm)以及实例归一化(InstanceNorm)。其中层归一化是对单个输入、整层神经元(特征图)进行归一化，组归一是对单个输入、神经元分组归一化，实例归一化则直接对单个输入、单个神经元进行归一化，具体如下图所示。

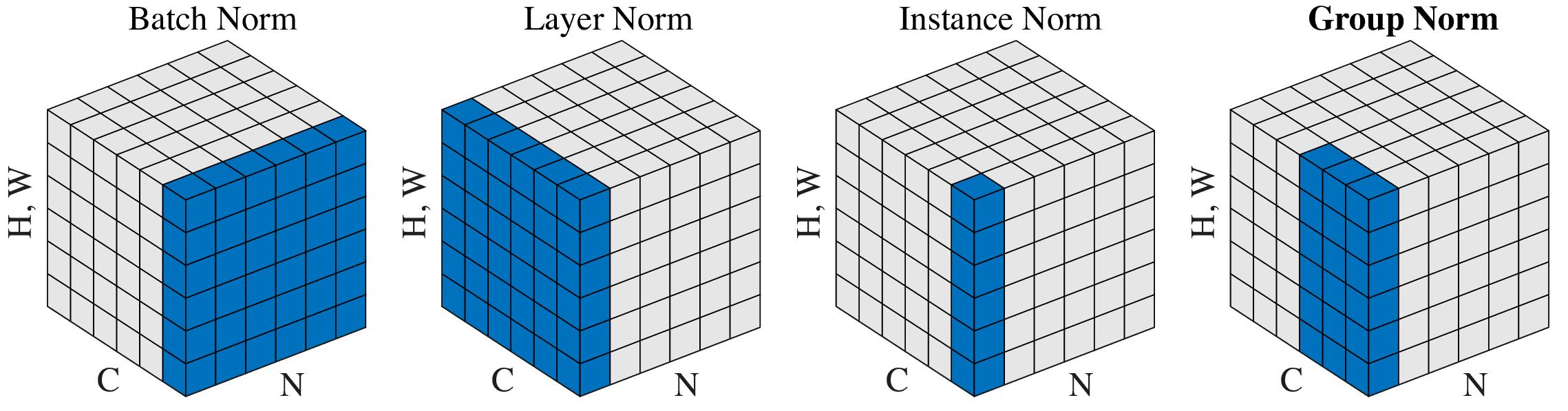
层归一化、实例归一化分属两个极端，而组归一化介于两者之间。层归一化适用于处理序列数据(RNN/LSTM)，实例归一化在处理图片风格转移等强调细节特征的任务时效果较好，而组归一化在batchsize很小时，效果较批归一化更优。

其他单元

激活函数

Sigmoid, tanh, ReLU, Softmax, Maxout, Swish…

• Sigmoid v.s. tanh：tanh(x) = 2σ(2x)-1
  • 两者主要区别在于输出值域，分别为(0,1)与(-1,1)，后者关于0对称(0均值)，可以提升学习的效率，具体参考这篇文章；
  • 此外导数的最大值sigmoid为1/4，tanh为1，前者梯度消失问题更严重；
  • Sigmoid的好处就在于值域为(0,1)，可直接用作概率，常被用于输出层。
• ReLU：Rectified Linear Unit 线性整流函数
  • 导数为1部分有效解决了梯度消失，显著加快深层网络收敛速度；
  • 主要问题在于导数为0的部分可能导致神经元坏死(Dying ReLU)；
  • 此外输出同样非0均值，因此出现了Leaky ReLU, PReLU, ELU等改进。
• Softmax：$\displaystyle {\rm softmax}(x_i) = \frac{e^{x_i}}{\sum_j e^{x_j}}$
  • 输入做指数运算后归一化，输出位于(0,1)，可直接用作概率，可用于输出层；
  • softmax与sigmoid的区别在于，其输出之和为1，适用于单标签多分类问题；
  • softmax是argmax的soft版，后者可直接给出分类，但无法用于梯度反向传递；
  • 指数运算在指数很小(负)或很大时都容易溢出，通常与交叉熵损失融合在一起。
• Softmax：$\displaystyle {\rm softmax}(\beta x_i) = \frac{e^{\beta x_i}}{\sum_j e^{\beta x_j}}$ 或 $\displaystyle {\rm softmax}(x_i/\tau) = \frac{e^{x_i/\tau}}{\sum_j e^{x_j/\tau}}$
  • softmax是argmax的soft版，解决了后者不可微，无法用于梯度优化的问题；
  • 但很多时候我们想要的更多是argmax，softmax的结果可能显得过于soft了；
  • 为此可以引入额外的$\beta/\tau$参数控制soft程度，可视为完全体的softargmax；
  • $\beta$→$\infty$将增强最大值权重，整体输出趋向One-hot编码，而$\beta$→0则趋向平权；
  • soft(arg)max其实源于统计物理Gibbs分布(也称Boltzmann分布)：平衡态系统(温度T)各能态$\epsilon_i$粒子分布服从$p_i = \frac{e^{-\epsilon_i/kT}}{\sum_j e^{-\epsilon_j/kT}}$，其中$\frac{1}{kT}$就对应上面的$\beta$或$1/\tau$，因此$\tau$也被称为温度参数，而$\beta$被称为冷度(coldness)。唯一区别在于指数上多了负号，对应于低能态概率更大，与激活时值越大概率越大相对。
  • 最后，跳出$e$指数限制可能更好理解，将$e^\beta$整体视为$x$指数函数的底数$\frac{b^{x_i}}{\sum_j b^{x_j}}$，则如果$b$取1，则无论数值大小概率均匀分布；$b\in(0,1)$则会放大较小值的概率，随着$b$接近0，函数近似于argmin；$b\in(0,\infty)$则会放大较大值的概率，随着$b$接近$\infty$，函数近似于argmax。
• Maxout：$\displaystyle h_i = \max_{j \in [1,k]}z_{ij}; ~ z_{ij} = x^T W_{... ij} + b_{ij}, W\in \R^{n \times m \times k}, b\in \R^{m\times k}$
  
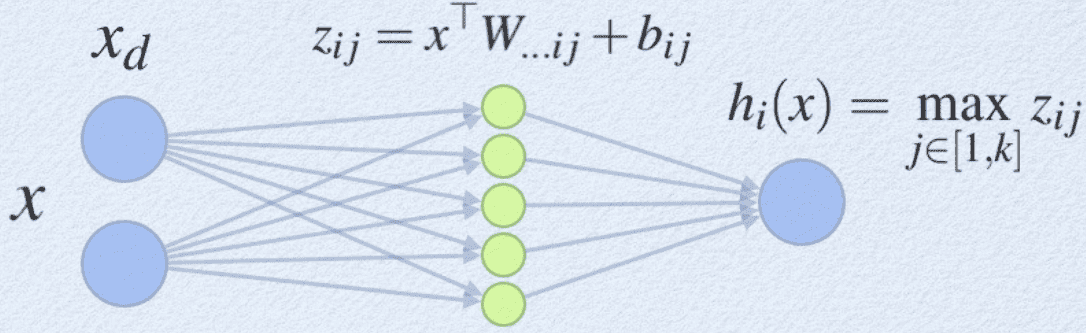
  • 插入一个隐藏层作激活函数，结果相当于一个分段线性函数；
  • 该网络层神经元个数$k$为可调的超参数，权重及偏置参数则由学习调整；
  • 通过学习得到的分段线性函数理论上可逼近任何凸函数，因此非常灵活；
  • 每个maxout层额外引入了$(n+1)\times m\times k$个参数，参数量及计算量大。
• Swish：xσ(βx)

为什么常用的激活函数都是单调的？
万能逼近定理(Hornik et al. 1989, 1990, 1991)对激活函数的要求只是有界和非常数，对连续性、单调性、凸性等没有要求。当然实际应用中，不同函数表现有好有坏，之所以常见激活函数都单调增，只能说是经验：长期实践发现一些比另一些更好，并没有明确原因。
实际上早期有研究(Sopena et al. 1999)发现周期性的正弦函数训练起来比Sigmoid快的多。还有研究(Harmon & Klabjan 2017)尝试将各种激活函数rescale后线性组合，让网络自动学习组合系数，从而对激活函数做出选择，最终发现大多数情况下还是ReLU更有优势。而最近的研究(Ramachandran et al. 2017)对各种激活函数做了一遍暴力搜索，最后发现表现好的也并非都是单调的，准周期性的表现也不错，具体的：

• 表现好的激活函数都相对简单，通常只有1-2个核心单元；
• 准周期性函数其实表现非常不错，如 $\cos(x)-x$ 及 $\min\{x, \sin(x)\}$；
• 包含除法的激活函数，分母需要不为0或分母趋向0时分子也趋向0，以免出现发散；
• 表现好的激活函数，通常有单独的(raw)输入$x$以$+, -, \times, \max, \min$形式参与其中，如$x+\mathrm{sinc}(x), \cos(x)-x, x\cdot\sigma(\beta x), \max\{x, \sigma(x)\}, \min\{x, \sin(x)\}$等，换句话说虽然激活函数需要是非线性的，但表现好的其实都在向线性靠拢，或许是因为这样更易于优化。
• ReLU属于第一梯队，但最好的是$x\cdot\sigma(\beta x)$，更详细讨论可以阅读原文。

损失函数

• Softmax+交叉熵 torch.nn.CrossEntropyLoss

$$\begin{aligned} & \mathcal{L} = -\sum_{n=1}^N \ln(\hat{p}_{n,k_n}), ~~~~~~~~~ \hat{p}_{n,k} = \frac{e^{x_{n,k}}}{\sum_{j=0}^{K-1} e^{x_{n,j}}}\\ & \Rightarrow \mathcal{L}(x) = -\sum_{n=1}^N \left[x_{n,k_n} - \ln\left(\sum_{j=1}^{K} e^{x_{n,j}}\right)\right] \end{aligned}$$

其中$k_n$为当前(第n个)样本的实际分类(总类别数K)，用于单标签多分类问题

交叉熵形式为$H(q,\textcolor{blue}{p}) = -\sum_{x} q(x) \ln \textcolor{blue}{p(x)} = E_q(-\ln \textcolor{blue}{p(x)})$，度量了(预测)分布$p(x)$与(真实)分布$q(x)$的偏离程度。单标签分类问题，对每个样本，取$q(x)$为样本标签的独热(One-hot)编码，$p(x)$为预测的标签概率(由Softmax函数计算)，两者相乘后就只剩下样本实际标签所对应的一项 $-\ln(\hat{p}_{n,k_n})$，最后对所有样本求和，即上述表达式。

如果Softmax激活与交叉熵损失分属两层：交叉熵中包含对数运算，求导时出现$1/x$形式，在$x$很小时容易出现溢出；另一方面，Softmax在计算中涉及指数操作，在指数部分较小或较大时都容易溢出。因此通常将两者融合为Softmax交叉熵损失，即按前面表达式中下面一行的形式计算损失及梯度。

Softmax Loss的一些改进：
　　+ Center Loss：$\mathcal{L_C} = -\sum_{n=1}^N \| x_n - c_{k_n}\|^2$, $\mathcal{L} = \mathcal{L_S} + \lambda\mathcal{L_C}$
　　正确分类的同时，各个类别在特征空间中尽可能紧致(样本与类别中心尽量近)
　　+ Focal Loss：$-\sum_{n=1}^N (1-\hat{p}_{n,k_n})^\gamma\ln(\hat{p}_{n,k_n})$
　　通过权重函数降低易分样本对损失的贡献，更多的去关注难分的样本
　　+ Large Margin：正确分类的同时，各类别在特征空间中尽量远(Large Margin)

• Sigmoid+交叉熵 torch.nn.BCEWithLogitsLoss BCE: Binary Cross Entropy

$$\begin{aligned} \mathcal{L}(x) &= -\sum_{n=1}^N \left[p_n\ln(\sigma(x_n)) + (1-p_n)\ln(1-\sigma(x_n))\right]\\ &= -\sum_{n=1}^N p_n x_n - ln(e^{x_n}-1)\\ \mathcal{L}(x) &= -\sum_{n=1}^N \sum_{k=1}^K \left[p_{n,k}\ln(\sigma(x_{n,k})) + (1-p_{n,k})\ln(1-\sigma(x_{n,k}))\right]\\ &= -\sum_{n=1}^N \sum_{k=1}^K p_{n,k} x_{n,k} - ln(e^{x_{n,k}}-1) \end{aligned}$$

$p_n$ 与 $\hat{p}_n$ 分别为样本某个标签的真实概率及预测概率值，可用于单/多标签二分类问题。

Softmax与Sigmoid激活函数的输出都在(0,1)之间，可直接视作概率，很适合配合交叉熵使用，而且如前面所讨论的，为了数值计算的稳定性，通常会将它们融合在一起计算。两者区别在于：Softmax函数所有输出之和为1，因此可以用于代表样本属于同一标签不同分类的概率值，即单标签多分类问题；而Sigmoid的输出则相互独立，因此可用于表示样本属于不同标签各自的概率，即多标签二分类问题。

• 均方误差 torch.nn.MSELoss MSE: Mean Squared Error

$$\mathcal{L} = -\sum_{n=1}^N \| y_n - \hat{y}_n\|^2$$

适用于连续的实值回归，为避免y值过大导致梯度溢出，可配合Sigmoid先做归一化

• 三元组损失 torch.nn.TripletMarginLoss

$$L(x^a, x^b, x^c) = \sum_{n=1}^N \max\{ d(x^a_n, x^b_n)-d(x^a_n, x^c_n) + \alpha, 0\}, ~ d(x_n, y_n) = \|x_n-y_n\|_p$$

优化算法

• BP算法：链式法则 + 计算图(有向无环图)

• 梯度下降：SGD及其改进

  • GD(全部样本，计算慢、内存需求大) → SGD(随机取单个样本，震荡严重) → Mini-batch SGD(折中，取少部分样本，现在说SGD通常默认为Mini-batch SGD)
  • 权重衰减(weight decay)：损失函数中引入L2正则项，对于梯度下降效果是权重更新时有额外衰减项；
  • 动量(Momentum)：以移动平均方式引入历史梯度修正(momentum)，降低 batch 随机性的干扰，使梯度下降更加平稳，加速收敛。
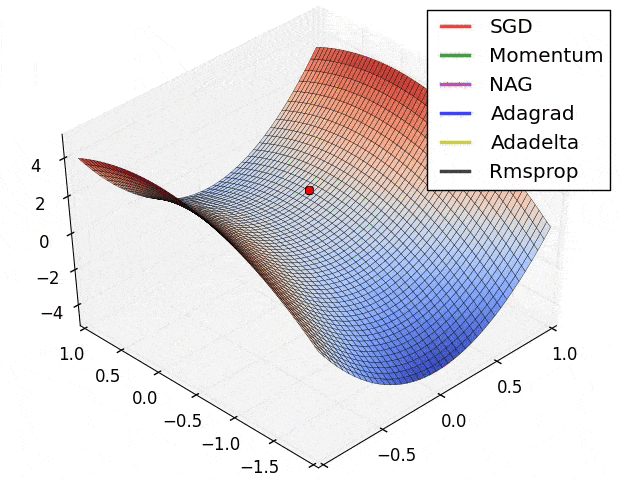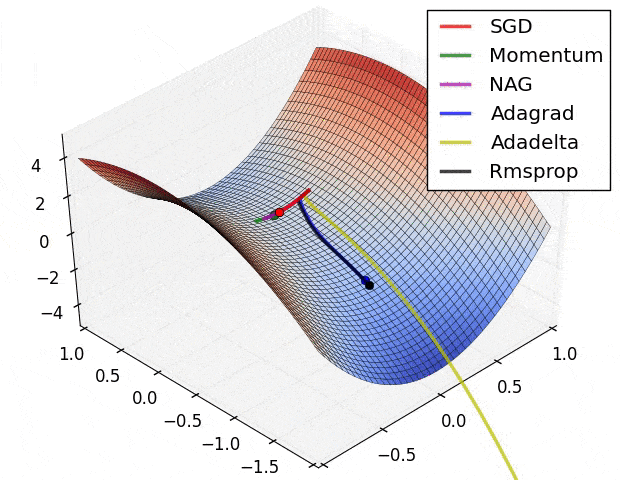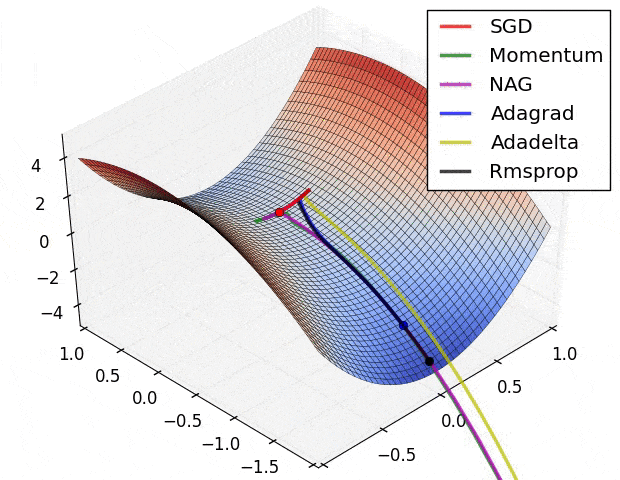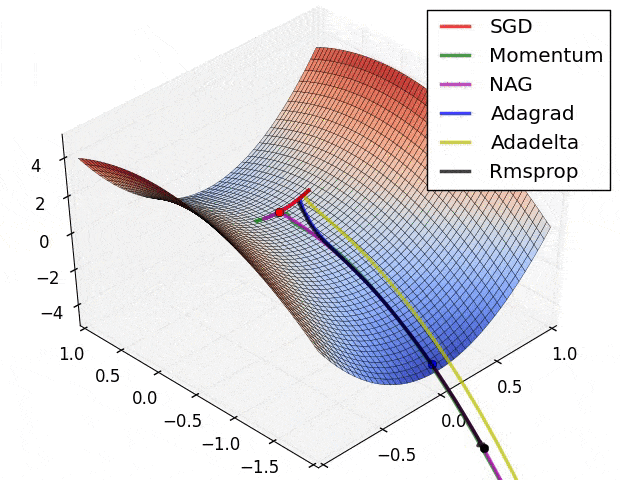
  • SGD改进：Momentum, Nesterov Momentum (NAG), AdaGrad, AdaDelta, RMSProp, Adam, …
    详细对比可参考Sebastian Ruder对优化算法的综述
    
    

    
    SGD改进算法对比

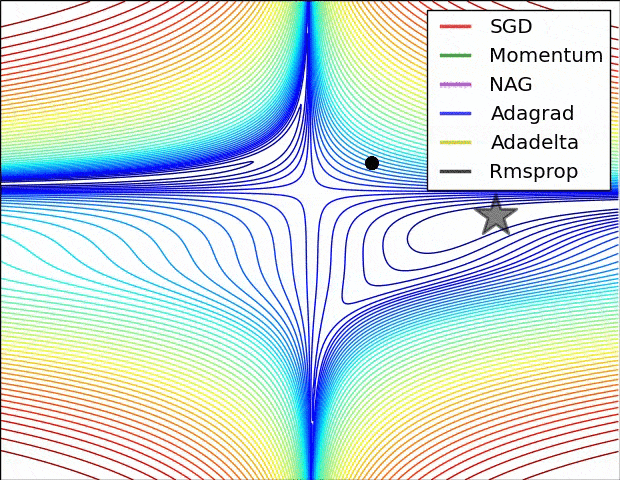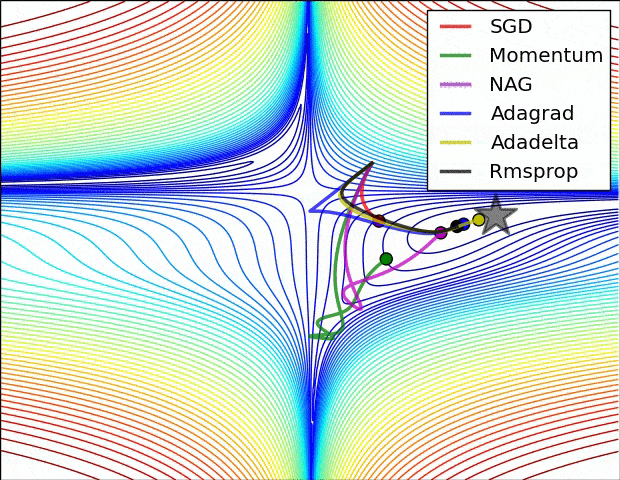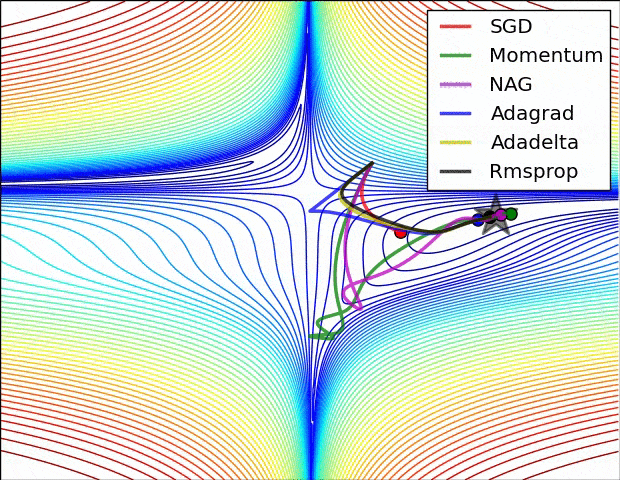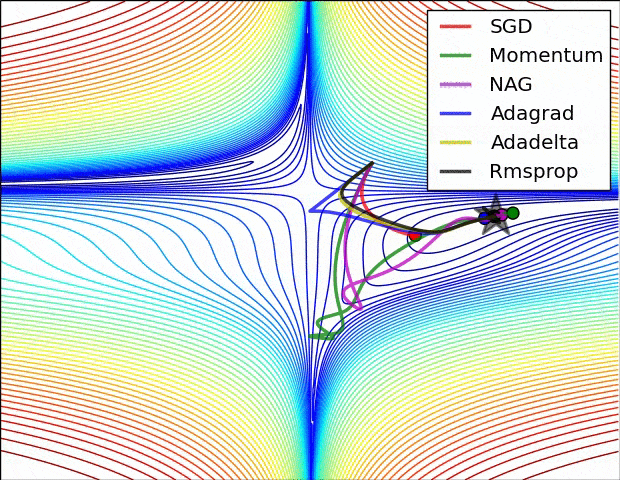
• 学习率：Learning Rate Policy
  按一定策略衰减： Step, Polynomial, Exponential, …

• 未来方向：Learning to Learn(Meta Learning)
  Learning to learn by gradient descent by gradient descent

梯度问题

• 梯度消失
  • 更好的激活函数 ReLU
  • 更好的网络结构 LSTM
  • 数据归一化 Batch Normalization
  • 网络中引入梯度传递的捷径(Skip Connections)
    GoogLeNet(中间层引入辅助损失函数)、Highway(数据分流，一部分走捷径)、ResNet(恒等连接)、DenseNet(每层跟后面的所有层都有连接)

• 梯度爆炸
  • 参数尺度不平衡 -> 合理的初始化：ReLU用MSRA初始化, tanh用xavier初始化
  • 对网络权重引入L1, L2正则项
  • 梯度裁剪

网络捷径

• Highway Layer: $h = t \circ f(Wx+b) + (1-t) \circ x$，其中$t$为门结构类似GRU中的$t = \sigma(W_1x+b_1)$
• Residual connection: $h = f(Wx+b) + x$ 去掉了门结构，直接与上一层间建立捷径
• Dense connection: $h^l = f(W[x^1;...;x^l]+b)$ [;]代表拼接，与之前所有层之间建立捷径

CNN演化

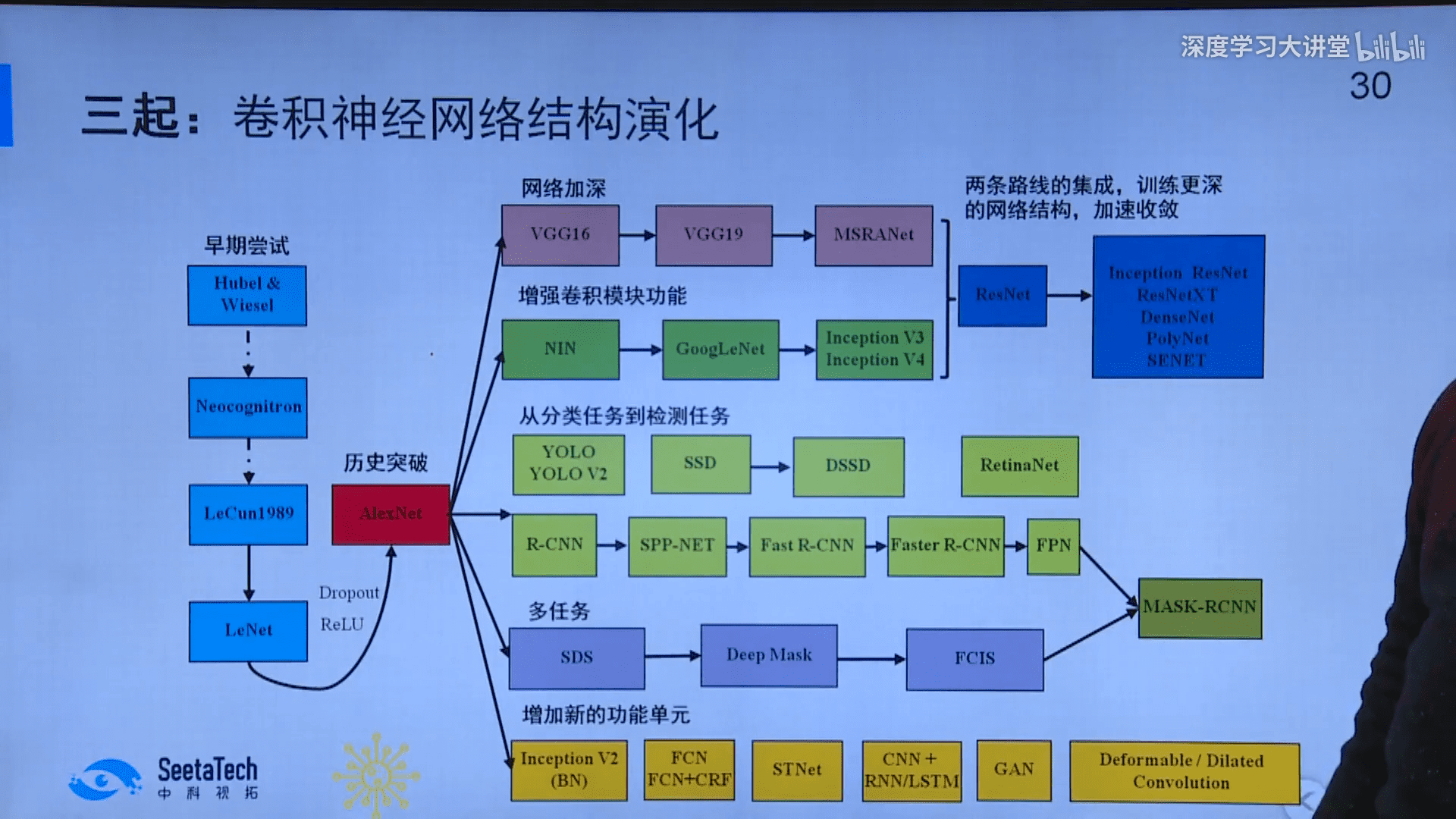纵向加深核心是引入数据传输的捷径，改善梯度衰减；横向扩展主要是子结构(Inception)、分组卷积以及深度可分离卷积；功能创新带来了生成对抗GAN以及自回归AR等无监督生成模型；检测分割则是在分类主干网络上进行功能扩展，有相对独立的脉络。

早期尝试

• Habel & Wiesel 1962 视觉皮层 层级结构
  后续研究发现V1的部分细胞感受野与人工设计的图像特征Gabor小波很像
• Neocognitron 1980 福岛邦彦 生物学视觉模型的计算实现 自组织无监督训练
  后续发展：HMAX(Poggio 1999; Serre 2004, 2007)
• LeCun 1989：卷积、激活函数、全连接、损失函数、反向传播
  tanh比sigmoid收敛快、SGD比GD收敛快；
  初始化保持参数尺度一致(Xavier初始化的雏形)；
  均方误差损失前加入了sigmoid，防止梯度溢出。
• LeNet 1998：在当时被人工设计特征(局部特征描述子)SIFT、LBP、HOG压制
• AlexNet 2012：ReLU、随机失活Dropout、数据增强Data Augmentation
  大数据ImageNet、分组卷积、LRN局部响应归一化(被之后的BN取代)

纵向加深

• VGG 2014：减小卷积核及步长，再配合padding，避免尺寸缩减过快
  每两层卷积一层池化(2×2)，尺寸缩减为1/4，同时通道数翻倍以免信息衰减过快
• MSRANet 2015：将5×5卷积核拆解为两个3×3的，增加网络深度同时降低计算量。
• HighWay 2015：参考LSTM，引入门结构，控制数据分流，一部分数据走捷径
• ResNet 2015, 2016：引入恒等映射捷径(Identity Mapping)
  2016年的工作中将加法后的非线性激活移到了加法之前，残差项跨层可加
• DenseNet 2016：任两层间都相连接，改善梯度消失、加快收敛，较ResNet参数少

横向拓展

• NIN 2014：卷积核替换为MLP(MLPConv)；全连接层替换为全局池化
  NIN(Network in Network)首次引入了1×1卷积，后续在 Inception, MobileNet 等中被广泛应用；全局池化(Global Pooling)在后续Inception, ResNet, SENet中都有应用。
• Inception：名字源于电影Inception(盗梦空间)，其中有台词 We need to go deeper!
  • V1 2014(GoogLeNet：多个Inception结构堆叠)
    中间层引入辅助损失函数，缓解梯度消失，用于辅助训练(测试时关闭)；
    Inception结构：将单个卷积横向扩展为不同尺寸卷积核的并联结构，输出的特征图沿深度方向拼接(concat)，再向后传输。换个角度看，相当于将一个大卷积沿通道方向拆解为一系列独立的小卷积，以稀疏连接的形式，在不显著增加计算量的前提下，有效拓展了网络的横向结构，而且不同尺寸的卷积核还可实现不同尺度上的特征提取。这种沿通道方向对卷积进行拆解以降低计算量的思想，在之后的分组卷积以及深度可分离卷积上得到了延续。
    具体的Inception v1结构包含1个1×1卷积、1个池化、1个3×3卷积、1个5×5卷积；而且在3×3, 5×5卷积之前会使用1×1卷积对通道降维，这里其实已经有了深度可分离卷积的雏形。
  • V2/V3 2015：将5×5卷积拆解为两个3×3；BN；将n×n卷积拆解为1×n与n×1
  • V4 2016：继续调整子网络结构；参照ResNet构建了Inception-ResNet
• ResNeXt 2016：ResNet + 分组卷积，据称能提升模型表示力，比加深网络好
• SqueezeNet 2016：引入1×1卷积与1×1卷积+3×3卷积的串联模块，实现参数缩减
• Xception 2016：将Inception模块中的卷积替换为深度可分离卷积
• MobileNet V1 2017, V2 2018, V3 2019：深度可分离卷积
  V2引入了残差模块；分组卷积之前用1×1升维，之后再由1×1降维(后者用线性激活)。
  V3基于NASNet搜索出的MnasNet优化，参考SENet引入SEblock，使用h-Swish；
  此外V3重新引入了5×5卷积，这是经过网络结构搜索(NAS)出来的结果。
• ShuffleNet V1 2017, V2 2018：ResNet + 分组卷积 + 通道混洗(重新分组)
  V2则从实际实现(内存访问开销)出发，优化网络结构，如控制分组、拼接取代求和等
• SENet 2017：ResNet/Inception + 压缩激励模块(SEblock)
  压缩激励模块：通过全局池化压缩输入通道，再由一个MLP(FC+ReLU+FC+Sigmoid)将其转化为权重，对输入通道进行加权，可理解为一种通道的自注意机制。
• CondenseNet 2017：DenseNet + 分组卷积 + 基于迭代剪枝学习分组
• SKNet 2019：对多个不同感受野(空洞卷积)的分支进行融合，融合时采用类似SENet的机制赋予分支不同权重(逐通道的)，实现感受野的自动调节。

功能创新

• CNN + RNN/LSTM(似乎没什么有影响力的模型)
  CNN特征提取+RNN生成文字描述或完成对话问答；RNN特征提取(视频)+CNN分类
• 生成对抗GAN(Generative Adversarial Network, 2014)
  生成器(反卷积)+判别器(卷积)；提供了对收敛性的理论证明
  应用：数据增强、用GAN的损失作为网络损失的正则项
• 空间变换STN(Spatial Transformer Network, 2015)
  引入空间变换子网络，专用于估计图像仿射变换参数，自动完成图像矫正/对齐。
• 数据归一(Normalization: Batch 2015, Layer 2016, Instance 2016, Group 2018)
• 扩张卷积(Dilated Convolution, 2015) 也被称为空洞卷积、膨胀卷积
  在参数量不变的情况下，不借助池化获得更大感受野，更常见于分割任务
  
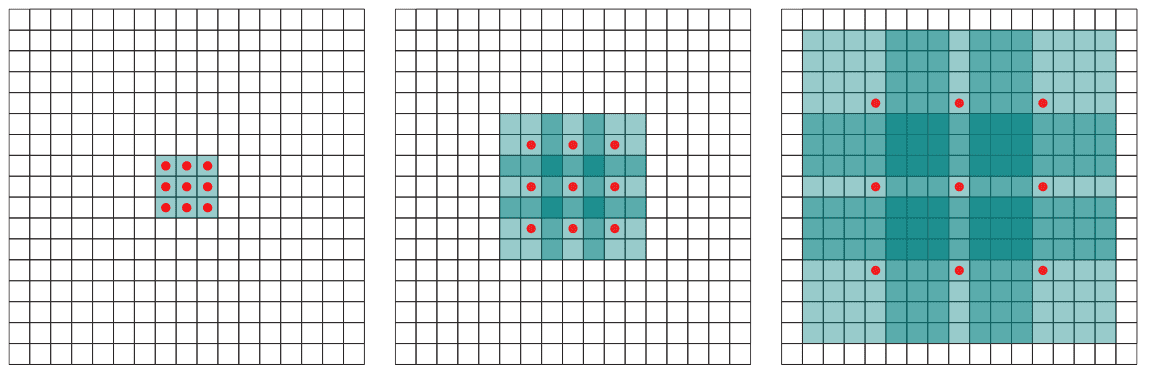
• 自回归AR(Autoregressive)
  神经网络中基于自回归的无监督学习最早可追溯到Hention与Bengio的早期工作，之后在NADE 2011、Sutskeveret al. 2011/Graves 2013??(RNN)、Gregor 2013以及PixelCNN 2016(CNN)等工作中有所发展，并最终被WaveNet, Transformer等发扬广大。
• 扩张因果卷积(Dilated Causal Convolution, 2016)
  WaveNet首次引入因果卷积，并与扩张卷积结合，用于实现自回归，之后被用于时序卷积网络(TCN)及TrellisNet中。所谓因果卷积就是计算t时刻输出时，仅对前一层t时刻以及之前时刻状态进行卷积，确保未来的信息不会泄露到过去。通过多层因果卷积网络叠加，高层的感受野随网络层数线性增加，从而捕获长距离信息。不过，这也意味要获取足够长的历史，网络必须很深，为解决该问题，WaveNet将因果卷积与扩张卷积集合，在保持参数不变同时，通过间隔采样使得感受野随层数增加指数级扩大。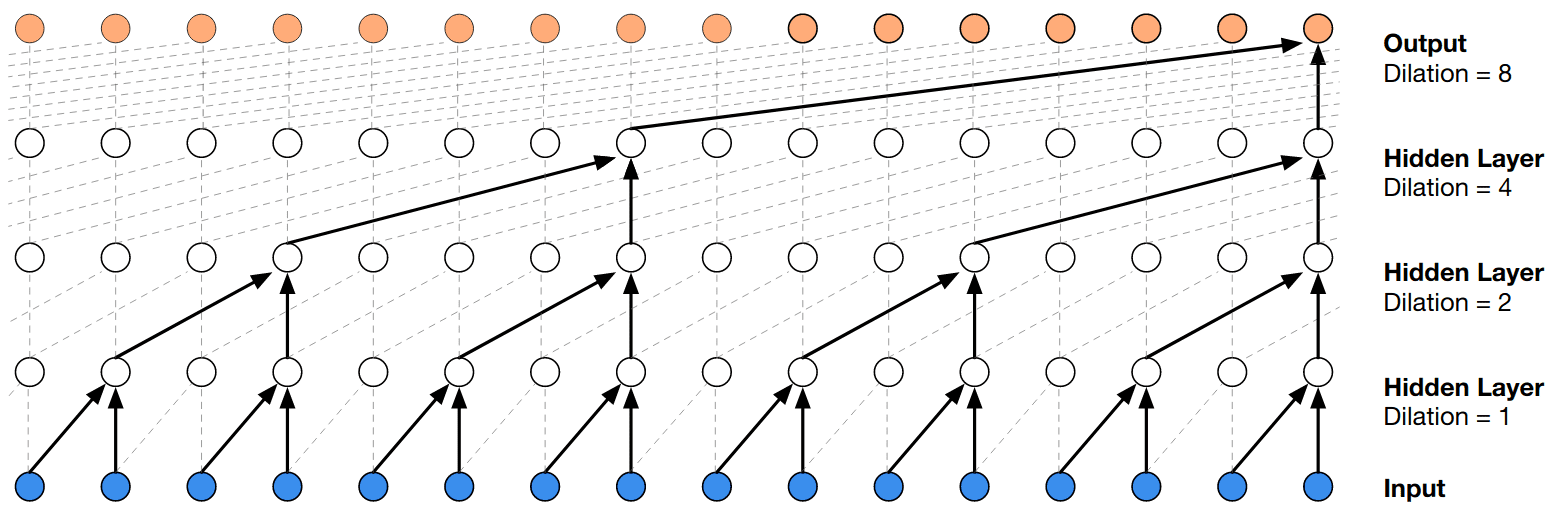
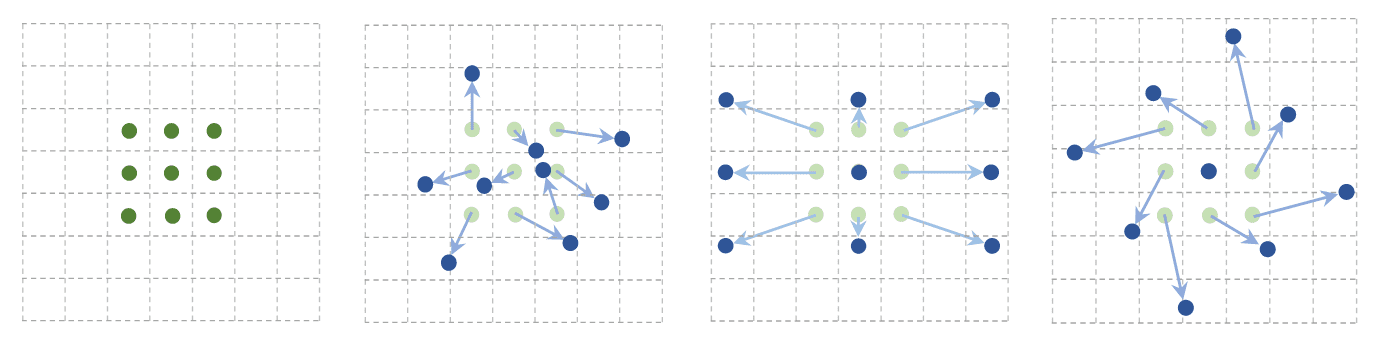
• 可变形卷积(Deformable Convolution, 2017, 2018)
  卷积核及ROI(Region of Interest)可变形，更好的处理有空间形变的视觉任务
  
• 非局部操作(Non-local Neural Network, 2017)
  引入非局域操作，用于捕获时间、空间或时空的长程依赖，适合于视频任务
• 结构搜索NASNet(Neural Architecture Search Network, 2016, 2017)
  用强化学习RL搜索网络结构，后续研究扩展到进化算法EA及一些层级搜索算法。基于结构搜索得到的网络有MobileNet V3、EfficientNet(EffNet), v2、RegNet等。
  其中EfficientNet基于结构搜索得出了网络深度、宽度、输入图像分辨率的一系列最佳组合，用于实现网络在不同应用场景下的便捷缩放；RegNet的文章中对整个网络结构空间参数化，找到最优的参数子空间。

检测分割

• 两阶段检测：Region Proposal + Detection(边框回归BBR+分类CLS)
  • R-CNN 2013：Regions with CNN feature，将深度学习应用到目标检测领域
    选择性搜索(Region Proposal) + CNN(特征提取) + SVM(分类)
    缺点：对每个候选区域都单独用CNN提取特征，速度慢；需缓存大量中间特征
  • SPP-Net 2015：空间金字塔池化(Spatial Pyramid Pooling)
    金字塔池化，与滑窗池化相对，无论输入的尺寸始终输出1+4+16=21维特征
    适用于不同尺寸输入图像，且特征具有更好的尺度不变性(防止过拟合)
    整图提取特征，并在候选区域间共享，直接在特征图上找对应位置，显著提速
  • Fast R-CNN 2015：特征提取与分类融合，基于多任务Loss训练，无需缓存特征
  • Faster R-CNN 2015：RPN + Fast R-CNN
    引入用于生成候选框的卷积网络RPN，且与检测网络共享全图特征
  • FPN 2016：特征金字塔网络(Feature Pyramid Network)
    将特征金字塔网络融合到RPN以及Fast R-CNN中
• 单阶段检测：端到端End-to-End，便捷、速度快，但精度上可能不如两阶段
  • YOLO V1 2015, V2 2016, V3 2018, V4 2020, V5 2021：You Only Look Once!
    V1 整图训练，基于网格预测目标边界；速度快，但对小目标/密集目标精度欠佳
  • SSD 2015：Single Shot multibox Detector
    将RPN与分类网络融合；通过多尺度融合、多个不同长宽比预测器提高精度
  • DSSD 2017：Deconvolutional SSD
    通过反卷积增强对小尺度细节信息的提取，进而提升检测的精度
  • RetinaNet 2017：Focal Loss
    损失中引入调节因子，降低易分样本权重，使网络训练时聚焦于困难样本
  • EfficientDet 2019：基于EfficientNet的检测网络
• 语义分割：像素级分类
  • FCN 2014：Fully Convolutional Networks
    通过上采样(反卷积)使输出与输入尺寸一致；用1×1卷积替代全连接
    “全”卷积网络是指全部由卷积实现的网络：网络中只使用(反)卷积层，去掉了通常位于最后、用于分类的全连接，在FCN中全连接被1×1卷积取代。FCN的优势是支持对任意尺寸、长宽比的图像做像素级分类。
  • DeepLab V1 2014, V2 2016, V3 2017, V3+ 2018
    V1 空洞卷积；FCN + 全连接CRF，基于CRF进一步改善分割结果(V3去掉了CRF)
  • U-Net 2015：主要用于医学图像的语义分割
  • V-Net 2016：主要用于3D医学图像的语义分割
  • PSP-Net 2016：Pyramid Scene Parsing Network
• 实例分割：目标检测+对于目标的语义分割
  • SDS 2014：Simultaneous Detection and Segmentation
  • DeepMask 2015：两个网络同时预测目标Mask及判断Mask是否覆盖目标
  • FCIS 2016：Fully Convolutional Instance-aware Semantic Segmentation
    RPN + 分割，同时处理多类实例，类别间会存在竞争
  • Mask R-CNN 2017：Faster R-CNN + FCN
    边框回归 + 分类 + 分割，解决了FCIS类别竞争的问题；RoI Align(线性插值)
  • YOLACT 2019, YOLACT++ 2020：You Only Look At CoefficienTs
  • SOLO V1 2019, V2 2020：Segmenting Objects by Locations
• 全景分割PS：语义分割 + 实例分割
  • Panoptic Segmentation 2018：开山之作
  • EfficientPS 2020：基于EfficientNet的分割网络

扩展阅读

人工智能发展简史 - Aminer
Hinton 与神经网络：从 RBM 到 Capsule
Deep Learning模型发展4条脉络 - 唐杰THU
Backpropagation In Convolutional Neural Networks
A guide to convolution arithmetic for deep learning, github
Deconvolution and Checkerboard Artifacts - distill.pub
The Unreasonable Effectiveness of Recurrent Neural Networks
Understanding LSTM Networks - colah’s blog
Ising 模型，Hopfield 网络和受限的玻尔兹曼机
An overview of gradient descent optimization algorithms
Image Segmentation
Neural Networks, Manifolds, and Topology - colah’s blog
将神经网络理解为仿射变化(线性权重, 偏置)+拓扑变换(非线性激活函数)，空间的维度对应每层的神经元数目，而层数的叠加对应变换的叠加，最终将纠缠的数据变换为线性可分。最理想的情况是数据所在空间不断膨胀，而各个类别本身保持聚集(inflating the space between manifolds for different categories and contracting the individual manfiolds)，这感觉有点类似宇宙膨胀的同时，气体在引力作用下保持聚集(星系)。