DL Specialization

Posted on 2022-02-22 In Learning , MOOC Views: Waline:

Deep Learning Specialization：课程视频、课程主页
新版Coursera免费用户旁听课程不能提交答案了…
吴恩达的厉害之处在于他可以从零出发，越过“知识诅咒”，试图以初学者视角引入必要知识。

https://abdur75648.github.io/Deep-Learning-Specialization-Coursera/

Deep Learning:Theoretical Motivations

AI for Everyone

机器学习与数据科学

机器学习：无需显式编程即可使计算机具备学习能力 - Arthur Samuell (1959)
[流程] 数据收集、模型训练、迭代调优、模型部署、反馈调整 (成果为软件本身)
[实例] 计算广告/推荐系统/自动驾驶/个性化教育/精准农业… <相对标准化>
数据科学：从数据中获取知识或深度见解，最终成果通常是辅助决策的演示文档
[流程] 数据收集、数据分析、猜想检验、提炼建议(文档)、测试反馈(A/B Test)
[实例] 商业分析/客户分析/流程优化… <更具针对性>

人工智能公司

网络公司：A/B测试(更快的更新迭代，小步快跑)、决策下放(给予了解技术/用户的工程师或产品经理自主权)
智能公司：数据平台(策略性数据收集+统一的数据仓库)、高度自动化(自动化程序替代人力)、智能算法应用

拥抱人工智能

从商业价值的核心驱动因素或主要的业务痛点入手
实现具体任务(task)的自动化，而非尝试替代整个工作岗位(job)
技术审视(可行性、数据量、项目时间) + 商业审视(商业价值、财务分析) + 道德审视
拥抱行业标准，将有限的资源聚焦于核心商业价值，而非重复造轮子

NN&DL Theory

理论基础：神经网络、深度网络

价格预测 → 简单线性回归 → 不能取负数 → ReLU(非线性)天然存在
结构化数据(数据表/数据库) v.s. 非结构化数据(图片、文本、语音)

Geoffrey Hinton: (大脑)生理学+物理学 → 哲学 → 心理学 → 木匠 → AI
反向传播算法之前就有人提出但未引起注意，直到Hinton将文章发表在Nature。而为了文章发表，Hinton做了很多社交工作，如私下与潜在审稿人交流沟通。
概念(心理学)：特征集合(特征向量Embedding) ⇄ 结构主义(语义网络)
玻尔兹曼机BM/受限玻尔兹曼机RBM、深度信念网络(RBM+信念网络)、变分贝叶斯

Read the literature, but don’t read too much of it. Trust your intuitions. (Replicate the work instead of just read.) Find Advisor who has belifs similar to yours, and work on stuff that your advisor feel deeply about.

分类问题

二分类 sigmoid

输出： $\hat{y} = w^Tx+b$ 线性回归 → 逻辑回归 $\hat{y} = \sigma(w^Tx+b), \sigma(z) = \frac{1}{1+e^{-z}}$
损失： $\small\displaystyle \mathcal{L}(y, \hat{y}) = - [y\log(\hat{y}) + (1-y)\log(1-\hat{y})]$ 凸函数
代价(总损失)： $\small\displaystyle \mathcal{J}(w, b) = - \frac{1}{m}\sum_{i=1}^m\mathcal{L}(y^{(i)}, \hat{y}^{(i)})$ ( $i$ 指示单个样本)
梯度： $\small\displaystyle \frac{\partial \mathcal{L}}{\partial z} = \hat{y}- y$ （ $\frac{\partial \mathcal{L}}{\partial z} = \frac{\partial \mathcal{L}}{\partial \hat{y}} \frac{\partial \hat{y}}{\partial z}, \frac{\partial \mathcal{L}}{\partial \hat{y}} = -\frac{y}{\hat{y}} + \frac{1-y}{1-\hat{y}}, \frac{\partial \hat{y}}{\partial z} = \hat{y}(1-\hat{y})$ ）
计算图：将计算拆解为基本运算复合 → 导数链式法则 → 计算图求导

矢量化：线性代数(数据的矢量)、向量微积分(Jacobi矩阵、Hessian矩阵)
直观的，可将其理解为数据和对应标签分别存入列表，计算时基于矩阵操作并行计算而非逐个循环。实现上，对于图片数据可展开为一维列向量

x

(n,1)，并将所有训练数据合并为矩阵

X

(n,m)，对应的，数据标签合并为一维行向量

Y

(1,m)。

Z = w^T X + b, \hat{Y} = \sigma(Z)

，这里偏置项

b

为标量，输出

Z

为(1,m)的行向量，涉及广播操作，同时激活函数

\sigma

同样需要是矢量化函数。
建议：在创建“一维”向量时明确用行向量(shape(n,1))或列向量(shape(1,n))，而非一维向量(shape(n,))。其他避免维度问题的技巧：在矩阵求和时keepdims=True，使用assert检查向量维度，使用reshape改变维度，以及为避免切片降维，可使用单元素切片代替单个元素保持维度(如[1:2,:]代替[1,:])，或者使用expand_dims重建维度。

# X: image dataset (N x W x H x C) ->  (N x WHC)
# X_unroll = X.reshape(X.shape[0], -1).T
# X: image dataset (N x W x H x C) ->  (WHC x N)
X_unroll = X.reshape(X.shape[0], -1).T
# image2vec(unroll) -> standardize(preprocessing) -> model: func, init,
# prop(foward:loss, backward:gradient), optim(gradient descent), predict

关于损失函数的理解：最大化给定输入

x

，输出对应为

y

的概率

p(y|x)

。

\hat{y}

取值区间为0到1，且值越大对应于

y

为1的概率越高，因此可将

\hat{y}

理解为

y

取1的概率

p(y=1|x)=\hat{y}

。又

y

只能取0或1，两种情况下

y

取值的概率以乘法形式可合并为

p(y|x) = \hat{y}^{y}(1-\hat{y})^{(1-y)}

(当然有其他写法，如用加法，但无助于理解目标损失)。上述概率的对数取负即为损失函数，而总的损失对应总概率(概率相乘)的负对数。

多分类 sigmoid → softmax

输出： $\small\displaystyle \hat{y}_i = {\rm softmax}(z_i) = \frac{e^{z_i}}{\sum_j e^{z_j}}$ （当分类数为2时就回归了sigmoid）
损失： $\small\displaystyle \mathcal{L}(y, \hat{y}) = - \sum_{i=1}^C y_i\log(\hat{y}_i) = - \log(\hat{y}_k)$ （独热编码 $y$ 只有正确类别 $k$ 项为1）
代价(总损失)： $\small\displaystyle \mathcal{J}(w, b) = \frac{1}{m}\sum_{i=1}^m \mathcal{L}(y^{(i)}, \hat{y}^{(i)})$ （ $i$ 指示单个样本）
梯度： $\small\displaystyle \frac{\partial \mathcal{L}}{\partial z} = \hat{y}- y$ （ $\frac{\partial \mathcal{L}}{\partial z_i} = \frac{\partial \mathcal{L}}{\partial \hat{y}_k} \frac{\partial \hat{y}_k}{\partial z_i}, \frac{\partial \mathcal{L}}{\partial \hat{y}_k} = -\frac{1}{\hat{y}_k}, \frac{\partial \hat{y}_k}{\partial z_i} = \hat{y}_k\delta_{ik} - \hat{y}_k\hat{y}_i$ ）

神经网络

结构：逻辑回归(相当于单个神经元) → 神经网络(神经元层层堆叠) 隐藏层
数学： $z = \bm{w}^Tx+b, ~\hat{y} = a(z)$ 参数矩阵 $\bm{w}$ 的列对应神经元， $b$ 为列向量
　　　 $\mathcal{L}(y, \hat{y}) = -[y^T\log(\hat{y}) + (1-y)^T\log(1-\hat{y})]$

数据矢量化：数据矩阵对应数据逐列排布(列对应样本，行对应特征维度/神经元)
　　

\small Z = \bm{w}^TX+b, \hat{Y} = a(Z); \mathcal{J}(\bm{w}, b) = -\rm{tr}[Y^T\log(\hat{Y}) + (1-Y)^T\log(1-\hat{Y})]

上面讨论中，参数矩阵

\bm{w}

由各神经元参数作为列向量拼接而成，另一种常见表达是将神经元参数作为行向量拼接，此时

\bm{w}

无需再转置，

z = \bm{w}x+b

。
数据矩阵

X

也可表示为样本逐行排布，pandas数据表就默认以行为样本索引，列为特征索引；TensorFlow/Pytorch中也选择用第一个维度(最左侧)表示数据的batchsize，即(batchsize, data_shape)，可理解为数据样本按行排布。这其实是很自然的选择，将数据样本以Python列表存储，样本指标自然对应首维。对于数据逐行排布情况，对应

Z

也按行排布，

b

为行向量，则有

\small Z = X \bm{w}+b

，其中

\bm{w}

为逐列排布的参数矩阵。不过因为单个数据作为列向量的理解更普遍，因此前面的表达更常见。

import tensorflow as tf
(mnist_train, _), _ = tf.keras.datasets.mnist.load_data()
print(mnist_train.shape, mnist_train[0])
# mnist_train为(60000, 28, 28)的ndarray，后两维度对应图像矩阵
(imdb_train, _), _ = tf.keras.datasets.imdb.load_data()
print(imdb_train.shape, imdb_train[0])
# imdb_train为(25000, )的ndarray，元素为列表(序列单词索引)
# 由于序列长度不等，x_train元素为(列表)对象，而非数组

from torchvision.datasets import MNIST
mnist_dataset = MNIST(download=True)
print(len(mnist_dataset), mnist_dataset.data.shap())
# mnist_dataset为元素数60000的DataSet对象
# 其data属性为(60000, 28, 28)的Tensor类型

from torchtext.datasets import IMDB
imdb_iter_train, imdb_iter_test = IMDB()
print(len(imdb_iter_train), next(imdb_iter_train))
# imdb_iter_train为元素数25000的可迭代Dataset对象

激活：sigmoid(通常只用于输出层), tanh(比sigmoid更优), ReLU(最推荐)/Leaky ReLU
梯度： $\sigma'(x) = \sigma(x)(1-\sigma(x))$ , 　 $\tanh'(x) = 1-[\tanh(x)]^2$
　　　 $\frac{\partial \mathcal{J}}{\partial z^{[L]}} = \hat{Y}- Y, \frac{\partial \mathcal{J}}{\partial z^{[l]}}= \bm{w}^{[l+1]} \frac{\partial \mathcal{J}}{\partial z^{[l+1]}} \circ a'$ ( $\circ$ 为逐元素相乘)
　　　 $\frac{\partial \mathcal{J}}{\partial \bm{w}^{[l]}}= \frac{1}{m} A^{[l-1]} \frac{\partial \mathcal{J}}{\partial \bm{z}^{[l]}}^T,\frac{\partial \mathcal{J}}{\partial b^{[l]}}= \frac{1}{m} \text{sum}(\frac{\partial \mathcal{J}}{\partial z^{[l]}}, \text{axis}=1)$
初始化：全0初始化，不同神经元完全相同或者说完全对称，经过迭代后也将继续保持对称。而为了使不同神经元实现不同功能(提取不同特征)，我们需要对神经网络进行随机初始化(偏置参数 $b$ 可初始化为0)。此外，初始化参数通常取为接近0的小值(如取均值为0，方差0.01)，以使 $z$ 也保持接近0，从而避免使用sigmoid或tanh激活函数时过快出现梯度消失，降低学习效率。如果完全未使用饱和激活函数，则问题不大。

深度网络

数学： $\small Z^{[l]} = w^{[l]}F^{[l-1]} + b^{[l]}, F^{[l]} = a^{[l]}(Z^{[l]})$
其中 $l$ 为层数， $a^{[l]}$ 为激活函数， $F^{[l]}$ 为各层输出(特征向量)， $F^{[0]}$ 对应数据输入。
每层网络将特征维度由 $n^{[l-1]}$ 变为 $n^{[l]}$ ，基于向量乘法，参数 $w^{[l]}$ 维度为 $(n^{[l]}, n^{[l-1]})$
数据矢量化并不影响网络参数维度( $b$ 需要广播)，但 $z, f$ 由列向量扩展为矩阵 $Z, F$ 。
深度：直观上浅层网络提取局域特征，如边缘/线条检测，深层网络对浅层网络提取的特征逐级整合，越深层的网络视野越广，对应更全局的特征。另一方面，根据万能逼近定理，浅层网络已经够用，但粗略来讲用浅层网络替代深层网络近似一些函数时，所需隐含层节点数将指数级增加。比如 $x_1$ xor $x_1$ … xor $x_n$ 的电路开关状态，可由深度为O(logn)的树结构网络表示，总开关数为O(n)，而若用单隐含层的网络，所需开关数将为O(2ⁿ)。对应到神经网络，假设目标问题有 $n$ 个特征 $x_i, i \in (1, ..., n)$ ，每个特征有 $m$ 个状态，则系统整体有 $m^n$ 个可能状态，单隐层的网络理论上需要O(mⁿ)的参数用于逐个判断(维度灾难)，而如果将特征在二叉树中分散组合，则只需要深度O(logn)的树结构，总节点数O(n)/参数量O(mn)。用浅层网络得不偿失，增加深度可显著减少宽度。最后，针对某些具体问题可能并不需要深度网络，可从最简单的逻辑回归开始，以层度作为超参数，多做些尝试，搜索最佳选择。
实现：[正向]逐层计算 $z^{[l]}$ 及激活后的特征 $f^{[l]}$ 直至损失函数，(缓存 $z^{[l]}$ 用于梯度计算)
　　　[反向]从损失开始，逐层向前计算 $dw^{[l]}, db^{[l]}, dz^{[l]}, df^{[l-1]}$
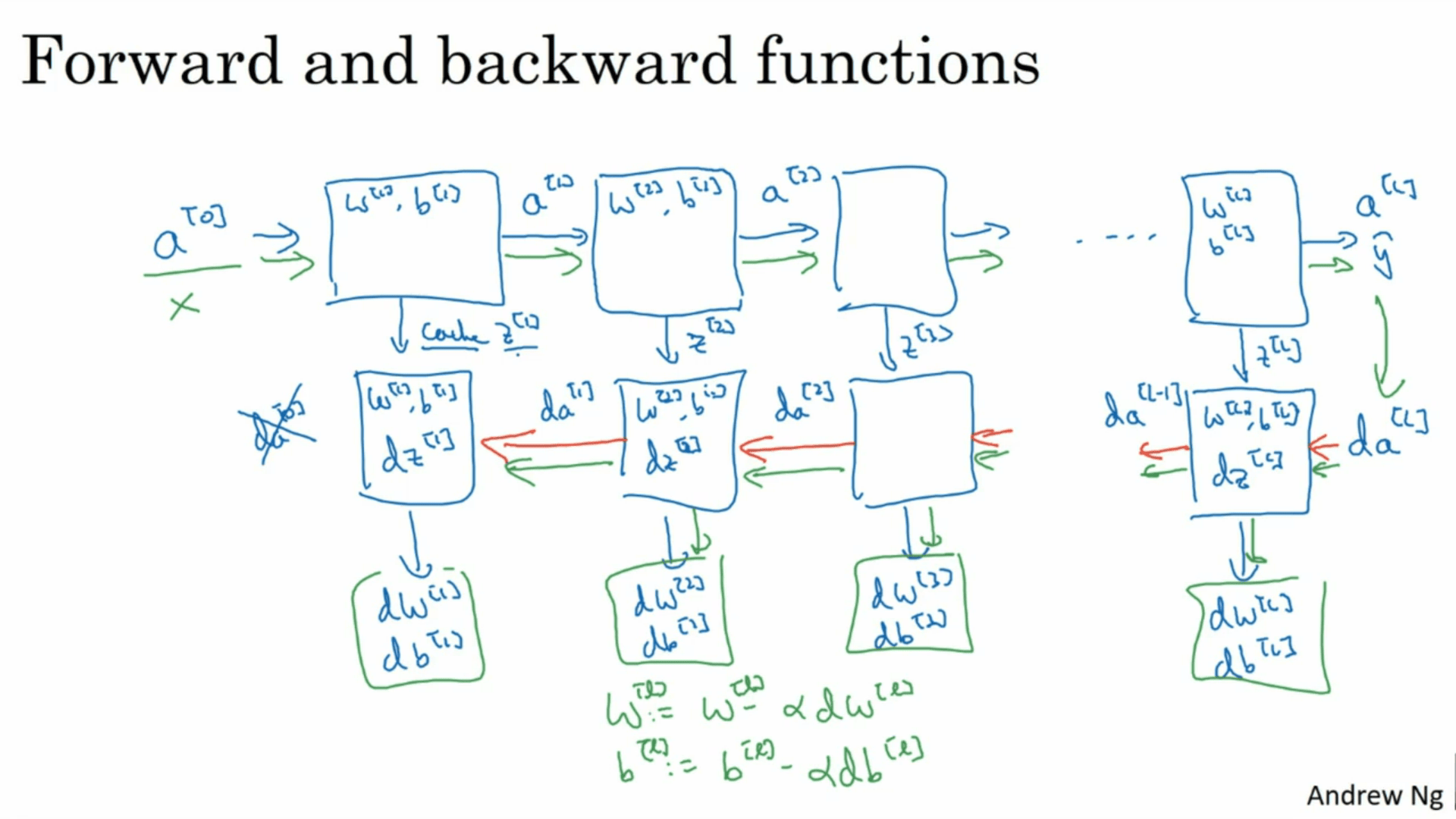
超参数：学习率、训练迭代次数、层数、各层单元数、激活函数、动量项、分批大小、正则化参数

具体实例
优化指定的损失函数：optimizer.minimize(loss, var_list, tape=None)
其中loss参数可以是数值或函数：loss是值(tensor)时，需配合tape参数一起使用；loss是函数(callable)时，返回值为损失，且不能有任何参数。

import tensorflow as tf

w = tf.Variable(0.) # w = tf.Variable(0, dtype=tf.float32)
optimizer = tf.keras.optimizers.Adam(0.1)

def loss_fn()
      cost = w**2 - 10*w + 25 # w是全局变量，无需作为参数
    return cost

def train_step():
    optimizer.minimize(loss_fn, var_list=[w])

print(w)
for step in range(300):
    train_step()
print(w)

线性回归

import tensorflow as tf
import matplotlib.pyplot as plt

n_samples = 100
tf.random.set_seed(42)
x = tf.linspace([0.], [1.], n_samples)
rng = tf.random.Generator.from_seed(42)
err = rng.normal(shape=(n_samples, 1))*0.1
y = 10*x + err

model = tf.keras.Sequential([
          tf.keras.layers.Dense(1, input_shape=(1,))  # w*x+b
          ])

optimizer = tf.keras.optimizers.Adam(0.1)
model.compile(optimizer=optimizer, loss='mse')
history = model.fit(x, y, epochs=100, verbose=0)
# plt.plot(history.history['loss'])

plt.scatter(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.plot(x, model(x), 'r')
w, b = model.weights
plt.title(f'y = {w[0][0]:0.2f} x + {b[0]:0.2f}')
plt.show()

上述compile和fit过程，使用tf.GradientTape可展开为以下过程：

optimizer = tf.keras.optimizers.Adam(1)

model = tf.keras.Sequential([
          tf.keras.layers.Dense(1, input_shape=(1,))  # w*x+b
          ])

def train_step(x, y, model):
    with tf.GradientTape() as tape:
        y_predict = model(x)
        loss = tf.reduce_mean((y-y_predict)**2)
    optimizer.minimize(loss=loss, var_list=model.trainable_weights, tape=tape)
    return loss

epochs = 100
loss = []
print(model.layers[0].get_weights())
for epoch in range(epochs):
    training_loss = train_step(x, y, model)
    loss.append(training_loss)
print(model.layers[0].get_weights())

注意，模型训练时，网络权重、学习率等信息会保持记录，再次训练时将在之前基础上继续，没有简单的重置方法。这里相对简单，直接重新搭建模型，而为确保可重复性更好的做法是保存最初训练前的初始权重，需要重置时载入权重。

进一步的，可使用Numpy完全手动实现自动微分(这里线性回归使用2维数据)，最易出错的地方是参数梯度的维度：

import numpy as np
import plotly.express as px
import plotly.figure_factory as ff
from scipy.spatial import Delaunay

n_samples = 100
rng = np.random.default_rng(seed=42)

X_train = rng.uniform(0., 1., size=(n_samples, 2)) # shape=(batchsize, ndim)
w_mock = np.array([[10.], [2.]])                   # shape=(ndim, 1)
err = rng.normal(0, 0.1, (n_samples, 1))
Y_train = X_train@w_mock + err                     # shape=(batchsize, 1)

# weight initialization
def initializing_weight(dim):
    w = np.zeros((dim, 1))
    b = 0
    return w, b

#forward & backward
def propagate(w, b, X, Y):
    # forward
    Y_pred = X@w + b
    loss = np.mean((Y-Y_pred)**2)
    
    # backward
    dw = X.T @ (-2*(Y-Y_pred)/X.shape[0])
    # dw = -2*np.mean(X * (Y-Y_pred), axis=0, keepdims=1).T
    db = -2*np.mean(Y-Y_pred)
    grads = {"dw": dw,
             "db": db}
    return grads, loss

# optimize
def optimize(w, b, X, Y, epochs, learning_rate):
    losses = []
    for epoch in range(epochs):
        grads, loss = propagate(w, b, X, Y)
        losses.append(loss)
        dw, db = grads['dw'], grads['db']

        w = w - learning_rate*dw
        b = b - learning_rate*db
    
    params = {"w": w,
              "b": b}
    return params, losses

# metrics
def metrics(w, b, X, Y):
    Y_pred = X@w + b
    mape = np.mean( np.abs(Y-Y_pred)/Y )
    print(f"mean absolute percentage error:{mape:.5f}")

def plot_data(w, b, X, Y):
    tri = Delaunay(X)
    simplices = tri.simplices
    fig = ff.create_trisurf(X[:,0], X[:,1], (X@w + b)[:,0], simplices=simplices)
    fig.add_scatter3d(x=X[:,0], y=X[:,1], z=Y[:,0], mode='markers')
    fig.updatl(layout_title=f'y = [{w[0][0]:0.2f}, {w[1][0]:0.2f}] x + {b:0.2f}')
    return fig

def fit(X, Y, epochs, learning_rate, show_loss=True, 
        show_metrics=True, show_data=False):
    w, b = initializing_weight(X.shape[1])
    params, losses = optimize(w, b, X, Y, epochs, learning_rate)
    w, b = params['w'], params['b']

    if show_loss:
      fig = px.line(x=np.arange(epochs), y=losses, log_y=True)
      fig.show()
    if show_metrics:
      metrics(w, b, X, Y)
    if show_data:
      fig = plot_data(w, b, X, Y)
      fig.show()

fit(X_train, Y_train, 200, 0.3, show_data=True)

这里使用矩阵相乘(y = x@w + b)，y为标量，使用元素相乘则y为矢量，梯度计算是相同的，只需上述代码中数据生成及前向传播部分变为元素相乘(y = x × w.T + b)即可处理。

上面的手动微分处理的是
二分类问题

from sklearn import datasets
X, Y = datasets.make_classification(n_samples=1000, n_features=2, random_state=42,
                          n_redundant=0, n_informative=1, n_clusters_per_class=1)
X_train = X
Y_train = Y.reshape((-1,1))

# utils function
def sigmoid(z):
    s = 1/(1+np.exp(-z))   
    return s

# forward & backward
def propagate(w, b, X, Y):
    # forward
    Y_pred = sigmoid(X@w + b)
    loss = np.mean(((- np.log(Y_pred))*Y + (-np.log(1-Y_pred))*(1-Y)))
    
    # backward
    dy = (Y_pred-Y)/X.shape[0]
    dw = X.T @ dy
    db = dy.sum()
    grads = {"dw": dw,
             "db": db}
    return grads, loss

# metrics
def metrics(w, b, X, Y):
    Y_pred = sigmoid(X@w + b)
    Y_label_pred = (Y_pred >= 0.5) * 1

    accuracy = 1 - np.mean(np.abs(Y_label_pred - Y))
    print(f"train accuracy: {accuracy*100:.2f} %")

def plot_data(w, b, X, Y):
    fig = px.scatter(x=X[:,0], y=X[:,1], color=Y[:,0].astype(str))
    
    x = np.linspace(-0.2, 0.1, 100)
    fig.add_scatter(x=x, y=-(w[0,0]*x+b)/w[1,0], mode='lines', name='boundary')
    #sklearn.inspection.DecisionBoundaryDisplay
    return fig

fit(X_train, Y_train, 200, 0.1, show_data=True)

多分类问题

from sklearn import datasets
from sklearn.preprocessing import OneHotEncoder
from sklearn.metrics import classification_report, confusion_matrix, roc_auc_score
digits = datasets.load_digits()
data_X = digits.images
data_Y = digits.target

X_train = data_X.reshape((data_X.shape[0], -1))
Y_train = OneHotEncoder(sparse=False).fit_transform(data_Y[:,None])

# utils function
def softmax(z):
    s = np.exp(z)/np.exp(z).sum(axis=1, keepdims=True)
    return s

# forward & backward
def propagate(w, b, X, Y):
    # forward
    Y_pred = softmax(X@w + b)
    loss = np.mean(- Y * np.log(Y_pred))
    
    # backward
    dw = X.T @ (Y_pred-Y)/X.shape[0]
    db = np.mean(Y_pred-Y)

    grads = {"dw": dw,
             "db": db}
    return grads, loss

def metrics(w, b, X, Y):
    Y_pred = softmax(X@w + b)
    Y_labels_pred = np.argmax(Y_pred, axis=1)
    Y_labels = np.argmax(Y, axis=1)

    auc = roc_auc_score(Y_labels, Y_pred, multi_class='ovr')
    print(f"roc_auc_score:{auc}")

    report = classification_report(Y_labels, Y_labels_pred)
    print(report)

    report_matrix = confusion_matrix(Y_labels, Y_labels_pred)
    fig = px.imshow(report_matrix, text_auto=True)
    fig.show()

fit(X_train, Y_train, 200, 0.1, show_data=False)

Engineering

工程实践：初始化、正则化、归一化、优化策略、超参数调试

实践要点

数据划分：训练集(train)、验证集(valid)/开发集(dev)、测试集(test)
验证集用于模型(超参数)的评估及筛选，测试集用于检验最终模型效果，因此数量上只要能达到相应目的即可，而训练集则通常多多益善。中小数据集(~万)，经验选择为60/20/20或70/30；超大数据集(~百万)，验证、测试集可能取1%即可，即98/1/1。通常随数据量增加，验证、测试集占比可适当降低。
通常深度学习训练所需数据量巨大，因此可适当放宽对训练数据的要求，但至少应尽量确保验证集数据分布与最终应用场景(测试集)保持一致。验证集由于参与模型的迭代调整，并不能代替测试集提供模型效果的独立无偏估计。不过在一些没有测试集的情况，也会有人用“测试集”指代验证集，理解即可，本质上这种表述并不准确。
偏差与方差：通过训练集、验证集的预测误差评估模型预测的偏差和方差。训练集误差反映了模型对数据的拟合程度，即预测的偏差；验证集误差反映了模型对于训练数据之外数据的适应性(泛化能力)，即预测的方差。(以人类误差为基准)
偏差与方差的应对策略不同，偏差可通过的扩充网络(增加层或每层单元)、增加训练迭代或改善优化策略以及切换更合适的网络结构改善；方差可通过扩充数据、正则化以及切换更合适的网络结构改善。基本做法是先考虑训练集预测精度，将偏差降至合理范围后，再去考虑降低方差，之后再回头再降偏差，如此循环迭代，直至偏差与方差都降至可接受范围。
正则化：L2正则、L1正则 (矩阵的L2范数也被称为Frobenius范数)
理论上，L1正则有助于模型参数稀疏化，但Andrew Ng认为实践上效果不明显
L2正则相当于参数(权重)更新时在参数前乘以小于1的因子，也被称为权重衰减
随机失活(Dropout)：输出特征矩阵与随机概率判断矩阵逐元素相乘
[Inverted Dropout] 计算各层输出时要除以留存率，以使输出值期望保持不变。
注意，在计算验证、测试集时应关闭随机失活，将整个训练网络用于预测(基本等效于随机失活+多次平均)。上面随机失活时的翻转操作确保了关闭随机失活后，模型输出结果与预期保持一致，而无需额外缩放。
[直觉理解]随机失活后实际使用了更小的网络进行训练，减少过拟合的可能，且在某种程度上可理解为众多小网络的集成学习，提升了整体结果鲁棒性。从另一角度，随机失活避免了对特定特征(节点)的过度依赖(co-adaptation)，从而使模型参数更平均的分散在所有节点，降低单个节点的权重(不会出现特定节点权重特别高)，效果上类似L2正则。
此外，不同隐藏层随机失活概率可以不同，网络参数多的层(更易过拟合)可设置更低的留存率，而参数较少的层则可以完全不失活，甚至输入层也可设置随机失活(但通常不这样做或至少取较大留存率)。这样的缺点是引入很多需要调节的超参数，一种折中做法是，在保持单一留存率的同时，设置某些层不参与随机失活。
Andrew Ng 的建议是如果模型没有过拟合，就先不要用随机失活。在机器视觉领域，由于输入维度很大，网络参数超多，数据量通常是不足的，很容易过拟合，所以在机器视觉领域随机失活几乎是默认选择，但本质上它是防止过拟合的手段(正则化)。
随机失活的最大缺点是损失函数不再有明确定义(每次都随机变动)，因此无法绘制损失函数随训练迭代的降低情况，用于调试分析。只能将留存率取1，确定一切正常，再开启随机失活并期待一切依然保持正常。
更多正则化：数据增强(翻转/旋转)、提前终止迭代
提前终止是寻找偏差与方差之间的平衡，但对于深度学习，偏差与方差的应对策略不同，更好的做法是交替的逐个优化(正交化策略)，提前终止会使两者耦合而无法单独优化。Andrew Ng 更倾向于使用L2正则而非提前终止，交替优化偏差与方差，缺点是需要多次尝试正则参数 $\lambda$ ，计算量会更大。
数据归一化：减均值除方差 (验证、测试集归一化时需使用训练集的均值和方差！！)
不同特征梯度下降正比于其激活值，使特征取值处于同一量级(几何上避免损失函数出现狭长等高线)，有助于提升训练时SGD的稳定性，加快优化速度。
网络初始化：避免过快出现网络梯度的爆炸或消失
考虑最简单的线性激活并忽略偏置(此时梯度就是参数矩阵的乘积)，随着网络层数增加，输出很容易出现指数级放大(矩阵特征值大于1)或衰减(矩阵特征值小于1)。
在sigmoid激活函数神经网络中， $\frac{\partial \mathcal{L}}{\partial z^{[l]}} = w^{[l+1]T}\frac{\partial \mathcal{L}}{\partial z^{[l+1]}}\circ\sigma'(z^{[l]})$ ，同时存在激活函数导数的连乘和权重矩阵的连乘，从而导致梯度爆炸或消失。
初始化基本经验是保持输出与输入特征在同一量级，由 $z=wx$ 随着输入 $x$ 的特征维度 $n$ 增加， $w$ 取值要减小~ $\frac{1}{n}$ 。由于 $w$ 通常在0附近随机初始化，经验法则是取 $w$ 的方差为 $\frac{1}{n}$ (即典型值为 $\small \pm\sqrt{\frac{1}{n}}$ 之间)，对于ReLU激活函数 $\frac{2}{n}$ 效果更好：
$\sigma_{w^{[l]}} = \sqrt{\frac{1}{n^{[l-1]}}}$ (tanh)、 $\sigma_{w^{[l]}} = \sqrt{\frac{2}{n^{[l-1]}}}$ (ReLU)、 $\sigma_{w^{[l]}} = \sqrt{\frac{2}{n^{[l-1]}+n^{[l]}}}$ (Xavier init)
Understanding the difficulty of training deep feedforward neural networks
文中取 $w$ 在0附近均匀分布而非正态分布 (深度前馈网络与Xavier初始化原理)

梯度检查：[数值近似]单侧差分近似误差为O(ε)量级，双侧差分近似误差为O(ε²)量级
将网络的全部参数展开拼接为一个列向量，对参数逐一计算梯度的双侧差分近似；网络自动微分得到的参数梯度也做相应展开拼接，检查两者差别 $\frac{\|d\Theta_{\rm approx} - d\Theta\|_2}{\|d\Theta_{\rm approx}\|_2 + \|d\Theta\|_2}$ $\frac{∥ d Θ _{a p p r o x} - d Θ ∥ _{2}}{∥ d Θ _{a p p r o x} ∥ _{2} + ∥ d Θ ∥ _{2}}$ 。取ε为10^-7，如果上述偏差~10^-7则可接受，如果~10^-5则存疑，如果~10^-3则很可能网络实现存在错误。
注意，这里需要对网络的所有参数逐个进行计算，计算量还是相对较大的，因为数值近似每次只能对单个变量进行计算。花书给的一个建议是对输入输出做变换，定义 $f(x) = \bm{u}^Tg(\bm{v}x)$ $f (x) = u^{T} g (v x)$ ，这里 $x$ $x$ 是标量， $\bm{u}, \bm{v}$ $u, v$ 为矢量，通过变换矢量函数变为标量函数，从而用单变量的数值梯度进行验证。函数 $f$ $f$ 的梯度计算依赖于 $g$ $g$ 的梯度，通过随机选取几组 $\bm{u}, \bm{v}$ $u, v$ 可确认 $g$ $g$ 梯度的正确性，具体可参考Deep learning。
Tensorflow和Pytorch等框架都提供了专门的梯度检查函数(tf.test.compute_gradient, torch.autograd.gradcheck)。基于框架内置算符构建网络时计算图会自动记录，梯度基本不会有问题。梯度检查在自定义算符时需要重视。
- 只在调试时运行梯度检查，训练时记得关闭，以免拖慢速度；
- 梯度差别较大时，确定引起差别的具体参数，以定位问题位置；
- 不要遗漏正则项，同时关闭随机失活(确定损失较为复杂)；
- 除了训练起始进行梯度检验，可在训练一段时间后再次核对，以免错误被接近0的初始参数所掩盖。

优化策略

小批量GD：在梯度下降时一个极端是每次选择单个样本计算，逐个遍历数据(随机梯度下降SGD)，而考虑到数据矢量化可加快计算，另一个极端是单次利用所有数据样本计算(全批量梯度下降BGD)。但当数据量过大(~百万)，单次处理超大矩阵很耗内存，也会拖慢计算。因此通常做法是两者折中，将数据分批(单批~百)，逐批的遍历数据，被称为小批量梯度下降(Mini-batch GD)。小批量梯度下降相比SGD充分利用了数据矢量化的提速；相比BGD会引入一定随机性，但减少了单次梯度下降的计算压力，同样可有效提升训练速度。
- 如果数据量不大(数千量级)，直接全批量梯度下降BGD
- 对超大数据集，batchsize通常取64, 128, 256, 512等(2的指数)
- 确保GPU/CPU的内存容量可容纳单批次数据(否则将严重拖慢速度)
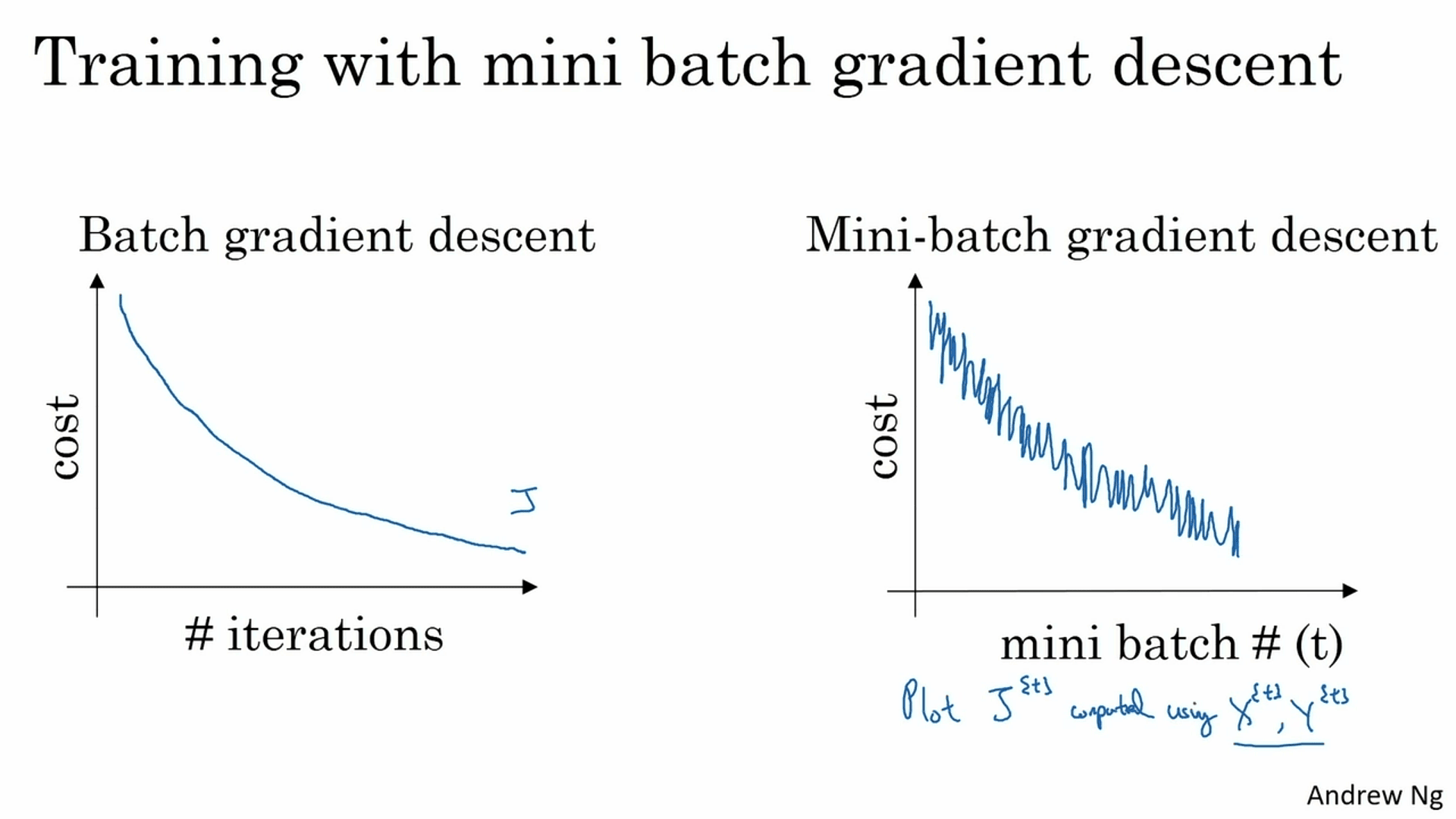
指数加权平均： $v_{t} = \beta v_{t-1} + (1-\beta)\theta_t$
将上述关系展开 $v_{t} = (1-\beta)\theta_t + (1-\beta) \beta \theta_{t-1} + (1-\beta) \beta^2 \theta_{t-2} + ...$
对小量 $\epsilon\sim 0$ 有 $\ln(1+\epsilon)\sim\epsilon, (1-\epsilon)^{\frac{1}{\epsilon}}\sim \frac{1}{e}$ , 因此 $\beta\sim1$ 时， $\beta^{\frac{1}{1-\beta}}\sim \frac{1}{e}$ ，即每过 $\frac{1}{1-\beta}$ 个 $\theta_t$ 项，式中 $\beta$ 的指数项将带来 $1/e$ 的衰减。如果忽略这之后的项，同时忽略 $\frac{1}{1-\beta}$ 项之内的 $\beta$ 指数衰减， $v_{t}$ 就近似于 $\frac{1}{1-\beta}$ 个 $\theta_t$ 项的移动平均，且通过 $\beta$ 参数可调节移动平均的窗口大小， $\beta$ 越大滑动窗口越大，结果越平滑。不过相对于简单的移动平均，这里存在一个 $\beta$ 的指数衰减项，压低距离当前 $\theta_t$ 更远的 $\theta$ 项的权重( $\small \beta\lesssim1$ )，所以是指数加权(移动)平均。相比普通移动平均，优势在于基于递推关系只需当前 $\theta_t$ 及前一项 $v_{t-1}$ 即可得到 $v_{t}$ ，无需存储所有平均相关项，降低了存储及单次计算成本。
[偏置修正]指数加权平均中通常取 $v_0=0$ ，这会使起始的 $\frac{1}{1-\beta}$ 项相比正常平均存在明显偏置，可通过除以 $1-\beta^t$ 项加以修正( $v_1=\theta_1$ )，不过深度学习中通常不必要。
动量梯度下降： $dw \rightarrow v_{dw} = \beta v_{dw} +(1-\beta)dw$ 　　经验值 $\beta\sim0.9$
在对批次迭代时，将当前梯度替换为指数加权平均，用于梯度下降。通过移动平均，可一定程度上降低小批量梯度下降的随机性。在物理近似上，可将原梯度项 $dw$ 视为变速项，而 $v_{dw}$ 可视为速度累积后的动量项，通过引入累积的动量减少了单次变速的影响，使运动整体趋势更平稳。而从计算角度，移动平均相当于隐式扩大了所使用的batch size，从而降低单个batch随机性的干扰，使梯度下降更加平稳，加速收敛。
最后，也有使用 $v_{dw} = \beta v_{dw} + dw$ 形式的表达，相当于将 $1-\beta$ 项吸纳进了梯度更新时的学习率参数 $\alpha$ ，缺点是超参调优时改变 $\beta$ 可能就需要相应改变 $\alpha$ 。
$\beta=0$ 关闭动量项，值越大越平滑，通常取0.8到0.999，0.9为相对合理的默认选择。
均方根传播(RMSprop)： $dw \rightarrow \frac{dw}{\sqrt{S_{dw}} + \epsilon}, S_{dw} = \beta S_{dw} +(1-\beta)dw^2$ (逐元素平方)
对导数的平方进行指数加权平均，开根号后(均方根)用于对导数进行缩放，使不同参数的梯度相对均衡，从而缓解特定方向上的震荡。
适应性矩估计(Adam)： $dw \rightarrow \frac{v_{dw}/(1-\beta_1^t)}{\sqrt{S_{dw}/(1-\beta_2^t)} + \epsilon}$ (动量 $v_{dw}$ + 均方根 $\sqrt{S_{dw}}$ 调节)
$v_{dw} = \beta_1 v_{dw} +(1-\beta_1)dw, S_{dw} = \beta_2 S_{dw} +(1-\beta_2)dw^2$
参数经验取值： $\beta_1\sim0.9, \beta_2\sim0.999, \epsilon\sim 10^{-8}$ ，学习率 $\alpha$ 仍需调节
注意Adam的效果体现为损失更快的减少收敛，而非更平滑的损失曲线
学习率衰减：指数衰减、固定步长衰减等 $\frac{1}{1+r*n_{\rm epoch}}, r^{n_{\rm epoch}}, \frac{k}{\sqrt{n_{\rm epoch}}}, ...$
学习率本身的确定比选择衰减策略优先级更高
基于Transformer的大模型通常训练更困难，学习率最开始通常不会取很大，但太小又训练缓慢。常见做法是从接近0开始，随着训练线性上升(warm-up)，再平滑衰减(如指数函数、cos函数)，比如Transformer论文中就采用了前4000步线性上升，随后指数衰减的策略。
局部最优解：低维空间的直觉可能并不适用于高维空间，在高维空间中梯度为零处更可能是鞍点而非局部最优。其逻辑为在梯度为零的局域，函数沿各维度方向均可表现为凸或凹，而局部最优要求所有维度方向都为凸函数。随着空间维度增加，满足该条件的概率也将随之显著降低，更可能的情况是在某些方向上为凸，另一些方向上为凹，即表现为鞍点。因此问题并不在于陷入局部最优，而在于导数接近零的平台区会拖慢梯度下降的速度，而前面讲的优化策略有助于改善该问题。更数学的，还可从Hessian矩阵来理解，局部最优要求Hessian矩阵为正定矩阵，即矩阵所有特征值大于0，而特征值数等于参数维度，随着维数增加，全部为正的概率也将随之减小。

超参调优

超参调优：经验直觉要不断修正，随数据或算力更新每隔几个月应重新评估
- 优先级：Andrew Ng对超参数划分了大致优先级，但哪个影响大还是靠实验
  学习率；动量项 $\beta$ (如果是Adam则通常不调整)、批次大小(batchsize)、隐层单元数；网络层数、学习率衰减策略
- 搜索策略：随机采样而非网络搜索 + 由粗到细
  同样的实验次数，随机采样相比网络搜索，对每个参数都提供了更多采样，从而更快定位最优参数区域；其次在定位最优参数区域后，可对该局域进行更精细采样(由粗到细)。
- 采样技巧：线性尺度均匀 v.s. 对数尺度均匀(跨越不同量级，放大0附近取值)
  某些超参数如隐层单元数或网络层数等，均匀采样是不错选择；而学习率对0附近的变化更敏感，动量项 $\beta$ 对1附近的变化更敏感。因此对于学习率而言更合适的是对数均匀采样；动量项 $\beta$ 则通常取 $1-\beta$ 对数均匀(窗口大小 $\frac{1}{1-\beta}$ )。
- 实践方式：模型训练的同时调整超参数(算力不足) v.s. 多组超参数并行训练
批归一化(Batch Normalization)：对每个隐层的输入都执行归一化操作
- 直觉理解：对输入数据归一化有助于提升训练稳定性，加快收敛，基于相似原理，对网络内每个隐层的输入都执行归一化应该也有效果，这就是批归一化。不过相比输入归一化，BN增加了两个可调参数，对归一化结果进行缩放 $a = \beta + \gamma a_{\rm norm}$ ， $\beta,\gamma$ 可通过训练调整，让隐层特征能保持必要的分布信息(如 $\beta$ 取均值， $\gamma$ 取标准差，就恢复为归一化之前状态)。
  BN有助于缓解神经网络内部的协变量漂移，从而提升模型训练稳定性。协变量(covariate)是实验设计/统计学术语，字面意思是与因变量(dependent variable)协同变化的量，即所有与目标变量关联(协变)的量。统计学中通常将分析者关注并记录，用于分析与目标变量关系的变量，称为自变量(independent variable)或解释变量(explantory variable)，而协变量专指其余不受关注但同样影响目标变量的独立变量。这些协变量，有些会作为控制变量在实验时加以限制，有些可能完全不受控制，需要统计技术应对。不过在在机器学习领域，似乎没有这样的区分，所有模型输入都是协变量，而协变量漂移就是模型输入数据分布的变化，比如迁移学习中协变量漂移用于表示训练数据与实际应用之间的差异。当出现协变量漂移，即输入数据分布变化时，机器学习模型通常需要相应做适应调整。在神经网络内部，前一层输出作为后一层输入，模型训练时隐层输入在不断漂移，从而需要不断适应这种漂移，而BN限制了这种内部漂移(分布仅由 $\beta,\gamma$ 决定)，削弱了网络浅层对深层的影响，使网络深层的权重更稳健。
  此外，BN结合小批量梯度下降具有一定正则化效果。在小批量梯度下降时，BN在训练阶段是以每个batch的均值方差进行归一化，不同batch间的波动在网络内部引入一定噪声，有助于打破对固定节点的依赖。
- 具体位置：关于BN层放在激活函数之前还是之后学界存在争议，最初提出是放在激活函数前，Andrew Ng 也说放在激活函数前更常见(2017)，不过有研究提出放在激活函数后效果更好，尤其是对ReLU而言，具体可参考知乎上的讨论。
- 数据分批：小批量梯度下降时，训练阶段每个batch批归一化所用均值方差都不同，在测试阶段所用均值方差通常会采用指数加权平均获取。
- 后续改进：BN是对单个神经元(对应下图中通道 $\small C$ )的所有训练数据(沿数据 $\small N$ 方向)进行归一化。在batchsize很小时效果不好，且对于序列数据，每个批次内数据都长短不一，很难进行合理的归一化。因此对BN的后续改进都选择了放弃对批数据的依赖，转而针对单个输入，对隐层内的神经元的数据进行归一化，包括针对单个输入、整层神经元(特征图)的层归一化(LayerNorm)、针对单个输入、单个神经元的实例归一化(InstanceNorm)，以及介于两者之间对神经元分组处理的组归一化(GroupNorm)：
  
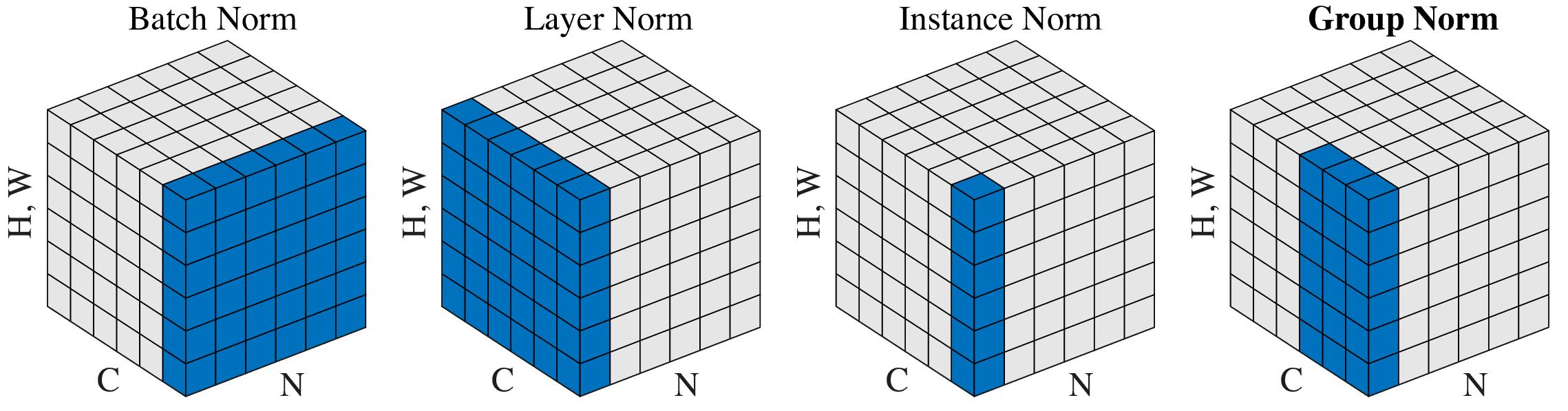
  层归一化适用于处理序列数据(RNN/LSTM)，实例归一化在处理图片风格转移等强调细节特征的任务时效果较好，而组归一化据称在batchsize很小时，效果较BN更优。

Strategy

实践策略：目标设定(指标选择/数据划分)、正交化调参、贝叶斯最优误差、误差分析

在改进提升模型时有很多中潜在选项(及其组合)，如收集更多数据、更多样的数据、训练更长时间、修改优化算法、更大/小的网络、随机失活、L2正则、调整网络构架等等，如何从中选择最佳策略组合，避免时间浪费十分关键。

正交化(Orthogonalization)调参：每次只专注单一目标
不同目标通常需要不同策略(组合)，正交化即每次只考虑单一目标，其他目标作为正交的选项。具体的将项目流程分为：训练、验证、测试、实战四个阶段；在训练阶段专注于降低模型损失的策略，如网络构架、更大网络、优化算法、增加训练时间等，无需过多考虑过拟合；在验证集检验时，则关注提升模型泛化性能，如正则化、更多训练数据、数据增强等，同时尽量不要破坏训练阶段成果；测试阶段则进一步检验模型整体表现，效果不理想意味着验证集“过拟合”了，应选择返回前一阶段，增加验证集数据量；最终如果在实战中模型表现不好，则可以考虑损失函数是否合理或者验证/测试集是否有代表性。Andrew Ng 这里再次强调其更倾向于将偏差与方差分开处理，而不是使用提前终止将两者耦合。

评价指标：单一数值指标有助于明确模型改进策略是否有效(注意不是损失)
当需要同时考虑多个评价指标时，一种策略是将多个指标综合为单一指标，如将精度(Precision)和召回率(Recall)综合为F-score。另一种策略则是从中选择一个核心指标作为改进目标(optiminzing metric)，其它指标仅作为“约束性”指标(satisficing metric)，模型只需要满足特定指标要求，而无需追求最优化。比如以正确率为关注目标，同时控制误报率不超过指定限制。
一开始无需强求尽善尽美，重要的是确定数据集/评价指标开始快速迭代优化，随着模型发开总会发现新的问题，比如可能模型评价指标很好，但存在一些不符合预期的表现，此时可能需要调整评价指标。
数据划分：保证开发/测试集同分布(Shuffle)，且能反映实际场景
数量比例上通常随数据量增加，开发、测试集占比可适当降低。中小数据集(~万)，经验选择为60/20/20或70/30；超大数据集(~百万)，开发、测试集可能取1%即可，即98/1/1。其次，在实际场景数据不足时，至少应保证开发/测试集与应用场景一致，从而使模型评估目标能反映实际情况，而训练集为了扩充数据量，数据分布可以与开发测试集不一致，而这种不一致可通过人工数据合成等手段改善。
当训练集与开发/测试集分布不一致，一个问题是训练集与开发/测试集效果反映的不再通常意义的上的方差，此时可在训练集中分出一组与训练集同分布的子集，作为开发集之前的过渡“开发”集，将模型方差与数据分布不一致两者的效果分开。如果模型在训练集上表现良好，但过渡开发集上表现很差，则需要重点改善方差；而如果过渡测试良好，但最终开发集效果很差，则问题在于数据分布的不一致。此时可手动分析数据特征，如语言识别应用场景中有更多噪声，就可以通过在训练数据中引入人工合成噪声，使训练数据接近应用场景。
贝叶斯最优误差：以人类表现作为其估计
对同样的训练/测试误差：当两者与人类表现差距较大时，进一步降低模型损失是首要目标；而当两者与人类表现差距不大，则降低模型方差，提升泛化可能才是重点。人类通常更擅长自然感知类任务，而在有海量数据的非自然感知任务中不少算法已超越人类表现，如线上推荐、物流规划、贷款审核、蛋白质折叠预测等等。
误差分析：搜集模型出错的数据，分析统计其中主要的数据类别，确定问题所在，用以指导后续投入方向。模型出错也可能数据标签本身错误。对于训练集，在数据量足够大，且标签错误随机时，通常问题不大，但如果存在系统性偏差则需要修正。对于开发测试集中的标签错误可作为单独一类，与其他错误分类数据一起统计对比，根据其重要性决定是否修正。而在修正时开发与测试集应一起修正，且需要注意可能存在标签出错，模型预测也出错，最终反而负负得正…
快速迭代：不要过度思考，划分数据并设定指标，快速建立初始系统quick&dirty，基于正交化策略选择迭代优化的方向
迁移学习：训练数据与应用场景数据/任务类型不同，预训练+微调
多任务学习：如多标签分类，多个二分类损失求和
端到端学习：无需手动设计特征，但需要大量训练数据。现实中很多任务可能过于复杂或难以收集足够数据，依然需要划分子任务，无法做到完全端到端。比如人脸识别，通常会拆分为面部检测和针对面部的识别。而自动驾驶任务则更是需要感知(车辆行人标识识别)、规划(路径规划)和控制(驾驶指令)等多个子系统的集成。

CNN

图片数据：CNN、ResNet、MobileNet、U-Net

CNN Intro

为什么要卷积：参数共享(卷积核)、稀疏连接(每层输出只与少部分输入有连接)
填充(padding)：valid、same 奇数卷积核才能实现same填充(同时有确定的中心像素)
步长(strides)：输入尺寸n×n，卷积核k×k，填充p，步长s，输出尺寸⌊(n+2p-k)/s⌋ + 1
互相关v.s.卷积：卷积核翻转，卷积网络中的“卷积”实际上通常是互相关(不翻转)
多通道：卷积核需要与输入有相同通道数，卷积核数又决定了输出通道数，每个卷积核/输出通道对应有一个偏置参数(标量)
池化(pooling)：同时对所有通道操作，通常不做填充，最常见的为k=s=2(不重叠)，由于池化层并没有可训练参数，通常不计入网络层数。

经典网络

基础网络：LeNet-5, AlexNet, VGG-16
ResNet：在深度方向拓展，提升训练的稳定性和效果，至少不比移除残差模块的浅层网络差。
1×1卷积(NIN, Network in Network)：对特征图逐位操作(pointwise)，实现通道间的混合(升维/降维)。
Inception：在宽度方向扩展，同时采用多种卷积核以及池化操作(拼接)，让模型自主确定各通路权重；先用1×1卷积压缩通道数(瓶颈层)，再做普通卷积，减少参数量。
MobileNet：深度可分离卷积，将普通卷积“拆解”为逐通道(depthwise)卷积与专门整合通道的1×1卷积，压缩参数量，同时减少计算量；V2中则先用1×1卷积升维(增加通道数)，之后逐通道卷积，再用1×1卷积恢复初始通道数，同时在整个模块外添加快捷连接。
EfficientNet：根据计算限制调整网络尺寸，输入维度(分辨率)、网络深度及网络宽度
实践：参考开源实现、使用预训练模型(迁移学习)、数据增强(翻转、旋转、变色)；模型集成

实践任务

物体检测

基础任务：识别定位(localization)、特征点检测(landmark)
滑窗检测(Sliding Windows) → OverFeat：通过卷积操作同步计算所有滑窗
候选区域(Region Proposal)策略：R-CNN, Fast R-CNN, Faster R-CNN
YOLO：You Only Look Once
- 边界框预测(Bounding Box) → 网格化(同时卷积)，数据标注时由物体中心位置确定所属网格
- 交并比IoU(Intersection over Union)：预测框与目标框面积交集/并集
- 非极大值抑制(Non-max Suppression)：对所有概率超过阈值的边界框预测，选择其中概率最大的作为预测框，移除所有与其“重叠”(IoU超过阈值)的边界框，即对单个物体只保留预测概率最大的边界框，之后对剩余候选框循环执行相同操作，直至处理全部候选框。
- 物体重叠：多个物体位于同一网格 → 锚框(Anchor Box)/先验框：每个位置同时考虑多种形状(尺寸、长宽比)的边界框，标签数据中包含预设的多个代表性的先验框，标注数据标签时物体归于与其形状最匹配的边界框(IoU最大)
  在网格足够细化时物体重叠其实并不多见，锚框的另一个作用是针对具体的数据，通过先验的边界框形状实现更好的进行处理。

语义分割

U-Net 语义分割(Semantic Segmentation) 逐像素分类
输出与输入维度一致：先卷积降维再升维，转置卷积(反卷积)

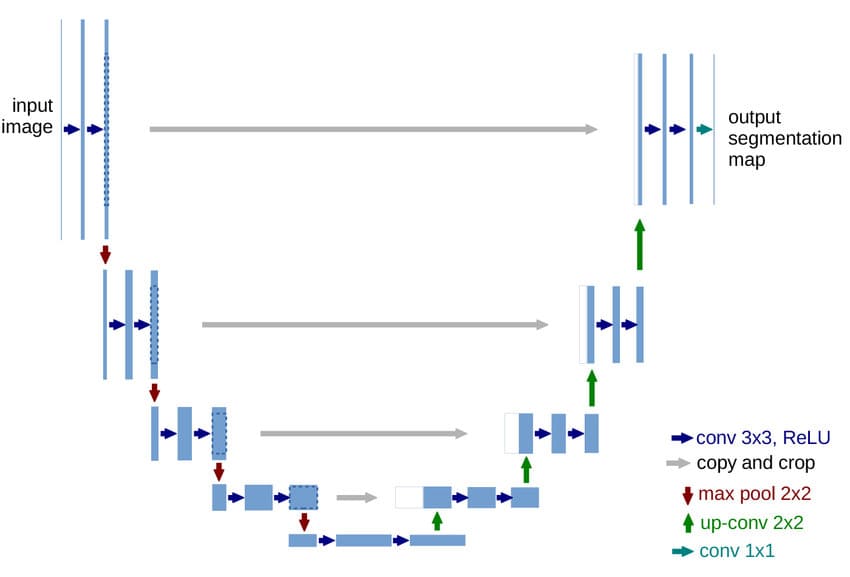
人脸识别

认证：判断是否为预设的目标对象 v.s. 识别：从数据库中找出匹配对象(或匹配失败)
每个人都是一个新分类，且通常只有个单样本(照片) → 放弃直接预测分类，转而学习图像的相似度函数(度量学习?)
孪生网络(Siamese Network)：用同一主干网络提取图片的特征，基于特征计算相似度 (DeepFace, FaceNet)
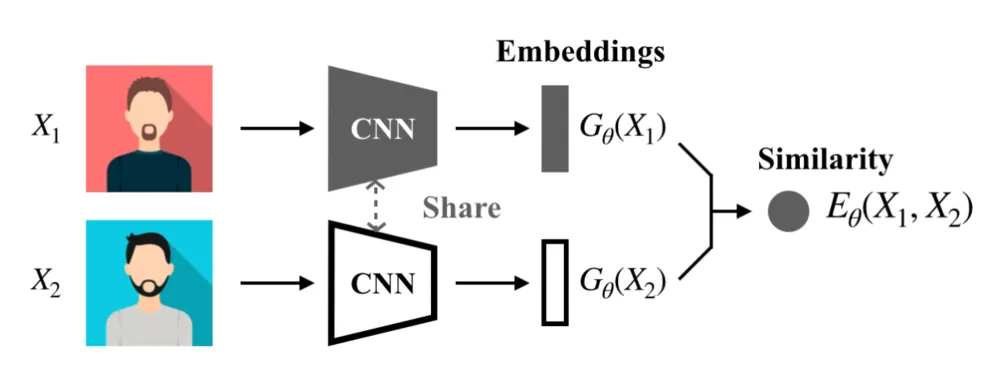应用模型时可预先计算数据库中的人脸特征，即加快了计算速度，也可避免数据泄露的风险
三元组损失(Triplet Loss)： $L(x, x^p, x^n) = \max\{ ||f(x), f(x^p)||^2 - ||f(x)-f(x^n)||^2 + \alpha, 0\}$ ，同时考虑基准与正例( $x, x^p$ )及基准与负例( $x, x^n$ )，训练目标为基准与正例的相似度远大于其与负例相似度(上面用2范数的平方计算)，用 $\alpha$ 调节两者之间的预期差距。

风格迁移

内容源C、风格源S、目标G → 内容损失 + 风格损失 $\alpha J_c(C,G) + \beta J_s(S,G)$
内容：类似孪生网络计算相似度，采用2范数平方 $J_c(C,G) = ||f(C) -f(G)||^2$
风格：每个通道对应某种特定特征模式，通道间相关则反映了各种特征模式的共现情况，某种程度上体现了图像风格。对各通道两两相关(特征图展开算内积)计算风格矩阵(Gram matrix)，并计算风格矩阵的相似度 $||S(C) -S(G)||^2$ 。最后，对网络各层都可计算风格矩阵相似度，整体风格相似度 $J_s(C,G) = \sum_{l} \lambda^{[l]} J^{[l]}_s(C,G)$ 。
权重选择：浅层体现局部特征，深层反映整体特征，因此加大浅层网络权重可获得更强的风格要求，而增加深层网络权重则会放松对风格的限制。
风格迁移中优化目标是内容图片C所对应的风格化目标图片G的像素点，而非网络的参数。网络本身采用预训练的网络用于图片特征提取，并在迁移过程中保持不变。

NLP

序列建模：RNN、LSTM、NTM、Attention、Transformer

RNN Intro

基础结构： $h_{t} = \tanh(W[h_{t-1};x_t] + b)$
梯度传递：时间反向传播BBTT
结构变种：N-to-1, 1-to-N, N-to-N, N-to-M(Seq2Seq)
情感分析、音乐生成、命名实体识别、语音识别、机器翻译
语言模型： $P(\text{Sequence}) = P(w_1, w_2, ..., w_T) = \prod_{t=1}^T p(w_t|w_{< t})$
序列生成：自回归生成+采样技术
字粒度模型：更小词表覆盖更多单词，减少未知词汇<UNK>；序列更长，更难训练
梯度消失(LSTM、GRU)、梯度爆炸(梯度裁剪Clipping)
RNN： $h_{t} = \tanh(W[h_{t-1};x_t] + b)$

Gate： $\begin{matrix} \tilde{h}_{t} =& \tanh(W_h[h_{t-1};x_t] + b_h) \\ u_{t} =& \sigma(W_u[h_{t-1}; x_t] +b_u) \\ h_{t} =& u_{t} \circ \tilde{h}_{t} + (1-u_{t}) \circ h_{t-1} \end{matrix}$

GRU： $\begin{matrix} u_{t} =& \sigma(W_u[h_{t-1}; x_t] +b_u) \\ r_{t} =& \sigma(W_r[h_{t-1}; x_t] +b_r) \\ \tilde{h}_{t} =& \tanh( W_h[r_{t} \circ h_{t-1};x_t] + b_h) \\ h_{t} =& u_{t} \circ \tilde{h}_{t} + (1-u_{t}) \circ h_{t-1} \end{matrix}$

LSTM： $\begin{matrix} i_{t} =& \sigma(W_i[h_{t-1}; x_t] +b_i) \\ f_{t} =& \sigma(W_f[h_{t-1}; x_t] +b_f) \\ o_{t} =& \sigma(W_o[h_{t-1}; x_t] +b_o) \\ \tilde{c}_{t} =& \tanh( W_c[h_{t-1};x_t] + b_c) \\ c_{t} =& i_{t} \circ \tilde{c}_{t} + f_{t} \circ c_{t-1}\\ h_{t} =& o_{t} \circ \tanh(c_{t}) \end{matrix}$
双向RNN：使用两个独立的RNN，分别由前向后和由后向前读取序列计算隐状态，之后将两者隐状态拼接在一起输入下一层
深度RNN：多层堆叠构成深度网络，将隐状态在层之间传递，需要注意的是LSTM结构的多层RNN中，只有 $h_{t}$ 是在层之间传递的，单元状态 $c_{t}$ 保持在层内。

Embedding

独热编码
分布式表示(词嵌入)：类比推理Analogy、嵌入矩阵
嵌入算法：NNLM、Word2Vec(CBOW, SKip-gram)、层次Softmax/负采样、GloVe

偏见消除：针对特定关注目标，对嵌入向量进行重新投影

识别偏见方向，以性别为例，可将he/she等性别相关词嵌入相减确定偏见方向
将性别无关的词嵌入向偏见维度(奇异值分解/主成分分析)之外的嵌入维度投影
词对均等(equalize pair)：将性别相关的相对词对，如father/mother均等分布

g1 = word_to_vec['woman'] - word_to_vec['man']
g2 = word_to_vec['girl'] - word_to_vec['boy']
g3 = word_to_vec['father'] - word_to_vec['mother']
gender_bias_axis = (g1+g2+g3)/3

def neutralize(word, word_to_vec, bias_axis):
    embd = word_to_vec[word]
    unit_bias_axis = bias_axis/np.linalg.norm(bias_axis)
    embd_bias = np.dot(embd, unit_bias_axis)*unit_bias_axis #bias_axis
    embd_debiased = embd - embd_bias
    return embd_debiased

def equalize(word_pair, word_to_vec_map, bias_axis):
    w1, w2 = word_pair
    w1_embd, w2_embd = word_to_vec[w1], word_to_vec[w2]
    unit_bias_axis = bias_axis/np.linalg.norm(bias_axis)

    w1_bias = np.dot(w1_embd, unit_bias_axis)*unit_bias_axis
    w2_bias = np.dot(w2_embd, unit_bias_axis)*unit_bias_axis

    mu = (embd_w1 + embd_w2)/2.0
    mu_bias = np.dot(mu, unit_bias_axis)*unit_bias_axis
    mu_orth = mu - mu_bias

    tmp = np.sqrt(np.abs(1-np.sum(mu_orth**2)))
    w1_bias_corrected = tmp * (w1_bias-mu_bias)/np.linalg.norm(w1_bias-mu)
    w2_bias_corrected = tmp * (w2_bias-mu_bias)/np.linalg.norm(w2_bias-mu)

    w1_embd_equalized = mu_orth + w1_bias_corrected
    w2_embd_equalized = mu_orth + w2_bias_corrected
    
    return w1_embd_equalized, w2_embd_equalized

Attention

Encoder-Decoder/Seq2Seq
NTM, 条件语言模型；贪婪搜索、集束搜索； BLEU评分
注意力机制：根据输入 $x_k$ $x_{k}$ 及输出 $s_{t-1}$ $s_{t - 1}$ 分配注意力，获取语境向量 $c_t$ $c_{t}$ ，用于输出解码
- 分配权重： $a_{tk} =\small \displaystyle \frac{\exp(e_{tk})}{\sum_j \exp(e_{tj})}, e_{tk} = \text{NN}(s_{t-1}, x_k)$
- 语境向量： $c_{t} = \sum_{k} a_{tk} x_k$
- 输出解码： $s_t = f(s_{t-1}, y_{t-1}, c_t)$
语音识别：CTC连接时序分类，将语音输入切分为很多小片段，每个片段对应一个输出，输出允许为空(特殊标记)，也可相同；将相邻的相同输出合并，并删除空输出作为最终输出。
触发词检测：触发词结束前标签取为0，刚结束时刻（或一小段时间）对应标签1。
Transformer网络：自注意力 $\text{softmax}(\frac{QK^T}{\sqrt{d_k}})V$ 、多头自注意力