当代物理发展到了什么水平 - 酱紫君|知乎

Posted on 2025-07-17 In Inspiring , PopSci Views: Waline:

现代物理是一种元理论，一种用来产生理论的理论。

历史回溯

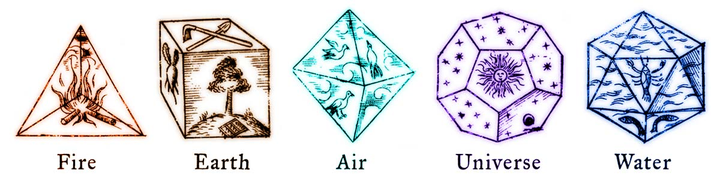
神圣几何体

在古希腊人眼中，一个正多面体的完美，源于它可以从不同角度旋转、翻转而保持自身形态不变。它们因其高度的旋转和反射对称性，被古希腊哲学家视为构成世界的基本原子形态。公元前6世纪，柏拉图在《蒂迈欧篇》中提出，宇宙是由一位神圣的工匠（Demiurge）依据完美的几何理念创造的，遵从神圣的对称性。他将物质世界的基本元素土气火水，与五种正多面体（Platonic Solids）一一对应：

正四面体（火）
正六面体（土）
正八面体（气）
正二十面体（水）

而最接近球形的正十二面体则象征着整个宇宙。

你想笑就笑吧，理论物理学家可笑不出来。因为他们的 $SU(5), SO(10), E_6, E_8\times E_8, E_{11}$ 和柏拉图提出的神圣几何没有本质区别。预言的一大堆元素粒子和柏拉图瞎掰的土气火水本质上是一样的。这种思潮被称为对称性优先（Symmetry First）。

诺特定理

时间快进到17世纪，科学的图景被艾萨克·牛顿彻底改写。牛顿用简洁而强大的数学语言构建了一个精确可预测的宇宙，他的万有引力定律能够精确预言行星的轨道、潮汐的涨落和苹果的坠落。这是一个前所未有的巨大成功。在牛顿之后的一百多年里，物理学家和数学家们沿着牛顿的道路解决复杂的力学问题，他们逐渐发现了一些极其有用的规律。他们注意到，在某些特定的物理过程中，尽管系统内部的细节在不断变化，但总有那么几个量保持恒定。时间来到在19世纪末，这些动量守恒、角动量守恒、能量守恒，三大守恒律已经成为经典物理学大厦的基石。它们是解决当时一切物理问题的强大工具，是每一个物理系学生的必修课。

然而，最早的理论物理学家在无聊的贤者时间思考这样一些问题：

为什么这些守恒律会存在？
它们之间有什么内在的联系吗？
它们只是恰好被上帝植入宇宙的三条独立规则吗？

18世纪末，约瑟夫·拉格朗日（Joseph-Louis Lagrange）和威廉·哈密顿（William Rowan Hamilton）对经典力学进行了重构。他们抛弃了牛顿力学中较为直观的力的概念，转而使用更为抽象的能量和作用量。在拉格朗日力学中，一个系统的所有动力学信息都被包含在一个称为拉格朗日量的函数 $L$ 中，它通常定义为系统的动能减去势能。物理系统真实的运动路径，将遵循最小作用量原理，让作用量 $\displaystyle S = \int L \,\mathrm{d}t$ 取极小值。一切力学都可以写成：

\delta S = 0

如果拉格朗日量中不显式地包含某个位置坐标 $q_i$ ，那么与该坐标对应的广义动量 $p_i = \frac{\partial L}{\partial \dot{q}_i}$ 就是一个守恒量。
如果拉格朗日量中不显式地包含时间 $t$ ，那么系统的总能量就是一个守恒量。

至此，对称性与守恒律之间的神秘联系，第一次在数学的语言中被清晰地勾勒了出来。从理论物理学家的哲思，变成了物理方程中实实在在的对应关系。物理学家们已经站在了新世界的大门前，他们手中握着对称性和守恒律这两把钥匙，但却没有意识到它们本就是一体两面。

所有的伟大进步都要从一场打破安逸的危机开始。20世纪初的物理学界，三大支柱，牛顿力学、麦克斯韦电磁学、统计热力学，取得了辉煌的成功。经典物理学的大厦已经完工，就等着封顶，只是暂时天气不大好，有两朵乌云。在宏观层面，爱因斯坦在1905年和1915年相继提出了狭义与广义相对论，彻底颠覆了牛顿的绝对时空观，将空间与时间成了一个可以被物质和能量弯曲的整体。在微观层面，普朗克的量子假说和玻尔的原子模型则揭示了一个离散、概率性和反常量子世界，也同样颠覆了物理学家们的世界观。

1915年，德国哥廷根大学。数学家大卫·希尔伯特（David Hilbert）和菲利克斯·克莱因（Felix Klein）正致力于理解爱因斯坦刚刚出炉的广义相对论。他们对其一个核心问题感到困惑：

在这样一个时空可以任意弯曲的理论中，我们习以为常的能量守恒定律还成立吗？
如果成立，它应该以何种形式表达？

这个问题棘手至极。在牛顿的世界里，能量守恒是明确的。但在广义相对论中，由于时空本身是动态的，定义一个在所有坐标系下都守恒的能量变得异常困难。为了解决这个难题，希尔伯特邀请了当时在抽象代数和不变量理论领域颇有建树的诺特来到哥廷根。

诺特没有直接陷入广义相对论复杂的张量计算中，她而是采取了一种更统一、更抽象的视角来思考问题的本源：

守恒律究竟从何而来？

诺特思考发现，不应该局限于某个具体的物理系统，而是要找到任何一个可以用作用量原理描述的物理系统的普遍性质。经过近三年的潜心研究，在1918年，诺特发表了《不变量变分问题》（Invariante Variationsprobleme）。在这篇论文中，她证明了一个影响深远的定理，后世称之为诺特定理（Noether’s Theorem）。该定理指出：

对于一个物理系统，如果其拉格朗日作用量在某个连续的全局变换下保持不变，那么必然存在一个与之对应的守恒量。

这个断言是革命性的。它将物理学家们长期以来视为孤立的、经验性的守恒定律，提升到了由对称性这样的第一性原理推导出的必然结论：

空间平移对称性即为动量守恒
空间旋转对称性即为角动量守恒
时间平移对称性即为能量守恒

诺特定理的发表，彻底改变了理论物理学家的世界观。在此之前，物理学家通过实验发现动量守恒、能量守恒这些规律，并将它们奉为神圣的法则。这些守恒律就像是上帝在创世之初设下的几条基本公理，我们只能接受并使用它们。在此之后，物理学家的角色转变为宇宙法则的架构师。理论物理成为一种元理论。对称性不再是描述物体外观的美学词汇，而是跃升为更根本、更具创造性的第一性原理。

这种视角的革命性转变带来了全新的研究范式。与其费力地去猜测复杂现象背后的动力学方程，不如先去寻找这个系统可能拥有的对称性。一旦你确定了一个对称性，诺特定理就会自动为你指明一条通往相应守恒律的康庄大道。

古典对称性

19世纪末到20世纪中叶，物理学家们手握诺特定理，拿着锤子看啥都是钉子。在这个阶段，科学家们将对称性思维应用到了从宏观晶体到微观粒子、从经典力学到广义相对论的广阔领域。这个时期的对称性，我们可称之为“古典对称性”，它们大多是定义在全局时空几何的对称性，要求整个物理系统或时空背景遵循同一个变换规则。

在固体物理学中，数学家谢恩菲斯（Schoenflies）和物理学家费奥多罗夫（Fedorov）独立地运用群论，完成了对三维空间中所有可能的晶体对称性结构的系统性分类，得出了不多不少正好230种空间群。在分子物理学中，一个分子的对称性可以用点群描述，这直接决定了它的振动模式、化学反应活性以及光谱特征。对称性分析进一步扩散到化学界，成为了化学家简化复杂计算、预测分子性质的强大工具。

诺特定理下的相对论则将对称性的概念提升到了一个全新的抽象维度，那就是时空本身的对称性。爱因斯坦在1905年提出的狭义相对论，核心出发点之一本身就是一种深刻的对称性：

物理定律在所有惯性参考系中都具有相同的形式。

这意味着无论你是在静止的实验室里，还是在匀速飞行的飞船上，麦克斯韦的电磁学方程、力学定律都应该完全一样。

为了让麦克斯韦方程组在这种变换下保持形式不变，传统的伽利略变换必须被一种新的遵从守恒性的时空变换所取代。这就是洛伦兹变换，洛伦兹变换将空间和时间交织在一起，形成了四维的闵可夫斯基时空。

结合诺特定理揭示的空间平移、时间平移和旋转对称性，再加上洛伦兹变换，这些操作共同构成了一个更大的对称群，这个群被称为庞加莱群（Poincaré Group）。狭义相对论时空所拥有的最基本的全局对称性也被称为庞加莱对称性，它包含了10种基本的连续变换：

3 个空间平移对称性，对应动量守恒
1 个时间平移对称性，对应能量守恒
3 个空间旋转对称性，对应角动量守恒
3 个洛伦兹对称性，对应质心运动守恒

所有符合狭义相对论的物理理论，其数学形式都必须是庞加莱群的协变形式。

爱因斯坦并未满足于狭义相对论，他追问：

为什么物理定律只在惯性参考系这个特权阶层中保持不变？
能否让它在所有参考系中都具有相同的形式？

这个对更普适对称性的追求，最终导向了广义相对论。其核心原理是广义协变性原理：

物理方程的形式不应依赖于观察者所使用的具体坐标系。

这是一个极其强大的对称性要求，而为了满足这一要求，爱因斯坦发现必须引入时空的弯曲，并将引力解释为时空几何本身。

另一方面，保罗·狄拉克在1928年提出的狄拉克方程，这个方程完美地描述了电子等自旋为1/2的费米子，并且它天然地满足庞加莱对称性。匈牙利物理学家尤金·维格纳（Eugene Wigner）通过对庞加莱群的表示论进行深入分析，从纯数学的角度证明了：

量子力学中的基本粒子可以被严格地定义为庞加莱群的一个不可约表示。

这意味着，粒子的质量和自旋不是任意的参数，而是时空基本对称性所允许的、离散的、内在的属性。

至此，对称性原理已经取得了辉煌的成就。它统一了时空几何，为守恒律找到了根源，分类了基本粒子，预言了反物质。然而，这些古典对称性还有一个致命问题，它们都是全局的。

现代物理

规范对称性

全局对称性进行一个对称变换时，必须对整个宇宙的所有时空点同时、以完全相同的方式进行操作。在进行空间平移时，你必须将宇宙中的每一个粒子都朝着同一个方向移动完全相同的距离。在旋转时，也必须让整个宇宙绕着同一个轴旋转同样的角度。这种全局性的要求，违背了广义相对论。爱因斯坦已经告诉我们，时空是动态的、局域的，一个地方发生的事情需要时间才能传播到另一个地方。那么，一个对称性变换怎么可能瞬间影响到整个宇宙呢？宇宙必然不遵从全局对称性。

于是物理学家们开始思考一个更为激进、也更为深刻的问题：

如果一个对称性不仅在全局上成立，而且可以在时空的每一个点都独立地、任意地进行，物理世界会是什么样子？

设想一下，在量子力学中，描述一个电子的波函数 $\psi(x)$ 有一个相位。我们可以将整个宇宙中所有电子的波函数都乘以一个相同的相位因子 $e^{i\alpha}$ ，而物理结果不变。这是全局的 $U(1)$ 对称性。但现在，我们提出一个更苛刻的要求，我们希望在每一个时空点 $x$ 都能独立地选择一个不同的相位 $\alpha(x)$ ，进行变换 $\psi(x) \to e^{i\alpha(x)}\psi(x)$ ，而物理定律依然保持不变。

这个局域对称性看起来无论如何都无法满足。因为描述粒子运动的方程中包含导数项 $\partial_\mu \psi$ ，在局域相位变换下，这个导数项会产生一个额外的、不想要的项 $i(\partial_\mu \alpha(x)) \psi(x)$ ，从而破坏方程的形式。那么，我们可不可以想办法修正这个局域对称性？我们不如引入一个补偿场 $A_\mu(x)$ ，它的作用就是精确地抵消掉那个不想要的项。而为了让理论在局域变换下保持不变，这个新引入的规范场 $A_\mu$ 自身也必须遵循特定的变换规则。

物理学家们突然发现，这个被强行引入以满足局域对称性要求的规范场，它的量子化激发态，竟然就是传递相互作用的粒子！就这样，对对称性原则的终极追求意外地为我们揭示了宇宙基本力的起源。这一思想后来系统化成了规范对称性（Gauge Symmetry），它是构建粒子物理学标准模型的核心。对称性不再仅仅是描述现有物理定律的属性，它变成了创造物理定律本身的引擎。一场更加深刻的物理学革命即将拉开序幕。

量子电动力学

第一个被规范原理完美解释的是电磁力。在量子力学中，一个带电粒子由一个复数波函数 $\psi(x)$ 描述。波函数的物理意义在于其振幅的平方 $|\psi(x)|^2$ ，这代表了在时空点 $x$ 发现该粒子的概率。这意味着我们可以将波函数乘以一个任意的、固定的相位因子 $e^{i\alpha}$ ，而物理观测结果完全不变：

\psi(x) \to e^{i\alpha} \psi(x) \quad \implies \quad |\psi(x)|^2 \to |e^{i\alpha}\psi(x)|^2 = |\psi(x)|^2

这种变换构成了一个数学群，称为 $U(1)$ 群，它本质上是复平面上的旋转。由于这里的 $\alpha$ 是一个常数，对所有时空点都一样，所以这是一种全局对称性。根据诺特定理，它对应着电荷守恒。

如果这个相位变换可以在时空的每一个点 $x$ 独立进行呢？也就是说， $\alpha$ 不再是常数，而是时空的函数 $\alpha(x)$ ：

\psi(x) \to e^{i\alpha(x)} \psi(x)

这个要求被称为局域 $U(1)$ 规范对称性。当我们尝试将这个变换应用到描述电子运动的物理方程中时，对波函数的时空导数项 $\partial_\mu \psi$ 衡量了波函数在邻近点之间的变化率。在局域变换下，导数项会变成：

\partial_\mu \psi(x) \to \partial_\mu (e^{i\alpha(x)} \psi(x)) = e^{i\alpha(x)} (\partial_\mu \psi(x) + i(\partial_\mu \alpha(x)) \psi(x))

除了我们期望的相位因子 $e^{i\alpha(x)}$ 外，还多出了一个垃圾 $i(\partial_\mu \alpha(x)) \psi(x)$ 。

这个多余的项破坏了方程原有的形式，打破了对称性！为了修补这个局域对称性，规范场论要求，当 $\psi(x)$ 进行相位变换时，这个新场也必须同时进行一个特定的变换：

A_\mu(x) \to A_\mu(x) - \frac{1}{e}\partial_\mu \alpha(x)

然后，我们用协变导数 $D_\mu$ 来替换掉原来的普通导数 $\partial_\mu$ ：

D_\mu = \partial_\mu + ieA_\mu

经过一番计算，我们惊喜地发现，规范场 $A_\mu$ 的变换不多不少，正好完美地抵消了那堆垃圾项，最终结果是：

D_\mu \psi(x) \to e^{i\alpha(x)} (D_\mu \psi(x))

物理方程的形式在局域变换下同样保持不变，不过还有一个问题，这个规范场 $A_\mu$ 的物理意义是什么？

它就是电磁场的四维矢量势，而它的量子化激发就是传递电磁力的光子（Photon）！这个推导表明，电磁力的存在，可以被看作是宇宙为了维护电子波函数局域相位不变性而必须付出的代价。麦克斯韦方程组，可以被理解为 $U(1)$ 规范对称性的必然结果。

不仅如此，这一理论的量子化版本，量子电动力学也取得了空前的成功。它预言的电子反常磁矩和兰姆位移等物理量，其理论计算值与实验测量值的符合程度达到了小数点后十几位，是有史以来最精确的物理理论预言。

电弱统一理论

电磁力的成功规范化极大地鼓舞了物理学家，他们将目光投向了弱相互作用，即导致原子核发生放射性衰变的力。弱力与电磁力有很大的不同，它非常弱，而且作用范围极短。这意味着传递弱力的粒子必须非常重，不能像光子那样是无质量的。

物理学家发现，某些粒子在弱相互作用中表现得像一个二重态，这启发人们使用一个比 $U(1)$ 更复杂的对称群。而 $SU(2)$ 的局域规范化，会自然地产生三种规范玻色子来传递弱力。可是一个纯粹的规范理论要求其规范玻色子必须是无质量的。这与弱力作用范围极短的实验事实严重矛盾。

20世纪60年代，格拉肖、萨拉姆和温伯格大胆地假设：

在极高的能量下，电磁力和弱力是同一种力的不同表现，它们统一在一个更大的对称群 $SU(2) \times U(1)$ 之下。
在这个统一的框架下，存在四种无质量的规范玻色子。
而我们所处的低能世界中，这个完美的 $SU(2) \times U(1)$ 对称性被自发地破缺了。

一根竖直放置的铅笔，它的状态是旋转对称的。但这个状态不稳定，任何微小的扰动都会使它倒向某一个随机的方向。一旦倒下，铅笔躺在桌上，系统就不再具有原来的旋转对称性了，尽管控制铅笔运动的物理定律本身仍然是旋转对称的。在电弱理论中，扮演这个扰动角色的是遍布全宇宙的希格斯场（Higgs Field）。

在宇宙早期温度极高时，希格斯场处于对称的激发态。随着宇宙冷却，它凝结到一个非零的真空期望值上，就好比水蒸气凝结成水一样。这个过程破坏了原有的 $SU(2) \times U(1)$ 对称性，但保留了一个 $U(1)$ 子群的对称性。最终这个对称性破缺的过程产生了合理的结果：

四种初始的无质量规范玻色子通过与希格斯场相互作用，重新组合。
其中三种获得了质量，变成了传递弱力的 W⁺, W⁻ 和 Z⁰ 玻色子。
它们的质量约是质子质量的80-90倍，完美解释了弱力的短程性。
剩下的一种玻色子没有获得质量，保持为光子，它所对应的对称性就是我们熟悉的电磁学 $U(1)$ 对称性。

该理论还预言，希格斯场本身也应该有一个量子化的激发，即一种全新的基本粒子，希格斯玻色子。2012年，经过数十年的寻找，LHC 发现了一个质量约为125 GeV的新粒子，其性质与标准模型预言的希格斯玻色子高度一致。

电弱统一理论被彻底证实，由此开启了理论物理学家人人神棍，天天预言的现状。

量子色动力学

最后一块拼图是强相互作用理论。强力将夸克束缚在一起形成质子和中子，再将质子和中子束缚成原子核。物理学家为了解释夸克的一些奇特组合，引入了一种新的量子荷，这种特殊属性被称为色荷（Color Charge）。色荷有三种类型，为了方便记忆，人们称之为红、绿、蓝，其本身与视觉颜色毫无关系。相应的反夸克则带有反红、反绿、反蓝。

所有在自然界中能被自由观测到的粒子，都必须是色中性的，或者说无色的。这种在三种色荷之间进行变换的对称性，可以用 $SU(3)$ 群来描述。将规范原理应用于这个局域的 $SU(3)$ 对称性，便诞生了描述强力的量子色动力学。传递强力的规范玻色子被称为胶子（Gluon）。

$SU(3)$ 对称性要求存在八种不同的胶子。与不带电荷的光子不同，胶子自身也携带色荷。胶子的自相互作用导致了两种奇特的现象：

渐近自由（Asymptotic Freedom）：在极高的能量下，或极短的距离内，夸克之间的强相互作用会变得非常弱，夸克表现得如同自由粒子一般。
色禁闭（Color Confinement）：在较低的能量下，或较长的距离上，夸克之间的力会随着距离的增加而快速增强。这股力是如此之大，以至于将一个夸克从质子中单独拉出来所需要的能量，足以在真空中创造出一对新的夸克-反夸克，而新产生的夸克会立即与被拉的夸克结合，形成新的无色粒子。

因此，单个的夸克和胶子永远无法被独立观测到，它们被永久地囚禁在强子内部。至今为止，所有试图寻找自由夸克的实验都以失败告终，这为色禁闭提供了强有力的旁证。

至此，基于局域规范对称性原理的粒子物理学标准模型大厦宣告落成。它以抽象的数学结构 $SU(3) \times SU(2) \times U(1)$ 为根基，通过规范化和对称性破缺，精准地描绘了除引力之外的三种基本力以及所有已知基本粒子的行为。对称性，已经从一种哲学原则，跃升为物理定律的设计法则。

Lie 代数

规范对称性仅仅通过要求物理定律在时空每一点都满足某种内部的、局域的对称性，我们便凭空推导出了所有的微观现象。那么问题来了：

$U(1)$ , $SU(2)$ , $SU(3)$ 它们为何如此特殊，能被宇宙选中，成为构建微观物理学的基石？

挪威数学家索菲斯·李（Sophus Lie）在19世纪末发明了天真谎言理论，在当时被视为纯粹的数学抽象，却在百年后成为了理论物理学的核心支柱。

想象一下你能对一个物体进行的所有连续变换。旋转一个球体，你可以将它绕Z轴旋转 $10^\circ$ ，也可以旋转 $10.001^\circ$ ，或是任意一个微小的角度。所有可能的旋转角度构成了一个连续的集合。这些变换操作本身，以及它们的组合规则，就构成了一个李群。

简单来说，一个李群既是一个群，满足封闭性、结合律、有单位元和逆元。又是一个光滑的流形，这意味着你可以在这个群上平滑地从一个变换移动到另一个变换。 $SO(2)$ 或 $U(1)$ 是最简单的李群，描述了二维平面上的旋转。它的图像就是一个圆，参数是旋转角度 $\theta \in [0, 2\pi)$ 。

但是一般情况下，直接处理整个李群通常很复杂。数学家和物理学家发现了一个巧妙的捷径，不如研究这些变换的无穷小版本。

李代数是李群在单位元附近的线性近似。李代数由一组称为生成元的基底构成。每个生成元代表一个基本、无穷小的变换方向。三维空间中的旋转可以由绕 $x, y, z$ 轴的三个无穷小旋转生成元 $J_x, J_y, J_z$ 构成。

李代数最核心的结构是李括号，通常记为： $[A, B] = AB - BA$ 它描述了两个无穷小变换的先后顺序如何影响最终结果：

如果 $[A, B]=0$ ，说明 A 和 B 两种变换互不干涉，可以随意交换顺序，这样的群称为阿贝尔群，如 $U(1)$ 。
如果 $[A, B] \neq 0$ ，说明顺序至关重要，这样的群称为非阿贝尔群，如 $SU(2)$ 和 $SU(3)$ 。

李代数捕捉了李群最本质的局部结构。一旦我们知道了生成元以及它们之间的李括号关系，这就确定了结构常数，原则上可以重构出整个李群。现在回到关键问题：

宇宙为何选择了 $U(1), SU(2), SU(3)$ 这些群？
难道不是任何群都可以吗？

物理学家深入研究后发现，物理世界对它的对称性语言有着极其苛刻的要求。许多在数学上完美的群，一旦用于描述物理现实，就会导致荒谬的反物理现象。

首先不能使用像对称群 $S_5$ 这样的离散群来描述基本力的规范对称性。 $S_5$ 的操作是离散的跳跃，比如将物体1和物体3交换，你无法做到交换一半。如果一个规范对称性由离散群描述，那么它对应的力也将是断续的。诺特定理的核心是连续对称性对应守恒律，离散对称性无法保证能量、动量这些连续守恒量的存在。物理定律将变得支离破碎，时空本身也失去了平滑性。

还有一个更微妙但更深刻的筛选标准，直观上可以理解为对称必须是有界的并且封闭的。李群可以分为紧致 (Compact) 和非紧致 (Non-compact) 两类。

一个圆周或球面，你无法在上面永远朝一个方向走下去而不触及边界或重复路径，他们是紧致的。
一条无限长的直线或一个平面，你可以永远走下去，永远不重复，这就是非紧致的。

描述内部规范对称性的李群必须是紧致的，假设我们选择了一个非紧致的李群，比如用 $GL(2, \mathbb{R})$ 来构建一个物理理论，这会导致各种反物理的现象。比如概率不守恒，违反量子力学，如果我们使用非紧致群，其变换通常会改变量子态的长度，导致总概率要么大于1要么小于1。这意味着粒子可以凭空产生或消失，这彻底摧毁了量子理论的根基。另一方面粒子多重态会无限多，非紧致李群的幺正表示几乎都是无限维的。如果弱相互作用由某个非紧致群描述，那么电子将会有无穷多种伴随粒子，形成一个无限大的粒子家族。这与我们在加速器中观测到的有限粒子谱完全矛盾。

总之物理学通过幺正性原则，从无穷多的李群中筛选出了紧致李群作为描述内部对称性的唯一合格候选者。这就是为什么标准模型的规范群 $U(1) \times SU(2) \times SU(3)$ 全都是紧致李群。

不过有个特例，那就是洛伦兹群，它描述了时空对称性，可它是非紧致的。这没问题吗？老铁没毛病，因为洛伦兹群描述的是外部时空对称性，而非粒子的内部对称性。它的非紧致性恰恰解释了物理现象，Boost 参数是相对速度，它可以无限趋近光速，这是一个无界的参数。此时对应的无限维表示也对应着一个粒子可以拥有连续变化的、无限多种动量状态这一物理现实。

在数学家们的通力合作下，埃利·嘉当 (Élie Cartan)完成了对所有单李代数的完全分类。就像化学元素周期表一样，它们构成了一个清晰的图谱：

$A_n$ ：对应于特殊酉群 $SU(n+1)$ 。
$B_n$ ：对应于奇数维空间的正交旋转群 $SO(2n+1)$ 。
$C_n$ ：对应于辛群 $Sp(2n)$ 。
$D_n$ ：对应于偶数维空间的正交旋转群 $SO(2n)$ 。
例外李群： $G_2, F_4, E_6, E_7, E_8$

这个完整的分类为物理学家们指明了所有可能的对称性。最奇怪的就是五个例外李群，这些群在被发现之初被认为是纯粹的数学怪胎，没有任何用处。然而，物理学家们很快意识到，正是这些看似例外的结构，可以为我们解答那些标准模型和经典李群无法触及的、最深层次的物理谜题。

交错代数

$G_2$ 是八元数代数的自同构群，也就是所有保持八元数乘法规则不变的变换所构成的群。它是最小的例外李群。

M理论预言我们的宇宙有11个维度，其中7个维度需要被紧致化。如果这7个维度被卷曲成一个具有 $G_2$ 对称性的特殊 $G_2$ 流形，那么得到的四维有效理论就会呈现出某些与现实世界惊人相似的特性，能够自然地产生我们需要的粒子谱和超对称性。

Albert 代数

在量子力学中，物理可观测量由算符表示，这些算符的乘积不满足交换律，但它们的对称化乘积 $A \circ B = \frac{1}{2}(AB + BA)$ 却具有良好定义的物理意义。这种新的乘法结构被称为乔丹代数。数学家们发现，大多数乔丹代数都与经典的矩阵代数有关，但存在一个例外：一个由 $3 \times 3$ 的八元数矩阵构成的27维代数，它无法用任何传统的矩阵代数来表示。这个结构被称为阿尔伯特代数（Albert Algebra）。

而 $F_4$ 是这个例外阿尔伯特代数的自同构群。物理学家猜想，它可能与量子引力的内在逻辑，或者某种更深层次的时空代数有关。

手性理论
标准模型的一代费米子，包含左手和右手粒子，共15个，加上一个右手中微子，总共16个粒子，可以完美地嵌入到 $SO(10)$ 群的一个16维旋量表示中。

$E_6$ 最小复表示是 27维的，这个27维表示可以被分解为：

\mathbf{27} \rightarrow \mathbf{16} + \mathbf{10} + \mathbf{1}

这意味着一个 $E_6$ 的基本粒子多重态，不仅优雅地包含了 $SO(10)$ 的整个粒子世代，还额外预言了一组新的奇异夸克和轻子（ $\mathbf{10}$ ）以及一个惰性中微子（ $\mathbf{1}$ ）。这为解释暗物质、中微子质量等超越标准模型的新物理提供了丰富的可能性。

$E_6$ 能够自然地处理弱相互作用所要求的手性，区分左手和右手粒子。而且许多超弦理论的紧致化结果，其低能有效理论的规范群恰好就是 $E_6$ 。

黑洞熵

根据贝肯斯坦-霍金公式，黑洞的熵正比于其视界面的面积：

S_{BH} = \frac{A}{4G\hbar}

在某些特定的超引力或弦论模型中，可以构造出一种特殊的极值黑洞。对这类黑洞，物理学家可以精确地计算其微观状态的数量。对于在四维时空中的某类超引力理论，其黑洞熵的计算公式，由一个 $E_7$ 群的不变量来精确控制！

理论中所有场的荷构成了一个56维的表示空间，这个空间的对称性，被称为U-对偶群。这个群恰好就是 $E_7$ 的一个实形式 $E_{7(7)}$ 。而黑洞的熵，可以通过计算这些荷在这个 $E_7$ 对称性下的一个四次不变量得到。

杂化弦理论

描述弦振动的模式被分为左行波和右行波。为了消除理论中的反常，实现量子自洽性，理论要求右行波具有10维时空的超对称性，而左行波生活在26维时空，其中16个额外的维度必须被紧致化到一个16维的环面上。数学家证明，这个16维内部空间的对称性规范群，必须是 $E_8 \times E_8$ 或 $SO(32)$ 之一，没有第三种选择。

$E_8$ 是弦论为了维持其自洽性而自己长出来。 $E_8 \times E_8$ 的杂化弦理论在低能极限下，可以自然地产生一个包含引力，并且规范群为 $E_6$ 的大统一模型。它一度被认为是万有理论的头号候选。

大统一理论

标准模型取得了空前的成功，它精确地描述了电磁力、弱相互作用和强相互作用，以及所有已知的基本粒子。物理学家们不禁发出一个大胆的猜想，这三股看似独立的力量，会不会只是一个更宏大、更本源的统一力量在我们的低能量世界中呈现出的不同侧面？就像电和磁在麦克斯韦的理论中被统一为电磁力一样，强、弱、电这三种力会不会在宇宙极早期的高温高能环境下，也统一为一种大统一力？

寻找一个更大的、单一的规范群，将标准模型作为其子群完全包含在内：

$G \supset SU(3)_C \times SU(2)_L \times U(1)_Y$

这就是大统一理论（GUT）的核心思想。

GUT 不仅仅是一个哲学猜想，它也有许多可被验证的预测，是诺贝尔奖的常客。物理学家发现，基本力的强度并不是一成不变的，而是随着能量的变化而变化的。

电磁力 $U(1)$ ：由于真空极化效应，其强度随能量升高而增强。
强相互作用 $SU(3)$ ：由于胶子的渐近自由，其强度随能量升高而减弱。
弱相互作用 $SU(2)$ ：行为与强力类似，强度随能量升高而减弱。

将这三条曲线向高能量区域外推后发现，它们虽然没有精确地交于一点，但却朝着一个非常小的区域汇聚。这暗示，在某个极高的能量尺度 GUT能标下，它们很可能就是同一个值，这个值被称为统一的耦合常数 $\alpha_G$ 。而且如果我们在标准模型中引入超对称（Supersymmetry），这个几乎交汇就变成了完美的交点。

然而 GUT 也做出了一个至今仍未被证实的预言：

质子会衰变。

既然夸克和轻子被置于同一个大家族中，就必然存在一种新的相互作用，能够将夸克转变为轻子。这种变换由 GUT 预言的新的超重规范玻色子来传递。这意味着质子并非永恒不朽，而是有极其微小的概率衰变成更轻的粒子：

p \to e^+ + \pi^0

世界各地的科学家建造了巨大的地下探测器，如日本的超级神冈探测器（Super-Kamiokande），其本质就是一个装满超纯水、被上万个光电倍增管包围的巨大水箱，时刻等待着捕捉质子衰变发出的微弱闪光。然而，年复一年，质子衰变的信号始终没有出现。

当代物理

Kac-Moody 代数

GUT 身上大大的问号不止于此，当物理学的探索深入到引力、弦论以及宇宙奇点这些更为奇异的领域时，一个严峻的问题浮现了：

有限维的对称性，还够用吗？

无论是 $SU(5)$ 、 $SO(10)$ 还是宏伟的 $E_8$ ，它们虽然能够统一规范相互作用，但在处理引力时，都显得力不从心。引力场在每个时空点都有其自由度，这构成了一个无限维的相空间。试图用一个拥有有限数量生成元的群，去完整描述一个拥有无限自由度的理论，有点搞笑。

物理学迫切需要一种能够容纳无限可能性的数学语言。物理学家们需要的，不再仅仅是一个能为粒子的静态对称性，而是一个能够描述系统如何演化的动态对称性原理。幸运的是，在物理学家不知道怎么爬山时，数学家早就爬到不知哪里去了。

早在 20世纪60年代末，数学家维克多·卡茨（Victor Kac）与罗伯特·穆迪（Robert Moody）就独立地找到了推广有限维李代数的系统性方法，创立了卡茨-穆迪代数（Kac-Moody Algebras）。

有限维李群告诉我们，在一个特定的舞台上，粒子有哪些对称的形状。无限维卡茨-穆迪代数则告诉我们，这个舞台本身是如何搭建的，粒子如何出现、消失。

有限型（Finite Type）

卡茨-穆迪理论的第一项成果，就是再次证明了有限维李代数的分类是完备的。它告诉我们，我们之前找到的那些对称性确实就是全部了，没有遗漏。

仿射型（Affine Type）

用有限李群作为单块瓷砖，铺满一整面墙，会展现出一种周期性。这种无限、周期性的平铺图案，就对应着仿射卡茨-穆迪代数。它的生成元数量变成了无限多，但这种无限是以一种高度有序、可预测的方式增加的。除了瓷砖本身的对称性，它还多了一种平移对称性，这种有序的无限恰好是描述特殊物理系统所需要的语言。

在弦论中，基本客体是一根振动的弦，它在时空中扫过的轨迹形成一个二维的世界面，描述这个二维世界面内在对称性的，正是仿射卡茨-穆迪代数。弦的每一种振动模式，都对应着代数中的一个状态。

二维共形场论（2D CFT）是研究相变临界点和弦论的强大工具，其底层的对称性构造几乎完全由仿射卡茨-穆迪代数支配。仿射代数是迈向无限维对称性的前哨站，它向我们展示了无限不一定意味着混乱，也可以是充满秩序的。

双曲型（Hyperbolic Type）

严格意义上来说这才是真正的无限李群。就像埃舍尔（M.C. Escher）的画作《圆之极限》那样，瓷砖越靠近边界就变得越小，图案以一种指数级的速度疯狂增殖，永不重复。

这就是双曲型卡茨-穆迪代数。它们的生成元数量也是无限的，但其增长方式是爆炸性的、混沌的。其内部结构极其复杂，根的数量和关系呈指数级增长。在发明后的很长一段时间里，它们被数学家视为缺乏应用的数学怪物。

在杂物堆里沉寂多年以后，当物理学家试图描述那些我们现有理论完全失效的场景时，双曲代数的这种受控混沌特性出人意料的发挥了其优势。在宇宙创生的最初瞬间，时空的概念已经瓦解，物理状态在极短时间内经历剧烈、混沌的振荡。

在寻求统一所有基本力的M理论中，物理学家需要一个能容纳引力和时空本身的庞大对称性结构。一些巨大复杂的双曲代数被提议作为M理论潜在的终极对称性。双曲型代数告诉我们，在看似最混乱、最复杂的系统中，也可能隐藏着深刻的、尽管无限复杂的代数对称性。

宇宙在趋近大爆炸奇点时的动力学，由 $E_{10}$ 对称性支配。

这个猜想由法国物理学家 Thibault Damour 等人提出，旨在解决将时间回溯到 $t \to 0$ 的那一刻，物理学将何去何从？

$E_{10}$ 是一个双曲型卡茨-穆迪代数。我们熟悉的例外李代数 $E_8$ 是有限型的，拥有248种对称性操作。将 $E_8$ 这块瓷砖无限平铺，会得到仿射型的 $E_9$ ，它拥有无限个生成元，但其结构具有周期性。如果铺到双曲曲面上，就会得到 $E_{10}$ ，它的无限生成元不再有简单的周期性，其结构以指数级速度变得复杂，充满了混沌的色彩。

它的根格存在于一个10维（一个时间维度，九个空间维度）闵可夫斯空间中。一个由 $E_{10}$ 对称性所定义的、拥有无限维度的双曲空间。这个空间的边界由 $E_{10}$ 的根向量精确定义，它们代表了所有可能的对称性变换。宇宙的完整状态被编码为这个无限维空间中的一个点。时间的流逝，就是宇宙泡在这个双曲空间中沿着测地线运动的过程。

随着时间趋近于大爆炸奇点，这个宇宙泡会疯狂地、永无休止地与边界的墙壁发生碰撞。每一次碰撞，都对应着一次剧烈的物理事件。与引力墙碰撞会改变时空几何的性质。某个空间维度可能从收缩状态猛然转变为膨胀状态，而另一个维度则相反。这被称为 BKL 振荡，是广义相对论在奇点附近的混沌行为。

与物质墙碰撞，会激活或改变某种物质场。一次碰撞可能凭空激发出电磁场，下一次碰撞又可能将其关闭，转而生成别的场。在这个模型中，我们熟知的 3+1 维时空和标准模型的粒子，都只是这场无限碰撞的桌球游戏暂时激活的、极少数的自由度。绝大多数时候，宇宙处于一个维度疯狂涨落、场不断生灭的混沌状态。

如果说 $E_{10}$ 是试图描绘宇宙的创世书，那么 $E_{11}$ 的野心则更为宏大。它试图成为多元宇宙的创造之书。M理论是目前统一所有五种超弦理论和11维超引力的终极理论框架，但我们对它的数学原理知之甚少。物理学家 Peter West 等人提出， $E_{11}$ 可能就是我们苦苦追寻的M理论的数学骨架。

与 $E_{10}$ 类似， $E_{11}$ 也是一个通过扩展 $E_8$ 得到的双曲型卡茨-穆迪代数，但它定义在一个11维的洛伦兹空间中。它比 $E_{10}$ 更为庞大和复杂。 $E_{11}$ 猜想认为，物理学的一切都可以从这个单一的代数结构中涌现出来。在 $E_{11}$ 代数中，其无限的生成元被分成了不同的层级。

0级生成元：对应着11维超引力的对称性，包括引力子以及时空度规
更高级的生成元：预言了无穷无尽的、新的高阶张量场。

这意味着，我们不再需要像标准模型那样手动添加各种粒子。所有已知的和未知的基本粒子，都只是 $E_{11}$ 这个单一对称性结构的不同振动模式而已。在 $E_{11}$ 框架中，时空不再是预先给定的背景舞台。相反，11维时空的坐标 $(x^0, x^1, \dots, x^{10})$ 本身，就是与 $E_{11}$ 代数的某些生成元相关联的。

时空维度是从代数结构中生长出来的。我们熟悉的3+1维世界，很可能是 $E_{11}$ 这个庞大对称性在宇宙演化过程中自发破缺后，所剩下的一个稳定的低能子结构。

物理学的核心是动力学方程，比如我们熟知的麦克斯韦方程组、爱因斯坦场方程。在 $E_{11}$ 猜想中，我们甚至不需要再额外书写这些方程。 $E_{11}$ 代数的定义关系本身，就包含了所有的动力学信息，两个场的相互作用，被编码为它们对应生成元的李括号。一个场的演化，则由它与其他所有生成元的代数关系所决定。

Kac-Moody 代数告诉我们，宇宙的终极奥秘，可能不是隐藏在一组复杂的偏微分方程中，而是蕴含在一个单一、完美而无限的对称性结构之内。对物理现实的探索，最终将成为对这个终极数学结构的探索，无论是 $E_{10}$ 、 $E_{11}$ 还是别的什么。

Borcherds 代数

在我们之前对对称性的追寻中，我们已经习惯了一种自底向上构建的思维模式：从点到线，从有限到无限。 $SU(3)$ 是有限的，仿射卡茨-穆迪代数是无限周期的，而 $E_{10}$ 则是无限且混沌的。它们都遵循着一套相对刚性的生成规则。

在20世纪70年代末，数学界出现了一个令人匪夷所思的谜题，它将两个看似风马牛不相及的领域硬生生地拉到了一起。这个谜题，就是著名的魔群月光猜想（Monstrous Moonshine Conjecture）。

在纯数学中有一类被称为有限单群的存在，它们是构成所有有限对称性的原子。经过长达一个世纪的艰苦努力，数学家们终于在20世纪末完成了对它们的完整分类。这个分类名录包含了18个无限家族和26个零星散落的散在单群（Sporadic Groups）。

这些散在群是真正的数学怪胎，它们不属于任何规则的家族，其中最大、最复杂的一个，被称为魔群（Monster Group, $\mathbb{M}$ ）。魔群是一个有限的对称操作集合，但其元素的数量大到超乎想象：

|\mathbb{M}| \approx 8 \times 10^{53}

这个数字比地球上的沙粒数量还要多得多。它还拥有194个不同的不可约表示。它是一个结构极其复杂，但又完美自洽的有限对称性实体。

另外一群数学家在复分析和数论中，发现一个核心函数，叫做克莱因 $j$ -不变量（Klein’s j-invariant），记作 $j(\tau)$ 。

$j(\tau)$ 是一个模形式（Modular Form），他是一个定义在复平面上的、具有极高对称性的函数。当它的变量 $\tau$ 经过某些特定的分数线性变换时，函数值保持不变。令人物理学家惊讶的是，当一个弦在24个空间维度中传播时，其量子涨落的分配方式就与 $j(\tau)$ 直接相关。

1978年，数学家约翰·麦凯（John McKay）注意到：

j(\tau) = \frac{1}{q} + 744 + 196884q + 21493760q^2 + \dots \quad (\text{\small 其中 } q=e^{2\pi i \tau})

他发现，第一个非平凡系数 196884，竟然等于魔群 $\mathbb{M}$ 两个最简单的不可约表示的维度之和： $196884 = 196883 + 1$ ，而且接下来的系数也同样是魔群表示维度的简单线性组合。

这个发现震惊了数学界。一个来自离散代数的、极其庞大的有限魔群，其内在属性竟然被一个来自复分析和弦论的连续函数 $j(\tau)$ 的展开系数所精确编码？这太不可思议了，仿佛晚上喝多了胡言乱语一般，因此得名“模群月光猜想”。

如何解释这种魔幻的联系？常规的李代数或卡茨-穆迪代数都对此无能为力。它们要么是有限的，要么是无限的，但它们的结构都过于规整，无法容纳像魔群这样奇特的对称性。

这时，英国数学家理查德·博赫兹（Richard Borcherds）创造了一种对卡茨-穆迪代数更大胆的推广，如今被称为博赫兹代数（Borcherds Algebras）。核心思想在于允许代数的单根中包含虚根。

在传统的李代数和卡茨-穆迪代数中，所有的单根都是实的，意味着它们自身的长度平方为正。它们作为刚性的骨架，每一个都对应代数中的一个维度。博赫兹允许一些单根是类光甚至类时的，其自身长度平方为零或负。这些虚根不再像刚性的骨架一样代表维度，而更像是一种场或振动模式。

一个虚根不再仅仅增加一个维度，而是可以一次性引入一整族无限多个维度。这种引入虚根的做法，赋予了代数结构前所未有的灵活性和包容性。利用这种新的强大工具，博赫兹最终在1992年证明了魔群月光猜想。

他的证明过程堪称神来之笔：他构造了一个特殊的、无限维的博赫兹代数，其结构与弦论的世界面理论紧密相关。他证明了，这个庞大而复杂的无限维代数，其完整的对称群，不多不少，正好就是魔群 $\mathbb{M}$ 。最关键的一步在于，他推导出了一个描述这个怪物结构的公式，而这个公式的分母部分，精确地等于 $j(\tau) - 744$ 。

另一方面物理学家知道，26维玻色子弦论是最简单的一种弦论模型。为了保证量子力学上的自洽性，消除一种称为反常效应，这种理论必须生活在26个时空维度中。弦在时空中传播时，其轨迹形成一个二维的世界面（Worldsheet）。描述这个世界面上物理规律的数学语言，就是二维共形场论（2D CFT）。

在量子理论中，配分函数加总了一个系统所有可能存在的量子态。对于弦论来说，配分函数 $Z$ 就记录了弦在不同能量下所有可能的振动模式。当物理学家计算一个在26维时空中传播的弦，并将其中的24个空间维紧致化在一个极其特殊的、名为利奇格（Leech Lattice）的24维点阵上时，他们得到的配分函数 $Z(\tau)$ ，不多不少，正好就是：

Z(\tau) = j(\tau) - 744

这个结果石破天惊，它意味着：

j(\tau) = \frac{1}{q} + 744 + \mathbf{196884}q + \mathbf{21493760}q^2 + \dots

展开式中的每一个系数，都有了明确的物理意义！

系数196884，不再仅仅是魔群两个表示的维度和，它现在代表了在这个特定弦论模型中，处于第一个激发能级的所有可能的量子态的总数。同样，下一个系数 21493760 则代表了第二个激发能级的所有量子态的总数。

于是，整个谜题的逻辑链条完整了：

魔群( $\mathbb{M}$ ) $\longleftrightarrow$ 魔幻李代数 $\longleftrightarrow$ $j(\tau)$ 函数 $\longleftrightarrow$ 26维弦论的配分函数

魔幻李代数，正是描述这个特定26维弦论模型所有量子态的内在代数结构。而魔群，就是这个弦论态空间的完整对称群。这个理论被称为魔幻共形场论（Monster CFT）。它不仅仅是数学上的一个虚构的理论，而是物理上一个真实存在的、自洽的理论模型。

至此，谜底揭晓。魔群与 $j$ -不变量的联系并非巧合，而是因果：

魔群是某个特定博赫兹代数的对称群，而这个代数的结构本身，又自然地生成了 $j$ -不变量。它们是同一个深层数学实体在不同视角下的投影。

博赫兹代数和月光猜想的证明，为我们揭示了一种全新的、关于宇宙秩序的深刻见解：魔群本身结构复杂到近乎混沌，但它却是一个高度有序的有限实体。它所支配的“魔群代数”是一个无限维的、看似更加混沌的结构。然而，这种混沌背后存在着由虚根和模形式支配的精妙规则。

这是一次在离散数学、连续数学和理论物理之间联合作战。它暗示我们，宇宙中看似分离的法则可能在更深的层次上是统一的。宇宙的基本构件，除了我们熟知的点状粒子（对应实根），可能还包括某些弥散的、场状的基本激发（对应虚根）。对称性的世界远比我们想象的更加广阔和奇妙。

魔幻共形场论本身是一个二维理论，但它可能与更高维度的物理，特别是引力，有着深刻的联系。这主要体现在对一种简化的2+1维量子引力的研究中。爱德华·威滕（Edward Witten）等物理学家提出的一个猜想认为：

魔幻共形场论可能是一个特定的三维量子引力理论的全息对。

如果这个猜若是正确的，那么三维时空中的BTZ黑洞，其熵的计算结果，可以与怪兽CFT中量子态的数量精确对应。

这意味着，魔群这个庞大的对称性，可能正是支配这些黑洞量子微观态的根本法则。黑洞不再是一个光滑的几何天体，而是一个由 $8 \times 10^{53}$ 种对称性操作所支配的、极其复杂的量子系统。通过研究魔群的代数结构，或许就能揭开量子引力与黑洞信息之谜的一角。

弦论并非单一理论，而是包含着无数可能解的广阔景观（Landscape）。每一个解都对应一个可能的宇宙。在这个浩瀚的景观中，魔幻共形场论显得极其特殊和孤独。它具有极高的对称性和完美的数学自洽性，理论物理学家进入贤者时间后又开始胡乱思考：

为什么宇宙的数学法则允许这样一个点的存在？
它是否在所有可能的物理理论中占据了一个基础性的地位？
我们所处的四维宇宙，有没有可能是在宇宙大爆炸早期，从这样一个高度对称的魔幻状态，通过对称性破缺演化而来的？

这些发现强烈地暗示了数学的内在结构与物理的现实法则之间，可能存在着一种我们尚未完全理解的、必然的联系。宇宙的法则，或许就是从最深刻的数学结构中涌现出来的。

范畴对称性

我们对对称性的理解发生了一次又一次的的飞跃，然而，这样高屋建瓴的理解仍然称不上现代。在此之前，我们讨论的对称性，无论是旋转一个正方形，还是在每个时空点进行一次相位变换，其主角始终是对象本身。一个晶体、一个波函数、一个物理系统。现在，我们要将目光从对象移开，投向一个更抽象关系。我们不再只关注单个星球的运动，而是开始描绘整个星系中所有星体之间的引力关系图谱。

当我们将焦点从事物转向事物之间的联系时，对称性的概念也随之升华。这种革命的数学语言，就是范畴论（Category Theory）。范畴论被戏称为抽象废话，因为它几乎剥离了所有具体内容，只专注于研究结构与关系的纯粹形式。它为我们提供了一张终极的蓝图，去描绘不同数学乃至物理世界之间是如何相互连接和转换的。

一个范畴由两个基本元素构成：

对象（Objects）：一个对象可以是一个集合、一个几何空间、一个群，甚至可以是另一个范畴。
态射（Morphisms）：一个态射描述了从一个对象到另一个对象的关系。例如，集合之间的函数、拓扑空间之间的连续映射、群之间的同态，都是态射。

这些态射的组合必须满足一些简单的规则，比如箭头的连接是可结合的，并且每个对象都有一个指向自身的什么都不做的单位态射。

在物理学中，系统和过程天然地构成了范畴。在一个量子系统中，不同的量子态可以被看作是对象。而使系统从一个态演化到另一个态的量子过程或者时间演化算符 $e^{-iHt/\hbar}$ ，就是态射。整个量子力学的动力学过程，都可以被看作是在一个巨大的量子态范畴中，沿着不同的箭头进行演化。

范畴论的威力在高阶范畴中被发挥到了极致。普通范畴研究的是对象和对象间的关系，这被称为 1-态射。高阶范畴则引入了：

2-态射：关系与关系之间的关系
3-态射：关系与关系之间关系的关系
…直至无限。

这多少有点抽象，但它完美地捕捉了物理世界中过程的嵌套性。

0-态射：一个粒子
1-态射：粒子从A点运动到B点的世界线
2-态射：将一条世界线连续变形成另一条世界线的过程的过程

这在费曼的路径积分中体现得淋漓尽致，物理学家需要加总所有可能的路径，而这些路径之间是可以相互变形的。

高阶范畴在爱德华·威滕等人发展的拓扑量子场论（TQFT）中找到了用武之地。TQFT是一种特殊的量子场论，其计算结果不依赖于时空的具体几何形状，如距离和角度。其计算只依赖于其拓扑结构，比如时空如何连接和扭曲。

一个 $n$ 维的TQFT，其数学结构就是一个从几何范畴到代数范畴的称为函子，它将一个(n-1)维空间赋予一个代数对象。又将一个连接两个(n-1)维空间的n维管道赋予一个代数态射。这种对应关系是如此的完美，以至于可以说，高阶范畴就是TQFT的母语。它揭示了一种深刻的关系对称：

物理定律本身的代数结构反映了几何时空的拓扑结构。

拓扑斯范畴

在范畴论的大家族中，有一类被称为拓扑斯（Topos）的特殊范畴。每一个拓扑斯都像是一个自给自足、逻辑完备的数学宇宙。它内部包含了自己版本的集合论，并遵循着自己的一套内部逻辑。拓扑斯的内部逻辑不一定是我们日常熟悉的经典逻辑。

在经典逻辑中，任何一个命题 $P$ 要么为真，要么为假，这被称为排中律。但在许多拓扑斯中，排中律并不成立！它们的逻辑是构造性逻辑，一个命题只有在你能构造出它的证明时才被认为是真的。

这一特性立刻引起了研究量子引力的物理学家的注意。量子力学的核心特征叠加原理天生就与经典逻辑相悖。一个电子在被测量前，说“它在自旋向上”是假的，说“它不在自旋向上”也是假的。它处于一种“向上”和“向下”的叠加态， “电子自旋向上或电子自旋不向上”这个排中律在这里失效了。

物理学家克里斯·伊沙姆（Chris Isham）等人提出，描述量子引力世界的正确数学框架，可能不是我们熟悉的希尔伯特空间，而是一个拓扑斯。在这个框架中，物理量不再由简单的数值表示，而是由拓扑斯内部的对象来表示。我们关于这个世界的命题，其真值不再是简单的{真, 假}二元集合，而是拓扑斯内部一个更复杂的真值对象。

整个量子世界的诡异行为，或许只是因为我们试图用经典的、二值的逻辑去理解一个本质上是构造性的、多值的拓扑斯宇宙。这里的对称性已经升华到了逻辑的对称性：

经典力学和量子力学，不同的物理理论可以被看作是生活在具有不同内部逻辑的拓扑斯中。而连接这些拓扑斯的几何态射，则揭示了不同物理现实之间深刻的逻辑变换关系。

$\infty$ -范畴

现在，我们抵达了这条路的顶峰。将高阶范畴的阶数推向无穷，我们得到了 $\infty$ -范畴。这是一个包含了无限层级对象、态射、2-态射……的终极数学结构，由雅各布·卢里（Jacob Lurie）等数学家系统地建立起来。 $\infty$ -范畴拥有难以想象的丰富性和复杂性，但它也提供了前所未有的统一能力。

许多前沿物理学家对此有着深入地研究，他们认为M理论的景象远比点粒子复杂：基本对象不再只是点，还包括弦（1维）、膜（高维 D-branes）等。这些对象之间的相互作用也极其复杂：一根开弦可以连接两个D膜，D膜之间可以碰撞等。而 $\infty$ -范畴为这个复杂的物理现象动物园提供了一个完美的组织框架：

0-态射：各种D膜。
1-态射：在膜之间拉伸的弦。
2-态射：弦与弦之间的相互作用。
更高态射：更复杂的未知动力学过程……

在这个视图下，我们之前章节讨论的所有对称性，包括标准模型的 $SU(3) \times SU(2) \times U(1)$ 规范对称性，都可能只是某个巨大的、底层的 $\infty$ -范畴对称性在一个低能量角落的粗糙投影。

这个终极的对称性不再是关于变换一个物体使其保持不变，而是关于整个物理理论的所有可能的过程、所有可能的形变、以及所有可能的逻辑表述之间，如何以一种和谐、自洽的方式相互关联。它是一种关于存在本身所有可能性的终极对称性。

从研究物体的几何对称，到研究关系的代数对称，再到研究逻辑本身的构造对称，范畴论将我们带到了一个前所未有的高度。宇宙的终极法则，或许并非写在一块坚硬的石板上，而是编织在一张由无限层级关系构成的、动态而柔韧的巨网之中。

我们现在抵达了现代对称性的最高峰，一个真正将逻辑、数学和物理现实融为一体的领域。不过，我们对对称性的理解或许还可以经历一次终极的升华，触及存在与相等这些概念最根本的核心。

同伦类型论

在穿越了范畴论的抽象废话垃圾场后，我们似乎来到了一个思想的奇点。在这里，各种看似永不相交的理论以一种出人意料的方式汇聚在一起。它们的交汇点，形成了一片名为同伦类型论（Homotopy Type Theory, HoTT）新落脚点。

HoTT不仅是一种新的数学理论，它更像是一种全新的世界观。它提出了一种革命性的思想，彻底重塑了我们对最基本概念相等的理解。

相等即路径（Equality is Homotopy）

在两千多年的数学传统中，相等（ $A=B$ ）是一个不容置疑的绝对真理。它是一个二元命题，要么为真，要么为假，不存在中间状态。而 HoTT宣称：

相等不是一个状态，而是一个过程；相等即路径。

传统数学中的相等，问“A点和B点相等吗？” 只有在A和B是同一个重合的点时，答案才是是。HoTT中的相等，问“A点和B点相等吗？”答案是：“如果存在一条从A到B的连续路径，那么是的。”这个路径本身在数学上称为同伦（Homotopy），它是被视为“相等”的证明，相等不再是静态的逻辑断言，而是一个动态的、可构造的证据。

相等是有结构的，既然相等是一条路径，那么从A到B可能存在多条不同的路径。这些路径本身又可以相互形变，这就引出了路径之间的路径，也就是 2-同伦，乃至无穷层级的同伦结构。一个对象自相等（ $A=A$ ）也不再是无意义的同义反复，它变成了一个从A出发又回到A的环路（Loop）。这个对象所有的环路结构，正是在拓扑学中描述其洞和形状的同伦群。

一个球体旋转 360度后回到原位，和它完全不动，在HoTT 视角下是相等的。因为存在一个旋转过程，连接了初始状态和最终状态。这个旋转路径本身，就是这两个状态相等的证明。这种路径连续可变形性，就是一种内在于时空与对象本身的动态对称性。

由数学家弗拉基米尔·沃埃沃德斯基（Vladimir Voevodsky）等人开创的 HoTT，其目标是为数学建立一个全新的合一基础（Univalent Foundations）。在这个基础之上，一个数学对象的是什么，和它如何运动是同一件事。

在量子世界，一个粒子从A点到B点，它并不会选择一条确定的轨迹。相反，它会同时探索所有可能的路径。最终的概率幅，是所有这些路径贡献的叠加和干涉。粒子所有可能存在的位置即为存在，粒子从A到B的每一条费曼历史路径即为同伦。

爱因斯坦的广义相对论将引力描述为时空的弯曲。一个在引力场中自由运动的物体，会沿着时空中最的路径测地线运动。引力的本质，就是对路径概念的扭曲。平直时空，从A到B的直线路径是唯一的。弯曲时空，由于引力的存在，从A到B的测地线可能不再唯一，一个矢量沿着一条闭合环路运动回来后，会发生和乐（Holonomy）。引力场可以被完全理解为时空这个存在中环路空间（Loop Space）的非平凡结构。时空的曲率张量 $R_{\mu\nu\rho\sigma}$ 本质上就是对无穷小的环路路径行为的数学描述。而引力则被重新诠释为时空本身的同伦性质。

规范对称性是说我们可以在每个时空点独立地“旋转”我们的数学描述标尺，而物理定律不变。这是一种描述上的相等性。一次规范变换连接了两个在数学上不同，但在物理上完全等价的场构型。规范场论等于是说，物理学并非由单一的场构型决定，而是由所有通过规范变换这条路径连接起来的等价类所决定。如瞬子（Instantons）正是对应了规范场构型空间中那些无法被连续形变缩为一点的非平凡环路。它们是物理真空的同伦洞（Homotopy Hole），直接导致了奇异的物理效应。

HoTT 为我们描绘了一种玄妙的终极物理图景。它不仅仅是为物理学提供了一个更好用的数学工具，它在暗示一件更深刻的事情：

物理定律的结构和数学逻辑的结构，可能是同构的。

一个物理可能性就是一种存在，一个物理过程就是一条路径。

不同的过程可以导致相同的宏观结果，它们之间是物理等价的。此即同伦。同伦论告诉我们，宇宙最深层的对称性，或许既不是几何的，也不是代数的，而是一种逻辑的、动态的、关于关系与变化本身的规律。

宇宙之所以如此运行，或许只是因为它在遵循一套内在自洽的、以等价为核心的同伦逻辑。在这种图景下，现实世界本身，就是其自身最深刻、最完美的证明。